Десятичной дроби число стоящее. Десятичные дроби и действия с ними

дробного числа.

Десятичная запись дробного числа представляет собой набор двух и более цифр от $0$ до $9$, между которыми находится так называемая \textit{десятичная запятая}.

Пример 1

Например, $35,02$; $100,7$; $123 \ 456,5$; $54,89$.

Крайняя левая цифра в десятичной записи числа не может быть нулем, исключением является только случай, когда десятичная запятая стоит сразу после первой цифры $0$.

Пример 2

Например, $0,357$; $0,064$.

Часто десятичную запятую заменяют десятичной точкой. Например, $35.02$; $100.7$; $123 \ 456.5$; $54.89$.

Определение десятичной дроби

Определение 1

Десятичные дроби -- это дробные числа, которые представлены в десятичной записи.

Например, $121,05$; $67,9$; $345,6700$.

Десятичные дроби используются для более компактной записи правильных обыкновенных дробей, знаменателями которых являются числа $10$, $100$, $1 \ 000$ и т.д. и смешанные числа, знаменателями дробной части которых являются числа $10$, $100$, $1 \ 000$ и т.д.

Например, обыкновенную дробь $\frac{8}{10}$ можно записать в виде десятичной дроби $0,8$, а смешанное число $405\frac{8}{100}$ -- в виде десятичной дроби $405,08$.

Чтение десятичных дробей

Десятичные дроби, которые соответствуют правильным обыкновенным дробям , читаются также как и обыкновенные дроби, только впереди добавляется фраза «ноль целых». Например, обыкновенной дроби $\frac{25}{100}$ (читается «двадцать пять сотых») отвечает десятичная дробь $0,25$ (читается «нуль целых двадцать пять сотых»).

Десятичные дроби, которые соответствуют смешанным числам, читаются также как и смешанные числа. Например, смешанному числу $43\frac{15}{1000}$ соответствует десятичная дробь $43,015$ (читается «сорок три целых пятнадцать тысячных»).

Разряды в десятичных дробях

В записи десятичной дроби значение каждой цифры зависит от ее позиции. Т.е. в десятичных дробях также имеет место понятие разряда .

Разряды в десятичных дробях до десятичной запятой называются так же, как и разряды в натуральных числах. Разряды в десятичных дробях после запятой вынесены в таблицу:

Рисунок 1.

Пример 3

Например, в десятичной дроби $56,328$ цифра $5$ стоит в разряде десятков, $6$ - в разряде единиц, $3$ - в разряде десятых, $2$ - в разряде сотых, $8$ -- в разряде тысячных.

Разряды в десятичных дробях различают по старшинству. При чтении десятичной дроби движутся слева направо -- от старшего разряда к младшему .

Пример 4

Например, в десятичной дроби $56,328$ старшим (высшим) разрядом является разряд десятков, а младшим (низшим) -- разряд тысячных.

Десятичную дробь можно разложить по разрядам аналогично разложению по разрядам натурального числа.

Пример 5

Например, разложим по разрядам десятичную дробь $37,851$:

$37,851=30+7+0,8+0,05+0,001$

Конечные десятичные дроби

Определение 2

Конечными десятичными дробями называют десятичные дроби, в записях которых содержится конечное число знаков (цифр).

Например, $0,138$; $5,34$; $56,123456$; $350 972,54$.

Любую конечную десятичную дробь можно перевести в обыкновенную дробь или смешанное число.

Пример 6

Например, конечной десятичной дроби $7,39$ отвечает дробное число $7\frac{39}{100}$, а конечной десятичной дроби $0,5$ соответствует правильная обыкновенная дробь $\frac{5}{10}$ (или любая дробь, которая равна ей, например, $\frac{1}{2}$ или $\frac{10}{20}$.

Перевод обыкновенной дроби в десятичную дробь

Перевод обыкновенных дробей со знаменателями $10, 100, \dots$ в десятичные дроби

Перед переводом некоторых правильных обыкновенных дробей в десятичные их нужно предварительно «подготовить». Результатом такой подготовки должно быть одинаковое количество цифр в числителе и количество нулей в знаменателе.

Суть «предварительной подготовки» правильных обыкновенных дробей к переводу в десятичные дроби -- дописывание слева в числителе такого числа нулей, чтобы общее количество цифр стало равно числу нулей в знаменателе.

Пример 7

Например, подготовим обыкновенную дробь $\frac{43}{1000}$ к переводу в десятичную и получим $\frac{043}{1000}$. А обыкновенная дробь $\frac{83}{100}$ в подготовке не нуждается.

Сформулируем правило перевода правильной обыкновенной дроби со знаменателем $10$, или $100$, или $1 \ 000$, $\dots$ в десятичную дробь :

записать $0$;

после него поставить десятичную запятую;

записать число из числителя (вместе с дописанными нулями после подготовки, если она была нужна).

Пример 8

Перевести правильную обыкновенную дробь $\frac{23}{100}$ в десятичную.

Решение.

В знаменателе стоит число $100$, которое содержит $2$ два нуля. В числителе стоит число $23$, в записи которого $2$.цифры. значит, подготовку для этой дроби к переводу в десятичную проводить не нужно.

Запишем $0$, поставим десятичную запятую и запишем число $23$ из числителя. Получим десятичную дробь $0,23$.

Ответ : $0,23$.

Пример 9

Записать правильную дробь $\frac{351}{100000}$ в виде десятичной дроби.

Решение.

В числителе данной дроби $3$ цифры, а число нулей в знаменателе -- $5$, поэтому данную обыкновенную дробь нужно подготовить к переводу в десятичную. Для этого необходимо дописать $5-3=2$ нуля слева в числителе: $\frac{00351}{100000}$.

Теперь можем составить нужную десятичную дробь. Для этого запишем $0$, затем поставим запятую и запишем число из числителя. Получим десятичную дробь $0,00351$.

Ответ : $0,00351$.

Сформулируем правило перевода неправильных обыкновенных дробей со знаменателями $10$, $100$, $\dots$ в десятичные дроби :

записать число из числителя;

отделить десятичной запятой столько цифр справа, сколько нулей в знаменателе исходной дроби.

Пример 10

Перевести неправильную обыкновенную дробь $\frac{12756}{100}$ в десятичную дробь.

Решение.

Запишем число из числителя $12756$, затем отделим десятичной запятой $2$ цифры справа, т.к. в знаменателе исходной дроби $2$ нуля. Получим десятичную дробь $127,56$.

В данной статье мы с Вами разберемся, что такое десятичная дробь, какие у нее есть особенности и свойства. Поехали! 🙂

Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).

Определение

Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.

Примеры дробей:

, ,

Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.

Представление дроби в десятичной записи

В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:

где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.

Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).

Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.

Пример:

Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.

В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.

Прочтение десятичных дробей

Часть Х читается в общем случае так: «Х целых».

Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉

Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.

Наименования для правильного прочтения приведены в таблице:

Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.

3,5 читается как «три целых пять десятых»
0,016 читается как «ноль целых шестнадцать тысячных»

Перевод произвольной обыкновенной дроби в десятичную

Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.

Существует 2 способа перевода.

Первый способ перевода

Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.

Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере . Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.

Второй способ перевода

2-й способ заключается в делении числителя на знаменатель в столбик или на калькуляторе. Целая часть, если таковая имеется, в преобразовании не участвует.

Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).

Перевод десятичной дроби в обыкновенную

Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.

Конечная и бесконечная десятичная дробь

Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.

Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.

В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:

как результат сокращения до желательного количества разрядов после запятой;
в виде периодической дроби.

Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.

Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).

Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби .

Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.

54,33333… – периодическая чистая десят.дробь

2,5621212121… – периодическая смешанная дробь

Примеры записи бесконечных десятичных дробей:

Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.

Перевод периодических десятичных дробей в обыкновенные

Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.

Смешанная периодическая десятичная дробь переводится следующим образом:

нужно сформировать число, состоящее из числа, стоящего после запятой до периода, и первого периода;
из полученного числа вычесть число, стоящее после запятой до периода. Итог составит числитель обыкновенной дроби;
в знаменателе требуется вписать число, состоящее из кол-ва девяток, равных кол-ву цифр периода, а за ними нулей, кол-во которых равно количеству цифр числа, стоящего после запятой до 1-го периода.

Сравнение десятичных дробей

Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.

Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.

Поскольку

, поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.

Сложение и вычитание десятичных дробей

Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.

Умножение десятичных дробей

Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.

Умножение и деление десятичных дробей на 10 n

Эти действия просты и сводятся к переносу десятичной запятой. При умножении запятая переносится вправо (дробь увеличивается) на количество знаков, равных количеству нулей в 10 n , где n – произвольная целая степень. То есть некоторое количество цифр переносится из дробной части в целую. При делении, соответственно, запятая переносится влево (число уменьшается), и некоторая часть цифр переносится из целой части в дробную. Если цифр для переноса оказывается недостаточно, то недостающие разряды заполняются нулями.

Деление десятичной дроби и целого числа на целое число и на десятичную дробь

Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.

Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.

Для деления десят.дроби (или целого числа) на десят.число необходимо домножить делимое и делитель на число 10 n , в котором количество нулей равно количеству цифр после десят.запятой в делителе. Таким способом избавляются от десят.запятой в дроби, на которую требуется делить. Далее процесс деления совпадает с описанным выше.

Графическое представление десятичных дробей

Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.

Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.

Десятичные дроби - это те же самые обыкновенные дроби, но в так называемой десятичной записи. Десятичная запись используется для дробей со знаменателями 10, 100, 1000 и т. д. При этом вместо дробей 1/10; 1/100; 1/1000; ... пишут 0,1; 0,01; 0,001;... .

К примеру, 0,7 (ноль целых семь десятых ) - это дробь 7/10; 5,43 (пять целых сорок три сотых ) - это смешанная дробь 5 43/100 (или, что то же самое, неправильная дробь 543/100).

Может случиться так, что сразу после запятой стоит один или несколько нулей: 1,03 - это дробь 1 3/100; 17,0087 - это дробь 17 87/10000. Общее правило таково: в знаменателе обыкновенной дроби должно быть столько нулей, сколько цифр стоит после запятой в записи десятичной дроби .

Десятичная дробь может оканчиваться на один или несколько нулей. Оказывается, эти нули «лишние» - их можно попросту убрать: 1,30 = 1,3; 5,4600 = 5,46; 3,000 = 3. Сообрази, почему это так?

Десятичные дроби естественным образом возникают при делении на «круглые» числа - 10, 100, 1000, ... Обязательно разберись в следующих примерах:

27:10 = 27/10 = 2 7/10 = 2,7;

579:100 = 579/100 = 5 79/100 = 5,79;

33791:1000 = 33791/1000 = 33 791/1000 = 33,791;

34,9:10 = 349/10:10 = 349/100 = 3,49;

6,35:100 = 635/100:100 = 635/10000 = 0,0635.

Замечаешь ли ты здесь некую закономерность? Попробуй ее сформулировать. А что будет, если умножить десятичную дробь на 10, 100, 1000?

Чтобы перевести обыкновенную дробь в десятичную, нужно привести ее к какому-нибудь «круглому» знаменателю:

2/5 = 4/10 = 0,4; 11/20 = 55/100 = 0,55; 9/2 = 45/10 = 4,5 и т. д.

Складывать десятичные дроби намного удобнее, чем дроби обыкновенные. Сложение производится так же, как и с обычными числами - по соответствующим разрядам. При сложении в столбик слагаемые нужно записывать так, чтобы их запятые находились на одной вертикали. На этой же вертикали окажется и запятая суммы. Совершенно аналогично выполняется и вычитание десятичных дробей.

Если при сложении или вычитании в одной из дробей количество цифр после запятой меньше, чем в другой, то в конце данной дроби следует дописать нужное число нулей. Можно эти нули и не дописывать, а просто представить их себе в уме.

При умножении десятичных дробей их опять-таки следует перемножить как обычные числа (при этом уже не обязательно записывать запятую под запятой). В полученном результате нужно отделить запятой количество знаков, равное суммарному числу знаков после запятой в обоих множителях.

При делении десятичных дробей можно в делимом и делителе одновременно передвинуть запятую вправо на одно и то же количество знаков: частное от этого не изменится:

2,8:1,4 = 2,8/1,4 = 28/14 = 2;

4,2:0,7 = 4,2/0,7 = 42/7 = 6;

6:1,2 = 6,0/1,2 = 60/12 = 5.

Объясни, почему это так?

Нарисуй квадрат 10x10. Закрась какую-нибудь его часть, равную: а) 0,02; б) 0,7; в) 0,57; г) 0,91; д) 0,135 площади всего квадрата.
Что такое 2,43 квадрата? Изобрази на рисунке.
Раздели на 10 числа 37; 795; 4; 2,3; 65,27; 0,48 и результат запиши в виде десятичной дроби. Эти же числа раздели на 100 и на 1000.
Умножь на 10 числа 4,6; 6,52; 23,095; 0,01999. Эти же числа умножь на 100 и на 1000.
Представь десятичную дробь в виде обыкновенной дроби и сократи ее:
а) 0,5; 0,2; 0,4; 0,6; 0,8;
б) 0,25; 0,75; 0,05; 0,35; 0,025;
в) 0,125; 0,375; 0,625; 0,875;
г) 0,44; 0,26; 0,92; 0,78; 0,666; 0,848.
Представь в виде смешанной дроби: 1,5; 3,2; 6,6; 2,25; 10,75; 4,125; 23,005; 7,0125.
Представь обыкновенную дробь в виде десятичной дроби:
а) 1/2; 3/2; 7/2; 15/2; 1/5; 3/5; 4/5; 18/5;
б) 1/4; 3/4; 5/4; 19/4; 1/20; 7/20; 49/20; 1/25; 13/25; 77/25; 1/50; 17/50; 137/50;
в) 1/8; 3/8; 5/8; 7/8; 11/8; 125/8; 1/16; 5/16; 9/16; 23/16;
г) 1/500; 3/250; 71/200; 9/125; 27/2500; 1999/2000.
Найди сумму: а) 7,3+12,8; б) 65,14+49,76; в) 3,762+12,85; г) 85,4+129,756; д) 1,44+2,56.
Представь единицу в виде суммы двух десятичных дробей. Найди еще двадцать способов такого представления.
Найди разность: а) 13,4–8,7; б) 74,52–27,04; в) 49,736–43,45; г) 127,24–93,883; д) 67–52,07; е) 35,24–34,9975.
Найди произведение: а) 7,6·3,8; б) 4,8·12,5; в) 2,39·7,4; г) 3,74·9,65.

В этом уроке мы рассмотрим каждую из этих операций по отдельности.

Содержание урока

Сложение десятичных дробей

Как мы знаем, десятичная дробь имеет целую и дробную часть. При сложении десятичных дробей, целые и дробные части складываются по отдельности.

Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.

Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .

Запишем дроби в столбик так, чтобы запятая оказалась под запятой:

Начинаем складывать дробные части: 2 + 3= 5. Записываем пятёрку в дробной части нашего ответа:

Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:

Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :

Получили ответ 8,5. Значит выражения 3,2 + 5,3 равно 8,5

На самом деле, не всё так просто, как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.

Разряды в десятичных дробях

У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.

Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.

Разряды в десятичных дробях хранят в себе некоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.

Например, рассмотрим десятичную дробь 0,345

Позиция, где находится тройка, называется разрядом десятых

Позиция, где находится четвёрка, называется разрядом сотых

Позиция, где находится пятёрка, называется разрядом тысячных

Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .

Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345

Видно, что сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.

При сложении десятичных дробей соблюдаются те же принципы и правила, что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.

Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.

Пример 1. Найти значение выражения 1,5 + 3,4

В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:

Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:

Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:

Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9

Пример 2. Найти значение выражения: 3,51 + 1,22

Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»

В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:

Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:

Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:

Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:

Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73

3,51 + 1,22 = 4,73

Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.

Пример 3. Найти значение выражения 2,65 + 3,27

Записываем в столбик данное выражение:

Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:

Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:

Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:

Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92

2,65 + 3,27 = 5,92

Пример 4. Найти значение выражения 9,5 + 2,8

Записываем в столбик данное выражение

Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:

Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3

9,5 + 2,8 = 12,3

При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.

Пример 5 . Найти значение выражения: 12,725 + 1,7

Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:

Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:

Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:

Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:

Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425

12,725+ 1,700 = 14,425

Вычитание десятичных дробей

При вычитании десятичных дробей нужно соблюдать те же правила, что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».

Пример 1. Найти значение выражения 2,5 − 2,2

Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:

Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:

Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3

2,5 − 2,2 = 0,3

Пример 2. Найти значение выражения 7,353 — 3,1

В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.

Теперь можно записать в столбик данное выражение и вычислить его:

Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253

7,353 — 3,1 = 4,253

Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.

Пример 3. Найти значение выражения 3,46 − 2,39

Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:

Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:

Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07

3,46−2,39=1,07

Пример 4 . Найти значение выражения 3−1,2

В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3

Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:

Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:

Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8

Умножение десятичных дробей

Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.

Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.

Пример 1. Найти значение выражения 2,5 × 1,5

Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:

Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.

Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75

2,5 × 1,5 = 3,75

Пример 2. Найти значение выражения 12,85 × 2,7

Перемножим эти десятичные дроби, не обращая внимания на запятые:

Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.

Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:

Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695

12,85 × 2,7 = 34,695

Умножение десятичной дроби на обычное число

Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.

Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.

Например, умножим 2,54 на 2

Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:

Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.

Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08

2,54 × 2 = 5,08

Умножение десятичных дробей на 10, 100, 1000

Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.

Например, умножим 2,88 на 10

Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:

Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.

Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8

2,88 × 10 = 28,8

Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.

Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.

2,88 × 10 = 28,8

Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288

2,88 × 100 = 288

Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.

2,88 × 1000 = 2880

Умножение десятичных дробей на 0,1 0,01 и 0,001

Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.

Например, умножим 3,25 на 0,1

Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:

Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.

Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:

Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325

3,25 × 0,1 = 0,325

Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.

Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325

3,25 × 0,1 = 0,325

Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325

3,25 × 0,01 = 0,0325

Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325

3,25 × 0,001 = 0,00325

Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.

При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.

А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.

Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.

Деление меньшего числа на большее. Продвинутый уровень.

В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.

Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»

Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.

Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.

При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.

Итак, разделим 1 на 2. Решим этот пример уголком:

Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:

Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:

Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:

Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:

Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10

Получили ответ 0,5. Значит дробь равна 0,5

Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:

Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см

Пример 2. Найти значение выражения 4: 5

Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:

Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.

Завершаем пример, умножив 8 на 5, и получив 40:

Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8

Пример 3. Найти значение выражения 5: 125

Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0

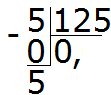
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:

Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0

Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50

Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:

Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:

Завершаем пример, умножив 4 на 125, и получив 500

Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04

Деление чисел без остатка

Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:

Допишем ноль к остатку 4

Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:

40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:

9: 5 = 1,8

Пример 2 . Разделить 84 на 5 без остатка

Сначала разделим 84 на 5 как обычно с остатком:

Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0

Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:

и завершаем пример, проверив есть ли еще остаток:

Деление десятичной дроби на обычное число

Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:

разделить целую часть десятичной дроби на это число;
после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.

Например, разделим 4,8 на 2

Запишем этот пример уголком:

Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:

Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:

4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2

8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:

Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4

Пример 2. Найти значение выражения 8,43: 3

Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:

Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:

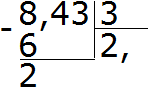
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:

24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:

Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81

Деление десятичной дроби на десятичную дробь

Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.

Например, разделим 5,95 на 1,7

Запишем уголком данное выражение

Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:

После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:

Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?

Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.

Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:

(9 × 2 ) : (3 × 2 ) = 18: 6 = 3

Как видно из примера, частное не поменялось.

Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.

На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:

5,91 × 10 = 59,1

Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.

Деление десятичной дроби на 10, 100, 1000

Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:

Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.

Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21

Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:

2,1: 100 = 0,021

Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:

2,1: 1000 = 0,0021

Деление десятичной дроби на 0,1, 0,01 и 0,001

Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.

Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.

После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:

Значит значение выражения 6,3: 0,1 равно 63

Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.

Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63

Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630

Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:

6,3: 0,001 = 6300

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Эта статья про десятичные дроби . Здесь мы разберемся с десятичной записью дробных чисел, введем понятие десятичной дроби и приведем примеры десятичных дробей. Дальше поговорим о разрядах десятичных дробей, дадим названия разрядов. После этого остановимся на бесконечных десятичных дробях, скажем о периодических и непериодических дробях. Дальше перечислим основные действия с десятичными дробями. В заключение установим положение десятичных дробей на координатном луче.

Навигация по странице.

Десятичная запись дробного числа

Чтение десятичных дробей

Скажем пару слов о правилах чтения десятичных дробей.

Десятичные дроби, которым соответствуют правильные обыкновенные дроби, читаются также как и эти обыкновенные дроби, только еще предварительно добавляется «ноль целых». Например, десятичной дроби 0,12 отвечает обыкновенная дробь 12/100 (читается «двенадцать сотых»), поэтому, 0,12 читается как «нуль целых двенадцать сотых».

Десятичные дроби, которым соответствуют смешанные числа, читаются абсолютно также как эти смешанные числа. Например, десятичной дроби 56,002 соответствует смешанное число , поэтому, десятичная дробь 56,002 читается как «пятьдесят шесть целых две тысячных».

Разряды в десятичных дробях

В записи десятичных дробей, также как и в записи натуральных чисел, значение каждой цифры зависит от ее позиции. Действительно, цифра 3 в десятичной дроби 0,3 означает три десятых, в десятичной дроби 0,0003 – три десяти тысячных, а в десятичной дроби 30 000,152 – три десятка тысяч. Таким образом, мы можем говорить о разрядах в десятичных дробях , так же как и о разрядах в натуральных числах .

Названия разрядов в десятичной дроби до десятичной запятой полностью совпадают с названиями разрядов в натуральных числах. А названия разрядов в десятичной дроби после запятой видны из следующей таблицы.

Например, в десятичной дроби 37,051 цифра 3 находится в разряде десятков, 7 – в разряде единиц, 0 стоит в разряде десятых, 5 – в разряде сотых, 1 – в разряде тысячных.

Разряды в десятичной дроби также различаются по старшинству. Если в записи десятичной дроби двигаться от цифры к цифре слева на право, то мы будем перемещаться от старших к младшим разрядам . Например, разряд сотен старше разряда десятых, а разряд миллионных младше разряда сотых. В данной конечной десятичной дроби можно говорить о старшем и младшем разряде. К примеру, в десятичной дроби 604,9387 старшим (высшим) разрядом является разряд сотен, а младшим (низшим) - разряд десятитысячных.

Для десятичных дробей имеет место разложение по разрядам. Оно аналогично разложению по разрядам натуральных чисел . Например, разложение по разрядам десятичной дроби 45,6072 таково: 45,6072=40+5+0,6+0,007+0,0002 . А свойства сложения от разложения десятичной дроби по разрядам позволяют перейти к другим представлениям этой десятичной дроби, например, 45,6072=45+0,6072 , или 45,6072=40,6+5,007+0,0002 , или 45,6072=45,0072+0,6 .

Конечные десятичные дроби

До этого момента мы говорили лишь о десятичных дробях, в записи которых после десятичной запятой находится конечное число цифр. Такие дроби называют конечными десятичными дробями.

Определение.

Конечные десятичные дроби – это десятичные дроби, в записях которых содержится конечное число знаков (цифр).

Приведем несколько примеров конечных десятичных дробей: 0,317 , 3,5 , 51,1020304958 , 230 032,45 .

Однако не всякая обыкновенная дробь может быть представлена в виде конечной десятичной дроби. К примеру, дробь 5/13 не может быть заменена равной ей дробью с одним из знаменателей 10, 100, … , следовательно, не может быть переведена в конечную десятичную дробь. Подробнее об этом мы поговорим в разделе теории перевод обыкновенных дробей в десятичные дроби .

Бесконечные десятичные дроби: периодические дроби и непериодические дроби

В записи десятичной дроби после запятой можно допустить возможность наличия бесконечного количества цифр. В этом случае мы придем к рассмотрению так называемых бесконечных десятичных дробей.

Определение.

Бесконечные десятичные дроби – это десятичные дроби, в записи которых находится бесконечное множество цифр.

Понятно, что бесконечные десятичные дроби мы не можем записать в полном виде, поэтому в их записи ограничиваются лишь некоторым конечным числом цифр после запятой и ставят многоточие, указывающее на бесконечно продолжающуюся последовательность цифр. Приведем несколько примеров бесконечных десятичных дробей: 0,143940932… , 3,1415935432… , 153,02003004005… , 2,111111111… , 69,74152152152… .

Если внимательно посмотреть на две последние бесконечные десятичные дроби, то в дроби 2,111111111… хорошо видна бесконечно повторяющаяся цифра 1 , а в дроби 69,74152152152… , начиная с третьего знака после запятой, отчетливо видна повторяющаяся группа цифр 1 , 5 и 2 . Такие бесконечные десятичные дроби называют периодическими.

Определение.

Периодические десятичные дроби (или просто периодические дроби ) – это бесконечные десятичные дроби, в записи которых, начиная с некоторого знака после запятой, бесконечно повторяется какая-нибудь цифра или группа цифр, которую называют периодом дроби .

Например, периодом периодической дроби 2,111111111… является цифра 1 , а периодом дроби 69,74152152152… является группа цифр вида 152 .

Для бесконечных периодических десятичных дробей принята особая форма записи. Для краткости условились период записывать один раз, заключая его в круглые скобки. Например, периодическая дробь 2,111111111… записывается как 2,(1) , а периодическая дробь 69,74152152152… записывается как 69,74(152) .

Стоит отметить, что для одной и той же периодической десятичной дроби можно указать различные периоды. Например, периодическую десятичную дробь 0,73333… можно рассматривать как дробь 0,7(3) с периодом 3 , а также как дробь 0,7(33) с периодом 33 , и так далее 0,7(333), 0,7(3333), … Также на периодическую дробь 0,73333… можно посмотреть и так: 0,733(3) , или так 0,73(333) и т.п. Здесь, чтобы избежать многозначности и разночтений, условимся рассматривать в качестве периода десятичной дроби самую короткую из всех возможных последовательностей повторяющихся цифр, и начинающуюся с самой близкой позиции к десятичной запятой. То есть, периодом десятичной дроби 0,73333… будем считать последовательность из одной цифры 3 , и периодичность начинается со второй позиции после запятой, то есть, 0,73333…=0,7(3) . Еще пример: периодическая дробь 4,7412121212… имеет период 12 , периодичность начинается с третьей цифры после запятой, то есть, 4,7412121212…=4,74(12) .

Бесконечные десятичные периодические дроби получаются при переводе в десятичные дроби обыкновенных дробей, знаменатели которых содержат простые множители, отличные от 2 и 5 .

Здесь же стоит сказать о периодических дробях с периодом 9 . Приведем примеры таких дробей: 6,43(9) , 27,(9) . Эти дроби являются другой записью периодических дробей с периодом 0 , и их принято заменять периодическими дробями с периодом 0 . Для этого период 9 заменяют периодом 0 , а значение следующего по старшинству разряда увеличивают на единицу. Например, дробь с периодом 9 вида 7,24(9) заменяется периодической дробью с периодом 0 вида 7,25(0) или равной ей конечной десятичной дробью 7,25 . Еще пример: 4,(9)=5,(0)=5 . Равенство дроби с периодом 9 и соответствующей ей дроби с периодом 0 легко устанавливается, после замены этих десятичных дробей равными им обыкновенными дробями.

Наконец, повнимательнее рассмотрим бесконечные десятичные дроби, в записи которых отсутствует бесконечно повторяющаяся последовательность цифр. Их называют непериодическими.

Определение.

Непериодические десятичные дроби (или просто непериодические дроби ) – это бесконечные десятичные дроби, не имеющие периода.

Иногда непериодические дроби имеют вид, схожий с видом периодических дробей, например, 8,02002000200002… - непериодическая дробь. В этих случаях следует быть особо внимательными, чтобы заметить разницу.

Отметим, что непериодические дроби не переводятся в обыкновенные дроби, бесконечные непериодические десятичные дроби представляют иррациональные числа .

Действия с десятичными дробями

Одним из действий с десятичными дробями является сравнение, также определены четыре основных арифметических действия с десятичными дробями : сложение, вычитание, умножение и деление. Рассмотрим отдельно каждое из действий с десятичными дробями.

Сравнение десятичных дробей по сути базируется на сравнении обыкновенных дробей , отвечающих сравниваемым десятичным дробям. Однако перевод десятичных дробей в обыкновенные является достаточно трудоемким действием, да и бесконечные непериодические дроби не могут быть представлены в виде обыкновенной дроби, поэтому удобно использовать поразрядное сравнение десятичных дробей. Поразрядное сравнение десятичных дробей аналогично сравнению натуральных чисел . Для получения более детальной информации рекомендуем изучить материал статьи сравнение десятичных дробей, правила, примеры, решения .

Переходим к следующему действию - умножению десятичных дробей . Умножение конечных десятичных дробей проводится аналогично вычитание десятичных дробей, правила, примеры, решения умножению столбиком натуральных чисел. В случае периодических дробей умножение можно свести к умножению обыкновенных дробей . В свою очередь умножение бесконечных непериодических десятичных дробей после их округления сводится к умножению конечных десятичных дробей. Рекомендуем к дальнейшему изучению материал статьи умножение десятичных дробей, правила, примеры, решения .

Десятичные дроби на координатном луче

Между точками и десятичными дробями существует взаимно однозначное соответствие.

Разберемся, как строятся точки на координатном луче, соответствующие данной десятичной дроби.

Конечные десятичные дроби и бесконечные периодические десятичные дроби мы можем заменить равными им обыкновенными дробями, после чего построить соответствующие обыкновенные дроби на координатном луче . Например, десятичной дроби 1,4 отвечает обыкновенная дробь 14/10 , поэтому точка с координатой 1,4 удалена от начала отсчета в положительном направлении на 14 отрезков, равных десятой доле единичного отрезка.

Десятичные дроби можно отмечать на координатном луче, отталкиваясь от разложения данной десятичной дроби по разрядам. Например, пусть нам нужно построить точку с координатой 16,3007 , так как 16,3007=16+0,3+0,0007 , то в данную точку можно попасть, последовательно откладывая от начала координат 16 единичных отрезков, 3 отрезка, длина которых равна десятой доле единичного, и 7 отрезков, длина которого равна десятитысячной доле единичного отрезка.

Такой способ построения десятичных чисел на координатном луче позволяет сколь угодно близко приблизиться к точке, отвечающей бесконечной десятичной дроби.

Иногда возможно точно построить точку, соответствующую бесконечной десятичной дроби. Например, , тогда этой бесконечной десятичной дроби 1,41421… соответствует точка координатного луча, удаленная от начала координат на длину диагонали квадрата со стороной 1 единичный отрезок.

Обратный процесс получения десятичной дроби, соответствующей данной точке на координатном луче, представляет собой так называемое десятичное измерение отрезка . Разберемся, как оно проводится.

Пусть наша задача заключается в том, чтобы попасть из начала отсчета в данную точку координатной прямой (или бесконечно приблизиться к ней, если попасть в нее не получается). При десятичном измерении отрезка мы можем последовательно откладывать от начала отсчета любое количество единичных отрезков, далее отрезков, длина которых равна десятой доле единичного, затем отрезков, длина которых равна сотой доле единичного, и т.д. Записывая количество отложенных отрезков каждой длины, мы получим десятичную дробь, соответствующую данной точке на координатном луче.

К примеру, чтобы попасть в точку М на приведенном выше рисунке, нужно отложить 1 единичный отрезок и 4 отрезка, длина которых равна десятой доле единичного. Таким образом, точке М соответствует десятичная дробь 1,4 .

Понятно, что точкам координатного луча, в которые невозможно попасть в процессе десятичного измерения, соответствуют бесконечные десятичные дроби.

Список литературы.

Математика : учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. - 21-е изд., стер. - М.: Мнемозина, 2007. - 280 с.: ил. ISBN 5-346-00699-0.
Математика. 6 класс: учеб. для общеобразоват. учреждений / [Н. Я. Виленкин и др.]. - 22-е изд., испр. - М.: Мнемозина, 2008. - 288 с.: ил. ISBN 978-5-346-00897-2.
Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Предыдущая статья: Чему равна скорость света Следующая статья: Гармонические колебания Физика формула частоты колебаний