Seksioni i një trekëndëshi duke përdorur teoremën e Pitagorës. Probleme duke përdorur teoremën e Pitagorës

Çdo nxënës shkolle e di se hipotenuza është gjithmonë katrori e barabartë me shumën këmbët, secila prej të cilave është në katror. Ky pohim quhet teorema e Pitagorës. Ajo është një nga më teorema të famshme trigonometria dhe matematika në përgjithësi. Le t'i hedhim një vështrim më të afërt.

Koncepti i një trekëndëshi kënddrejtë

Përpara se të shqyrtojmë teoremën e Pitagorës, në të cilën katrori i hipotenuzës është i barabartë me shumën e këmbëve që janë në katror, ​​duhet të shqyrtojmë konceptin dhe vetitë. trekëndësh kënddrejtë, për të cilën është e vlefshme teorema.

trekëndësh - figurë e sheshtë që ka tre kënde dhe tre brinjë. Një trekëndësh kënddrejtë, siç sugjeron emri i tij, ka një kënd të drejtë, domethënë ky kënd është i barabartë me 90 o.

Nga vetitë e përgjithshme për të gjithë trekëndëshat, dihet se shuma e të tre këndeve të kësaj figure është 180 o, që do të thotë se për një trekëndësh kënddrejtë, shuma e dy këndeve që nuk janë kënde të drejta është 180 o - 90 o = 90 o. Ky fakt i fundit do të thotë se çdo kënd në një trekëndësh kënddrejtë që nuk është i drejtë do të jetë gjithmonë më i vogël se 90 o.

Pala që qëndron kundër kënd i drejtë, zakonisht quhet hipotenuzë. Dy anët e tjera janë këmbët e trekëndëshit, ato mund të jenë të barabarta me njëra-tjetrën ose mund të jenë të ndryshme. Nga trigonometria dimë se sa më i madh të jetë këndi kundër të cilit shtrihet një brinjë e një trekëndëshi, aq më e madhe është gjatësia e asaj brinjë. Kjo do të thotë se në një trekëndësh kënddrejtë hipotenuza (shtrihet përballë këndit 90 o) do të jetë gjithmonë më e madhe se çdo këmbë (shtrihet përballë këndeve< 90 o).

Shënimi matematik i teoremës së Pitagorës

Kjo teoremë thotë se katrori i hipotenuzës është i barabartë me shumën e këmbëve, secila prej të cilave është në katror më parë. Për ta shkruar këtë formulim matematikisht, merrni parasysh një trekëndësh kënddrejtë në të cilin brinjët a, b dhe c janë përkatësisht dy këmbët dhe hipotenuza. Në këtë rast, teorema, e cila formulohet si katrori i hipotenuzës është i barabartë me shumën e katrorëve të këmbëve, mund të përfaqësohet me formulën e mëposhtme: c 2 = a 2 + b 2. Prej këtu mund të merren formula të tjera të rëndësishme për praktikë: a = √(c 2 - b 2), b = √(c 2 - a 2) dhe c = √(a 2 + b 2).

Vini re se në rastin e një drejtkëndëshi trekëndësh barabrinjës, domethënë a = b, formulimi: katrori i hipotenuzës është i barabartë me shumën e këmbëve, secila prej të cilave është në katror, ​​shkruhet matematikisht si më poshtë: c 2 = a 2 + b 2 = 2a 2, që nënkupton barazi: c = a√2.

Sfondi historik

Teorema e Pitagorës, e cila thotë se katrori i hipotenuzës është i barabartë me shumën e këmbëve, secila prej të cilave është në katror, ​​ishte e njohur shumë përpara se filozofi i famshëm grek t'i kushtonte vëmendje. Shumë papirus Egjipti i lashtë, si dhe pllaka balte të babilonasve konfirmojnë se këta popuj përdorën vetinë e shënuar të brinjëve të një trekëndëshi kënddrejtë. Për shembull, një nga piramidat e para egjiptiane, Piramida e Khafre, ndërtimi i së cilës daton në shekullin e 26 para Krishtit (2000 vjet para jetës së Pitagorës), u ndërtua bazuar në njohuritë e raportit të pamjes në një trekëndësh kënddrejtë 3x4x5. .

Pse atëherë teorema tani mban emrin e greqishtes? Përgjigja është e thjeshtë: Pitagora është i pari që vërtetoi matematikisht këtë teoremë. Në babilonas dhe egjiptian të mbijetuar burime të shkruara Ai flet vetëm për përdorimin e tij, por nuk jep asnjë provë matematikore.

Besohet se Pitagora e vërtetoi teoremën në fjalë duke përdorur vetitë trekëndësha të ngjashëm, të cilën e ka marrë duke vizatuar lartësinë në një trekëndësh kënddrejtë nga një kënd 90 o në hipotenuzë.

Një shembull i përdorimit të teoremës së Pitagorës

Le të shqyrtojmë detyrë e thjeshtë: është e nevojshme të përcaktohet gjatësia e shkallës së pjerrët L, nëse dihet se ajo ka një lartësi H = 3 metra, dhe distanca nga muri kundrejt të cilit mbështetet shkalla deri në këmbën e saj është P = 2,5 metra.

Në këtë rast, H dhe P janë këmbët, dhe L është hipotenuza. Meqenëse gjatësia e hipotenuzës është e barabartë me shumën e katrorëve të këmbëve, marrim: L 2 = H 2 + P 2, nga ku L = √(H 2 + P 2) = √(3 2 + 2,5 2 ) = 3.905 metra ose 3 m dhe 90, 5 cm.

Sigurohuni që trekëndëshi që ju jepet të jetë një trekëndësh kënddrejtë, pasi teorema e Pitagorës zbatohet vetëm për trekëndëshat kënddrejtë.

• Në trekëndëshat kënddrejtë, njëri nga tre këndet është gjithmonë 90 gradë.

Një kënd i drejtë në një trekëndësh kënddrejtë tregohet nga një simbol katror, ​​në vend të simbolit të kurbës që përfaqëson këndet e zhdrejtë. Etiketoni anët e trekëndëshit. Etiketoni këmbët si "a" dhe "b" (këmbët janë anët që kryqëzohen në kënde të drejta), dhe hipotenuza si "c" (hipotenuza është më e anën e madhe

trekëndëshi kënddrejtë, i shtrirë përballë këndit të drejtë). Teorema e Pitagorës ju lejon të gjeni çdo anë të një trekëndëshi kënddrejtë (nëse njihen dy brinjët e tjera). Përcaktoni cilën anë (a, b, c) duhet të gjeni.

• Për shembull, jepet një hipotenuzë e barabartë me 5, dhe jepet një këmbë e barabartë me 3. Në këtë rast, është e nevojshme të gjendet këmba e dytë. Ne do t'i kthehemi këtij shembulli më vonë.
• Nëse dy anët e tjera janë të panjohura, ju duhet të gjeni gjatësinë e njërës prej anëve të panjohura për të zbatuar teoremën e Pitagorës. Për ta bërë këtë, përdorni bazën funksionet trigonometrike(nëse ju jepet vlera e njërit prej këndeve të zhdrejtë).

Zëvendësoni vlerat që ju janë dhënë (ose vlerat që keni gjetur) në formulën a 2 + b 2 = c 2. Mos harroni se a dhe b janë këmbë, dhe c është hipotenuza.

• Në shembullin tonë, shkruani: 3² + b² = 5².

Sheshoni secilën anë të njohur. Ose lini fuqitë - mund t'i vendosni numrat në katror më vonë.

• Në shembullin tonë, shkruani: 9 + b² = 25.

Të ndara anën e panjohur në njërën anë të ekuacionit. Për ta bërë këtë, transferoni vlerat e njohura në anën tjetër të ekuacionit. Nëse gjeni hipotenuzën, atëherë në teoremën e Pitagorës ajo tashmë është e izoluar në njërën anë të ekuacionit (kështu që nuk keni nevojë të bëni asgjë).

• Në shembullin tonë, zhvendoseni 9 në anën e djathtë të ekuacionit për të izoluar të panjohurën b². Do të merrni b² = 16.

Hiq rrënjë katrore nga të dyja anët e ekuacionit pasi njëra anë e ekuacionit ka të panjohurën (në katror) dhe ana tjetër ka anëtar i lirë(numri).

• Në shembullin tonë, b² = 16. Merrni rrënjën katrore të të dy anëve të ekuacionit dhe merrni b = 4. Kështu, pjesa e dytë është 4.

Përdorni teoremën e Pitagorës në jetën e përditshme, pasi mund të përdoret në numër i madh situata praktike.

• Për ta bërë këtë, mësoni të njihni trekëndëshat kënddrejtë në jetën e përditshme - në çdo situatë në të cilën dy objekte (ose vija) kryqëzohen në kënde të drejta, dhe një objekt i tretë (ose vijë) lidh (diagonalisht) majat e dy objekteve të parë (ose linjat), mund të përdorni teoremën e Pitagorës për të gjetur anën e panjohur (nëse dy anët e tjera janë të njohura). Shembull: jepet një shkallë e mbështetur në një ndërtesë. Pjesa e poshtme e shkallëve është 5 metra nga baza e murit. Pjesa e sipërme
  • “5 metra nga baza e murit” do të thotë se a = 5; "Ndodhet 20 metra nga toka" do të thotë se b = 20 (d.m.th., ju jepen dy këmbët e një trekëndëshi kënddrejtë, pasi muri i ndërtesës dhe sipërfaqja e Tokës kryqëzohen në kënde të drejta). Gjatësia e shkallës është gjatësia e hipotenuzës, e cila nuk dihet.
    • a² + b² = c²
    • (5)² + (20)² = c²
    • 25 + 400 = c²
    • 425 = c²
    • c = √425
    • c = 20.6. Kështu, gjatësia e përafërt e shkallëve është 20.6 metra.

Potenciali për kreativitet zakonisht i atribuohet shkencave humane, duke ia lënë shkencën natyrore analizës, qasjes praktike dhe gjuhës së thatë të formulave dhe numrave. Matematika për të lëndët humanitare Ju nuk mund të lidheni me të në asnjë mënyrë. Por pa kreativitet nuk do të shkoni larg në "mbretëreshën e të gjitha shkencave" - ​​njerëzit e kanë ditur këtë për një kohë të gjatë. Që nga koha e Pitagorës, për shembull.

Tekstet shkollore, për fat të keq, zakonisht nuk shpjegojnë se në matematikë është e rëndësishme jo vetëm të grumbullohen teorema, aksioma dhe formula. Është e rëndësishme ta kuptoni dhe ta ndjeni atë parimet themelore. Dhe në të njëjtën kohë, përpiquni të çlironi mendjen tuaj nga klishe dhe të vërteta elementare - vetëm në kushte të tilla lindin të gjitha zbulimet e mëdha.

Zbulime të tilla përfshijnë atë që ne e njohim sot si teorema e Pitagorës. Me ndihmën e saj, ne do të përpiqemi të tregojmë se matematika jo vetëm që mundet, por duhet të jetë emocionuese. Dhe se kjo aventurë është e përshtatshme jo vetëm për budallenj me syze të trasha, por për të gjithë ata që janë të fortë në mendje dhe të fortë në shpirt.

Nga historia e çështjes

Në mënyrë të rreptë, megjithëse teorema quhet "teorema e Pitagorës", vetë Pitagora nuk e zbuloi atë. Trekëndëshi kënddrejtë dhe vetitë e tij të veçanta janë studiuar shumë përpara tij. Ekzistojnë dy këndvështrime polare për këtë çështje. Sipas një versioni, Pitagora ishte i pari që gjeti një provë të plotë të teoremës. Sipas një tjetri, prova nuk i përket autorësisë së Pitagorës.

Sot nuk mund të kontrolloni më kush ka të drejtë dhe kush ka gabuar. Ajo që dihet është se prova e Pitagorës, nëse ka ekzistuar ndonjëherë, nuk ka mbijetuar. Sidoqoftë, ka sugjerime se prova e famshme nga Elementet e Euklidit mund t'i përkasë Pitagorës dhe Euklidi vetëm e regjistroi atë.

Dihet gjithashtu sot se problemet rreth një trekëndëshi kënddrejtë gjenden në burimet egjiptiane nga koha e faraonit Amenemhat I, në gjuhën babilonase. tableta balte periudha e mbretërimit të mbretit Hamurabi, në traktatin e lashtë indian "Sulva Sutra" dhe veprën e lashtë kineze "Zhou-bi suan jin".

Siç mund ta shihni, teorema e Pitagorës ka pushtuar mendjet e matematikanëve që nga kohërat e lashta. Këtë e vërtetojnë rreth 367 prova të ndryshme që ekzistojnë sot. Në këtë, asnjë teoremë tjetër nuk mund të konkurrojë me të. Ndër autorët e famshëm të provave mund të kujtojmë Leonardo da Vincin dhe presidentin e njëzetë të SHBA-së James Garfield. E gjithë kjo flet për rëndësinë ekstreme të kësaj teoreme për matematikën: shumica e teoremave të gjeometrisë rrjedhin prej saj ose janë disi të lidhura me të.

Vërtetime të teoremës së Pitagorës

NË tekstet shkollore Ata kryesisht japin prova algjebrike. Por thelbi i teoremës është në gjeometri, kështu që le të shqyrtojmë së pari ato prova të teoremës së famshme që bazohen në këtë shkencë.

Dëshmia 1

Për më së shumti provë e thjeshtë Sipas teoremës së Pitagorës, për një trekëndësh kënddrejtë, duhet të vendosni kushte ideale: le të jetë trekëndëshi jo vetëm kënddrejtë, por edhe dykëndësh. Ka arsye për të besuar se ishte pikërisht ky lloj trekëndëshi që matematikanët e lashtë konsideruan fillimisht.

deklaratë "Një katror i ndërtuar mbi hipotenuzën e një trekëndëshi kënddrejtë është i barabartë me shumën e katrorëve të ndërtuar në këmbët e tij" mund të ilustrohet me vizatimin e mëposhtëm:

Shikoni trekëndëshin kënddrejtë dykëndësh ABC: Në hipotenuzën AC, mund të ndërtoni një katror të përbërë nga katër trekëndësha të barabartë me ABC-në origjinale. Dhe në brinjët AB dhe BC është ndërtuar një katror, ​​secili prej të cilëve përmban dy trekëndësha të ngjashëm.

Nga rruga, ky vizatim formoi bazën e shakave dhe karikaturave të shumta kushtuar teoremës së Pitagorës. Më i famshmi është ndoshta « Pantallona pitagoriane të barabartë në të gjitha drejtimet":

Dëshmia 2

Kjo metodë kombinon algjebrën dhe gjeometrinë dhe mund të konsiderohet si një variant i provës së lashtë indiane të matematikanit Bhaskari.

Ndërtoni një trekëndësh kënddrejtë me brinjë a, b dhe c(Fig. 1). Pastaj ndërtoni dy katrorë me brinjë të barabartë me shumën e gjatësive të dy këmbëve - (a+b). Në secilin nga katrorët, bëni ndërtime si në figurat 2 dhe 3.

Në katrorin e parë, ndërtoni katër trekëndësha të ngjashëm me ata në figurën 1. Rezultati është dy katrorë: njëri me brinjën a, i dyti me brinjën b.

Në sheshin e dytë, katër trekëndësha të ngjashëm të ndërtuar formojnë një katror me një brinjë e barabartë me hipotenuzën c.

Shuma e sipërfaqeve të katrorëve të ndërtuar në figurën 2 është e barabartë me sipërfaqen e katrorit që kemi ndërtuar me anën c në figurën 3. Kjo mund të kontrollohet lehtësisht duke llogaritur sipërfaqen e katrorëve në Fig. 2 sipas formulës. Dhe sipërfaqja e katrorit të gdhendur në figurën 3. duke zbritur sipërfaqet e katër trekëndëshave të barabartë kënddrejtë të gdhendur në katror nga sipërfaqja e një katrori të madh me një anë (a+b).

Duke shkruar të gjitha këto, ne kemi: a 2 +b 2 =(a+b) 2 – 2ab. Hapni kllapat, kryeni të gjitha llogaritjet e nevojshme algjebrike dhe merrni atë a 2 +b 2 = a 2 +b 2. Në këtë rast, zona e gdhendur në Fig. 3. katrori mund të llogaritet edhe duke përdorur formulën tradicionale S=c 2. ato. a 2 +b 2 =c 2– ju keni vërtetuar teoremën e Pitagorës.

Dëshmia 3

Vetë prova e lashtë indiane u përshkrua në shekullin e 12-të në traktatin "Kurora e dijes" ("Siddhanta Shiromani") dhe si argument kryesor autori përdor një apel drejtuar talenteve matematikore dhe aftësive vëzhguese të studentëve dhe ndjekësve: " Shikoni!”

Por ne do ta analizojmë këtë provë më në detaje:

Brenda katrorit, ndërtoni katër trekëndësha kënddrejtë siç tregohet në vizatim. Le të shënojmë anën e katrorit të madh, i njohur gjithashtu si hipotenuzë, Me. Le t'i quajmë këmbët e trekëndëshit A Dhe b. Sipas vizatimit, ana e katrorit të brendshëm është (a-b).

Përdorni formulën për sipërfaqen e një katrori S=c 2 për të llogaritur sipërfaqen e katrorit të jashtëm. Dhe në të njëjtën kohë llogarisni të njëjtën vlerë duke shtuar sipërfaqen e katrorit të brendshëm dhe sipërfaqet e të katër trekëndëshave kënddrejtë: (a-b) 2 2+4*1\2*a*b.

Ju mund të përdorni të dy opsionet për llogaritjen e sipërfaqes së një katrori për t'u siguruar që ato japin të njëjtin rezultat. Dhe kjo ju jep të drejtën ta shkruani atë c 2 =(a-b) 2 +4*1\2*a*b. Si rezultat i zgjidhjes, do të merrni formulën e teoremës së Pitagorës c 2 =a 2 +b 2. Teorema është vërtetuar.

Prova 4

Kjo provë kurioze e lashtë kineze u quajt "Karrika e nuses" - për shkak të figurës si karrige që rezulton nga të gjitha ndërtimet:

Ai përdor vizatimin që kemi parë tashmë në Fig. 3 në provën e dytë. Dhe katrori i brendshëm me anën c është ndërtuar në të njëjtën mënyrë si në provën e lashtë indiane të dhënë më sipër.

Nëse i preni mendërisht dy trekëndësha drejtkëndëshe jeshile nga vizatimi në Fig. 1, i zhvendosni në anët e kundërta të katrorit me anën c dhe i lidhni hipotenuset në hipotenusat e trekëndëshave jargavan, do të merrni një figurë të quajtur "karrige e nuses". (Fig. 2). Për qartësi, mund të bëni të njëjtën gjë me katrorë dhe trekëndësha letre. Do të siguroheni që "karrigia e nuses" të formohet nga dy katrorë: të vegjël me anë. b dhe i madh me një anë a.

Këto ndërtime i lejuan matematikanët e lashtë kinezë dhe ne, duke ndjekur ata, të arrinim në përfundimin se c 2 =a 2 +b 2.

Dëshmia 5

Kjo është një mënyrë tjetër për të gjetur një zgjidhje për teoremën e Pitagorës duke përdorur gjeometrinë. Quhet Metoda Garfield.

Ndërtoni një trekëndësh kënddrejtë ABC. Ne duhet ta vërtetojmë këtë BC 2 = AC 2 + AB 2.

Për ta bërë këtë, vazhdoni këmbën AC dhe ndërtoni një segment CD, e cila është e barabartë me këmbën AB. Ulni pingulen pas Krishtit segment ED. Segmentet ED Dhe AC janë të barabartë. Lidhni pikat E Dhe NË, dhe gjithashtu E Dhe ME dhe merrni një vizatim si në foton më poshtë:

Për të vërtetuar kullën, ne përsëri i drejtohemi metodës që kemi provuar tashmë: gjejmë zonën e figurës që rezulton në dy mënyra dhe barazojmë shprehjet me njëra-tjetrën.

Gjeni sipërfaqen e një shumëkëndëshi ABED mund të bëhet duke mbledhur sipërfaqet e tre trekëndëshave që e formojnë atë. Dhe një prej tyre, ERU, nuk është vetëm drejtkëndëshe, por edhe dykëndëshe. Le të mos e harrojmë gjithashtu AB=CD, AC=ED Dhe BC=SE– kjo do të na lejojë të thjeshtojmë regjistrimin dhe të mos e mbingarkojmë atë. Pra, S ABED =2*1/2(AB*AC)+1/2ВС 2.

Në të njëjtën kohë, është e qartë se ABED- Ky është një trapez. Prandaj, ne llogarisim zonën e saj duke përdorur formulën: S ABED =(DE+AB)*1/2AD. Për llogaritjet tona, është më e përshtatshme dhe më e qartë të përfaqësohet segmenti pas Krishtit si shuma e segmenteve AC Dhe CD.

Le të shkruajmë të dyja mënyrat për të llogaritur sipërfaqen e një figure, duke vendosur një shenjë të barabartë midis tyre: AB*AC+1/2BC 2 =(DE+AB)*1/2(AC+CD). Ne përdorim barazinë e segmenteve tashmë të njohura për ne dhe të përshkruara më lart për të thjeshtuar anën e djathtë hyrjet: AB*AC+1/2BC 2 =1/2(AB+AC) 2. Tani le të hapim kllapat dhe të transformojmë barazinë: AB*AC+1/2BC 2 =1/2AC 2 +2*1/2(AB*AC)+1/2AB 2. Pasi të kemi përfunduar të gjitha transformimet, marrim pikërisht atë që na nevojitet: BC 2 = AC 2 + AB 2. Ne kemi vërtetuar teoremën.

Sigurisht, kjo listë e provave është larg të qenit e plotë. Teorema e Pitagorës mund të vërtetohet edhe duke përdorur vektorë, numra kompleksë, ekuacione diferenciale, stereometri, etj. Dhe madje edhe fizikanët: nëse, për shembull, lëngu derdhet në vëllime katrore dhe trekëndore të ngjashme me ato të treguara në vizatime. Duke derdhur lëng, mund të vërtetoni barazinë e zonave dhe si rezultat vetë teoremën.

Disa fjalë për trenjakët e Pitagorës

Kjo çështje studiohet pak ose aspak në kurrikulën shkollore. Ndërkohë, ai është shumë interesant dhe ka vlerë të madhe në gjeometri. Treshe të Pitagorës përdoren për të zgjidhur shumë problemet matematikore. Kuptimi i tyre mund të jetë i dobishëm për ju në edukimin e mëtejshëm.

Pra, çfarë janë trenjakët e Pitagorës? Kështu e quajnë numrat natyrorë, të mbledhura në treshe, shuma e katrorëve të dy prej të cilëve është e barabartë me numrin e tretë në katror.

Treshe të Pitagorës mund të jenë:

• primitiv (të tre numrat janë relativisht të thjeshtë);
• jo primitiv (nëse çdo numër i një treshe shumëzohet me të njëjtin numër, ju merrni një trefish të ri, i cili nuk është primitiv).

Edhe para epokës sonë, egjiptianët e lashtë ishin të magjepsur nga mania për numrin e treshave të Pitagorës: në problematikë ata konsideronin një trekëndësh kënddrejtë me brinjë 3, 4 dhe 5 njësi. Nga rruga, çdo trekëndësh, anët e të cilit janë të barabarta me numrat nga trefishi i Pitagorës është drejtkëndor si parazgjedhje.

Shembuj të treshave të Pitagorës: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20 ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34) , (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), ( 14, 48, 50), (30, 40, 50), etj.

Zbatimi praktik i teoremës

Teorema e Pitagorës përdoret jo vetëm në matematikë, por edhe në arkitekturë dhe ndërtim, astronomi dhe madje edhe letërsi.

Së pari për ndërtimin: teorema e Pitagorës gjen në të aplikim të gjerë në detyra nivele të ndryshme kompleksiteti. Për shembull, shikoni një dritare romane:

Le të shënojmë gjerësinë e dritares si b, atëherë rrezja e gjysmërrethit të madh mund të shënohet si R dhe shprehin përmes b: R=b/2. Rrezja e gjysmërretheve më të vogla mund të shprehet edhe përmes b: r=b/4. Në këtë problem na intereson rrezja e rrethit të brendshëm të dritares (le ta quajmë atë fq).

Teorema e Pitagorës është thjesht e dobishme për t'u llogaritur r. Për ta bërë këtë, ne përdorim një trekëndësh kënddrejtë, i cili tregohet nga një vijë me pika në figurë. Hipotenuza e një trekëndëshi përbëhet nga dy rreze: b/4+p. Njëra këmbë përfaqëson rrezen b/4, një tjetër b/2-p. Duke përdorur teoremën e Pitagorës, ne shkruajmë: (b/4+p) 2 =(b/4) 2 +(b/2-p) 2. Më pas, hapim kllapat dhe marrim b 2 /16+ bp/2+p 2 =b 2 /16+b 2 /4-bp+p 2. Le ta shndërrojmë këtë shprehje në bp/2=b 2 /4-bp. Dhe pastaj ne i ndajmë të gjitha termat me b, ne paraqesim të ngjashme për të marrë 3/2*p=b/4. Dhe në fund e gjejmë atë p=b/6- e cila është ajo që na duhej.

Duke përdorur teoremën, mund të llogarisni gjatësinë e mahijeve për një çati gable. Përcaktoni se sa e lartë nevojitet një kullë telefoni celular që sinjali të arrijë një të caktuar zgjidhje. Dhe madje instaloni një pemë të Krishtlindjes në mënyrë të qëndrueshme në sheshin e qytetit. Siç mund ta shihni, kjo teoremë jeton jo vetëm në faqet e teksteve shkollore, por shpesh është e dobishme në jetën reale.

Në letërsi, teorema e Pitagorës ka frymëzuar shkrimtarët që nga lashtësia dhe vazhdon të jetë kështu edhe në kohën tonë. Për shembull, shkrimtari gjerman i shekullit të nëntëmbëdhjetë Adelbert von Chamisso u frymëzua të shkruante një sonet:

Drita e së vërtetës nuk do të shuhet shpejt,
Por, pasi shkëlqeu, nuk ka gjasa të shpërndahet
Dhe, si mijëra vjet më parë,
Nuk do të shkaktojë dyshime apo polemika.

Më e mençura kur të prek shikimin
Drita e së vërtetës, falënderoj perënditë;
Dhe njëqind dema, të therur, gënjejnë -
Një dhuratë kthimi nga Pitagora me fat.

Që atëherë demat kanë ulëritur në mënyrë të dëshpëruar:
Përgjithmonë alarmoi fisin e demave
Ngjarja e përmendur këtu.

Atyre u duket: koha po vjen,
Dhe ata do të sakrifikohen përsëri
Një teoremë e madhe.

(përkthimi nga Viktor Toporov)

Dhe në shekullin e njëzetë shkrimtar sovjetik Evgeniy Veltistov në librin e tij "Aventurat e Elektronikës" i kushtoi një kapitull të tërë provave të teoremës së Pitagorës. Dhe një gjysmë kapitulli tjetër për një histori për një botë dydimensionale që mund të ekzistonte nëse teorema e Pitagorës do të bëhej një ligj themelor dhe madje një fe për një botë të vetme. Të jetosh atje do të ishte shumë më e lehtë, por edhe shumë më e mërzitshme: për shembull, askush nuk e kupton atje kuptimin e fjalëve "të rrumbullakët" dhe "me gëzof".

Dhe në librin "Aventurat e Elektronikës", autori, me gojën e mësuesit të matematikës Taratar, thotë: "Gjëja kryesore në matematikë është lëvizja e mendimit, idetë e reja". Është pikërisht ky fluturim krijues i mendimit që krijon teoremën e Pitagorës - jo më kot ajo ka kaq shumë prova të ndryshme. Kjo ju ndihmon të shkoni përtej kufijve të të njohurës dhe t'i shikoni gjërat e njohura në një mënyrë të re.

konkluzioni

Ky artikull është krijuar për t'ju ndihmuar të shikoni përtej kurrikula shkollore në matematikë dhe mësoni jo vetëm ato prova të teoremës së Pitagorës që jepen në tekstet "Gjeometria 7-9" (L.S. Atanasyan, V.N. Rudenko) dhe "Gjeometria 7-11" (A.V. Pogorelov), por dhe mënyra të tjera interesante për të vërtetuar teorema e famshme. Dhe gjithashtu shihni shembuj se si mund të zbatohet teorema e Pitagorës në jetën e përditshme.

Së pari, ky informacion do t'ju lejojë të kualifikoheni për më shumë rezultate të larta në mësimet e matematikës - informacione për lëndën nga burime shtesë vlerësohen gjithmonë shumë.

Së dyti, ne donim t'ju ndihmonim të kuptoni se si matematika shkencë interesante. Sigurohuni shembuj specifikë se në të ka gjithmonë vend për kreativitet. Shpresojmë që Teorema e Pitagorës dhe ky artikull do t'ju frymëzojnë kërkime të pavarura dhe zbulime emocionuese në matematikë dhe shkenca të tjera.

Na tregoni në komente nëse ju gjetën interesante provat e paraqitura në artikull. A ju duk i dobishëm ky informacion në studimet tuaja? Na shkruani se çfarë mendoni për teoremën e Pitagorës dhe këtë artikull - ne do të jemi të lumtur t'i diskutojmë të gjitha këto me ju.

blog.site, kur kopjoni materialin plotësisht ose pjesërisht, kërkohet një lidhje me burimin origjinal.

(sipas papirusit 6619 të Muzeut të Berlinit). Sipas Cantor, harpedonaptet, ose "tërheqësit e litarit", ndërtonin kënde të drejta duke përdorur trekëndësha kënddrejtë me brinjë 3, 4 dhe 5.

Është shumë e lehtë të riprodhosh metodën e tyre të ndërtimit. Le të marrim një litar 12 m të gjatë dhe t'i lidhim një rrip me ngjyrë në një distancë prej 3 m nga njëri skaj dhe 4 metra nga tjetri. Këndi i duhur do të jetë ndërmjet anëve 3 dhe 4 metra të gjatë. Harpedonaptëve mund t'u kundërshtohet se metoda e tyre e ndërtimit bëhet e tepërt nëse përdoret, për shembull, një shesh druri, i cili përdoret nga të gjithë marangozët. Në të vërtetë, janë të njohura vizatimet egjiptiane në të cilat gjendet një mjet i tillë, për shembull, vizatime që përshkruajnë një punëtori zdrukthtari.

Dihet disi më shumë për teoremën e Pitagorës tek babilonasit. Në një tekst që daton në kohën e Hamurabit, pra në vitin 2000 p.e.s. e. , jepet një llogaritje e përafërt e hipotenuzës së një trekëndëshi kënddrejtë. Nga kjo mund të konkludojmë se në Mesopotami ata ishin në gjendje të kryenin llogaritjet me trekëndësha kënddrejtë, të paktën në disa raste. Bazuar, nga njëra anë, në nivelin aktual të njohurive për matematikën egjiptiane dhe babilonase, dhe nga ana tjetër, në një studim kritik Burimet greke, Van der Waerden (një matematikan holandez) arriti në përfundimin se ka shumë të ngjarë që teorema mbi katrorin e hipotenuzës ishte e njohur në Indi tashmë rreth shekullit të 18-të para Krishtit. e.

Rreth vitit 400 para Krishtit. e., sipas Proclus, Platoni dha një metodë për gjetjen Treshe pitagoriane, duke kombinuar algjebrën dhe gjeometrinë. Rreth vitit 300 para Krishtit. e. Prova më e vjetër aksiomatike e teoremës së Pitagorës u shfaq në Elementet e Euklidit.

Formulimet

Formulimi gjeometrik:

Teorema fillimisht u formulua si më poshtë:

Formulimi algjebrik:

Kjo është, duke treguar gjatësinë e hipotenuzës së trekëndëshit me , dhe gjatësinë e këmbëve me dhe :

Të dy formulimet e teoremës janë ekuivalente, por formulimi i dytë është më elementar dhe nuk kërkon konceptin e zonës. Kjo do të thotë, pohimi i dytë mund të verifikohet pa ditur asgjë për sipërfaqen dhe duke matur vetëm gjatësitë e brinjëve të një trekëndëshi kënddrejtë.

Teorema e Pitagorës së kundërt:

Dëshmi

Aktiv për momentin 367 prova të kësaj teoreme janë regjistruar në literaturën shkencore. Ndoshta, teorema e Pitagorës është e vetmja teoremë me një numër kaq mbresëlënës provash. Ky diversitet mund të shpjegohet vetëm rëndësi themelore teorema për gjeometrinë.

Sigurisht, konceptualisht të gjitha ato mund të ndahen në një numër të vogël klasash. Më të famshmit prej tyre: provat me metodën e zonës, provat aksiomatike dhe ekzotike (për shembull, duke përdorur ekuacionet diferenciale).

Përmes trekëndëshave të ngjashëm

Vërtetimi i mëposhtëm i formulimit algjebrik është vërtetimi më i thjeshtë, i ndërtuar drejtpërdrejt nga aksiomat. Në veçanti, ai nuk përdor konceptin e zonës së një figure.

Le ABC ka një trekëndësh kënddrejtë me kënd të drejtë C. Le të nxjerrim lartësinë nga C dhe shënoni bazën e tij me H. Trekëndëshi ACH të ngjashme me një trekëndësh ABC në dy qoshe. Po kështu, trekëndësh CBH të ngjashme ABC. Duke futur shënimin

marrim

Çfarë është ekuivalente

Duke e shtuar atë, marrim

, që është ajo që duhej vërtetuar

Provat duke përdorur metodën e zonës

Provat e mëposhtme, megjithë thjeshtësinë e tyre të dukshme, nuk janë aspak aq të thjeshta. Ata të gjithë përdorin vetitë e zonës, vërtetimi i së cilës është më kompleks se vërtetimi i vetë teoremës së Pitagorës.

Vërtetimi nëpërmjet ekuiplotësimit

1. Le të rregullojmë katër trekëndësha kënddrejtë të barabartë siç tregohet në figurën 1.
2. Katërkëndësh me brinjë cështë një katror, ​​pasi shuma e dy qoshe të mprehta 90°, dhe këndi i shpalosur është 180°.
3. Sipërfaqja e të gjithë figurës është e barabartë, nga njëra anë, me sipërfaqen e një katrori me anë (a + b), dhe nga ana tjetër, me shumën katër katrorë trekëndëshat dhe sipërfaqja e katrorit të brendshëm.

Q.E.D.

Prova e Euklidit

Ideja e vërtetimit të Euklidit është si vijon: le të përpiqemi të vërtetojmë se gjysma e sipërfaqes së katrorit të ndërtuar mbi hipotenuzë është e barabartë me shumën e gjysmës së sipërfaqeve të katrorëve të ndërtuar në këmbë, dhe më pas sipërfaqet e katrorët e mëdhenj dhe dy të vegjël janë të barabartë.

Le të shohim vizatimin në të majtë. Mbi të ndërtuam katrorë në brinjët e një trekëndëshi kënddrejtë dhe vizatuam një rreze s nga kulmi i këndit të drejtë C pingul me hipotenuzën AB, katrorin ABIK, të ndërtuar mbi hipotenuzë, e pret në dy drejtkëndësha - BHJI dhe HAKJ, përkatësisht. Rezulton se sipërfaqet e këtyre drejtkëndëshave janë saktësisht të barabarta me sipërfaqet e katrorëve të ndërtuar në këmbët përkatëse.

Le të përpiqemi të vërtetojmë se sipërfaqja e katrorit DECA është e barabartë me sipërfaqen e drejtkëndëshit AHJK për ta bërë këtë, ne do të përdorim një vëzhgim ndihmës: Sipërfaqja e një trekëndëshi me të njëjtën lartësi dhe bazë. drejtkëndëshi i dhënë është i barabartë me gjysmën e sipërfaqes së drejtkëndëshit të dhënë. Kjo është pasojë e përcaktimit të zonës së një trekëndëshi si gjysma e produktit të bazës dhe lartësisë. Nga ky vëzhgim rezulton se sipërfaqja e trekëndëshit ACK është e barabartë me sipërfaqen e trekëndëshit AHK (nuk tregohet në figurë), e cila nga ana tjetër është e barabartë me gjysmën e sipërfaqes së drejtkëndëshit AHJK.

Le të vërtetojmë tani se sipërfaqja e trekëndëshit ACK është gjithashtu e barabartë me gjysmën e sipërfaqes së katrorit DECA. E vetmja gjë që duhet bërë për këtë është të vërtetohet barazia e trekëndëshave ACK dhe BDA (pasi sipërfaqja e trekëndëshit BDA është e barabartë me gjysmën e sipërfaqes së katrorit sipas vetive të mësipërme). Kjo barazi është e qartë: trekëndëshat janë të barabartë në të dy anët dhe këndi ndërmjet tyre. Domethënë - AB=AK, AD=AC - barazia e këndeve CAK dhe BAD është e lehtë të vërtetohet me metodën e lëvizjes: ne e rrotullojmë trekëndëshin CAK 90° në drejtim të kundërt të akrepave të orës, atëherë është e qartë se brinjët përkatëse të dy trekëndëshave në pyetja do të përkojë (për faktin se këndi në kulmin e katrorit është 90°).

Arsyetimi për barazinë e sipërfaqeve të katrorit BCFG dhe drejtkëndëshit BHJI është plotësisht i ngjashëm.

Kështu, ne vërtetuam se sipërfaqja e një katrori të ndërtuar mbi hipotenuzë është e përbërë nga sipërfaqet e katrorëve të ndërtuar mbi këmbët. Ideja pas kësaj prove ilustrohet më tej nga animacioni i mësipërm.

Dëshmi e Leonardo da Vinçit

Elementet kryesore të provës janë simetria dhe lëvizja.

Le të shqyrtojmë vizatimin, siç shihet nga simetria, segmenti e pret katrorin në dy pjesë identike (pasi trekëndëshat janë të barabartë në ndërtim).

Duke përdorur një rrotullim 90 gradë në të kundërt të akrepave të orës rreth pikës, ne shohim barazinë e figurave të hijezuara dhe.

Tani është e qartë se sipërfaqja e figurës që kemi hijezuar është e barabartë me shumën e gjysmës së sipërfaqeve të katrorëve të vegjël (të ndërtuar në këmbë) dhe sipërfaqes së trekëndëshit origjinal. Nga ana tjetër, është e barabartë me gjysmën e sipërfaqes së katrorit të madh (të ndërtuar mbi hipotenuzë) plus sipërfaqen e trekëndëshit origjinal. Kështu, gjysma e shumës së sipërfaqeve të katrorëve të vegjël është e barabartë me gjysmën e sipërfaqes së katrorit të madh, dhe për këtë arsye shuma e sipërfaqeve të katrorëve të ndërtuar në këmbë është e barabartë me sipërfaqen e katrorit të ndërtuar në hipotenuzë.

Vërtetimi me metodën e pafundme

Prova e mëposhtme duke përdorur ekuacione diferenciale i atribuohet shpesh matematikanit të famshëm anglez Hardy, i cili jetoi në gjysmën e parë të shekullit të 20-të.

Duke parë vizatimin e paraqitur në figurë dhe duke vëzhguar ndryshimin në anë a, mund të shkruajmë relacionin e mëposhtëm për inkretime anësore pafundësisht të vogla Me Dhe a(duke përdorur ngjashmërinë e trekëndëshit):

Duke përdorur metodën e ndarjes së variablave, gjejmë

Një shprehje më e përgjithshme për ndryshimin e hipotenuzës në rastin e rritjeve në të dyja anët

Integrimi ekuacioni i dhënë dhe duke përdorur kushtet fillestare, marrim

Kështu arrijmë në përgjigjen e dëshiruar

Siç shihet lehtë, varësia kuadratike në formulën përfundimtare shfaqet për shkak të proporcionalitetit linear midis brinjëve të trekëndëshit dhe rritjeve, ndërsa shuma shoqërohet me kontribute të pavarura nga rritja e këmbëve të ndryshme.

Një provë më e thjeshtë mund të merret nëse supozojmë se njëra nga këmbët nuk përjeton një rritje (në këtë rast këmba). Pastaj për konstantën e integrimit marrim

Variacione dhe përgjithësime

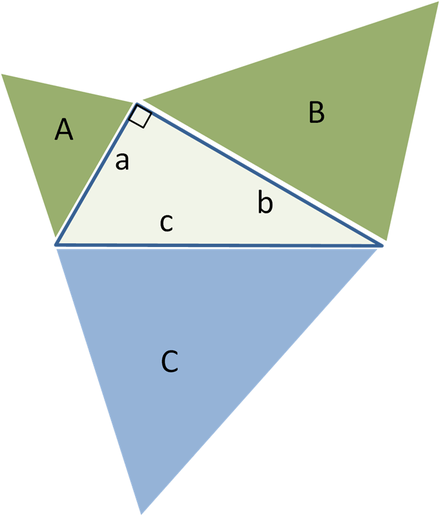
Forma të ngjashme gjeometrike në tre anët

Përgjithësim për trekëndësha të ngjashëm, zona e formave të gjelbra A + B = zona e blu C

Teorema e Pitagorës duke përdorur trekëndësha të ngjashëm kënddrejtë

Euklidi përgjithësoi teoremën e Pitagorës në veprën e tij Fillimet, duke zgjeruar sipërfaqet e katrorëve në anët në zona të ngjashme forma gjeometrike :

Nëse ndërtojmë figura të ngjashme gjeometrike (shih gjeometrinë Euklidiane) në anët e një trekëndëshi kënddrejtë, atëherë shuma e dy figurave më të vogla do të jetë e barabartë me sipërfaqen e figurës më të madhe.

Ideja kryesore e këtij përgjithësimi është se zona e një figure të tillë gjeometrike është në përpjesëtim me katrorin e cilësdo prej dimensioneve të saj lineare dhe, në veçanti, me katrorin e gjatësisë së çdo ane. Prandaj, për shifra të ngjashme me katrorë A, B Dhe C ndërtuar në faqe me gjatësi a, b Dhe c, kemi:

Por, sipas teoremës së Pitagorës, a 2 + b 2 = c 2 pastaj A + B = C.

Në të kundërt, nëse mund ta vërtetojmë këtë A + B = C për tre figura gjeometrike të ngjashme pa përdorur teoremën e Pitagorës, atëherë mund të vërtetojmë vetë teoremën duke lëvizur në drejtim i kundërt. Për shembull, trekëndëshi i qendrës fillestare mund të ripërdoret si trekëndësh C në hipotenuzë dhe dy trekëndësha kënddrejtë të ngjashëm ( A Dhe B), të ndërtuara në dy anët e tjera, të cilat formohen duke ndarë trekëndëshin qendror me lartësinë e tij. Shuma e dy zonave më të vogla të trekëndëshave është padyshim e barabartë me sipërfaqen e trekëndëshit, pra A + B = C dhe, duke përmbushur provën e mëparshme në rend i kundërt, marrim teoremën e Pitagorës a 2 + b 2 = c 2 .

Teorema e kosinusit

Teorema e Pitagorës është rast i veçantë një teoremë më e përgjithshme e kosinuseve, e cila lidh gjatësitë e brinjëve në një trekëndësh arbitrar:

ku θ është këndi ndërmjet brinjëve a Dhe b.

Nëse θ është 90 gradë atëherë cos θ = 0 dhe formula thjeshtohet me teoremën e zakonshme të Pitagorës.

Trekëndëshi i lirë

Në çdo cep të zgjedhur të një trekëndëshi arbitrar me brinjë a, b, c shkruaj një trekëndësh dykëndësh në mënyrë të tillë që kënde të barabarta në bazën e tij θ ishte e barabartë me këndin e zgjedhur. Le të supozojmë se këndi i zgjedhur θ ndodhet përballë anës së caktuar c. Si rezultat, kemi marrë trekëndëshin ABD me kënd θ, i cili ndodhet përballë anës a dhe partitë r. Trekëndëshi i dytë formohet nga këndi θ, i cili ndodhet përballë anës b dhe partitë Me gjatësia s siç tregohet në foto. Thabit Ibn Kurra argumentoi se brinjët në këta tre trekëndësha lidhen si vijon:

Kur këndi θ i afrohet π/2, baza trekëndëshi dykëndësh zvogëlohet dhe të dy anët r dhe s mbivendosen gjithnjë e më pak. Kur θ = π/2, ADB bëhet një trekëndësh kënddrejtë, r + s = c dhe marrim teoremën fillestare të Pitagorës.

Le të shqyrtojmë një nga argumentet. Trekëndëshi ABC ka të njëjtat kënde si trekëndëshi ABD, por në rend të kundërt. (Dy trekëndëshat kanë një kënd të përbashkët në kulmin B, të dy kanë një kënd θ dhe gjithashtu kanë të njëjtin kënd të tretë, bazuar në shumën e këndeve të trekëndëshit) Prandaj, ABC është i ngjashëm me reflektimin ABD të trekëndëshit DBA, si treguar në figurën e poshtme. Le të shkruajmë marrëdhënien ndërmjet anët e kundërta dhe ngjitur me këndin θ,

Gjithashtu një pasqyrim i një trekëndëshi tjetër,

Le të shumëzojmë thyesat dhe të mbledhim këto dy raporte:

Q.E.D.

Përgjithësim për trekëndëshat arbitrarë nëpërmjet paralelogrameve

Përgjithësim për trekëndësha arbitrare,
zonë e gjelbër parcelë = sipërfaqe blu

Vërtetim i tezës se në figurën e mësipërme

Le të bëjmë një përgjithësim të mëtejshëm për trekëndëshat jo kënddrejtë duke përdorur paralelogramë në tre brinjë në vend të katrorëve. (katroret janë një rast i veçantë.) Figura e sipërme tregon se për trekëndëshi akut zona e një paralelogrami për anën e gjatë e barabartë me shumën e paralelogrameve në dy anët e tjera, me kusht që paralelogrami në anën e gjatë të jetë i ndërtuar siç tregohet në figurë (përmasat e shënuara me shigjeta janë të njëjta dhe përcaktojnë anët e paralelogramit të poshtëm). Ky zëvendësim i katrorëve me paralelogramë ka një ngjashmëri të qartë me teoremën fillestare të Pitagorës, që mendohet se është formuluar nga Pappus i Aleksandrisë në vitin 4 pas Krishtit. e.

Figura e poshtme tregon ecurinë e provës. Le të shohim anën e majtë të trekëndëshit. Paralelogrami i gjelbër i majtë ka të njëjtën sipërfaqe si anën e majtë paralelogrami blu sepse kanë të njëjtën bazë b dhe lartësia h. Gjithashtu, paralelogrami i gjelbër i majtë ka të njëjtën zonë si paralelogrami i gjelbër i majtë në foton e sipërme sepse ato kanë terren të përbashkët(ana e sipërme e majtë e trekëndëshit) dhe lartësia totale pingul me atë anë të trekëndëshit. Duke përdorur arsyetime të ngjashme për anën e djathtë të trekëndëshit, do të vërtetojmë se paralelogrami i poshtëm ka të njëjtën sipërfaqe me dy paralelogramet jeshile.

Numrat kompleks

Teorema e Pitagorës përdoret për të gjetur distancën midis dy pikave në një sistem koordinativ kartezian, dhe kjo teoremë është e vlefshme për të gjitha koordinatat e vërteta: distancën s mes dy pikave ( a, b) Dhe ( c,d) barazohet

Nuk ka probleme me formulën nëse numrat kompleks trajtohen si vektorë me komponentë realë x + unë y = (x, y). . Për shembull, distanca s ndërmjet 0 + 1 i dhe 1 + 0 i llogaritur si modul i vektorit (0, 1) − (1, 0) = (−1, 1), ose

Sidoqoftë, për veprimet me vektorë me koordinata komplekse, është e nevojshme të bëhen përmirësime të caktuara në formulën e Pitagorës. Largësia ndërmjet pikave me numra komplekse (a, b) Dhe ( c, d); a, b, c, Dhe d të gjitha komplekse, ne i formulojmë duke përdorur vlera absolute. Largësia s bazuar në dallimi vektorial (a − c, b − d) V formën e mëposhtme: le dallimin a − c = fq+i q, Ku fq - pjesë reale dallimet qështë pjesa imagjinare, dhe i = √(−1). Po kështu, le b − d = r+i s. Pastaj:

ku është numri kompleks i konjuguar për . Për shembull, distanca midis pikave (a, b) = (0, 1) Dhe (c, d) = (i, 0) , le të llogarisim diferencën (a − c, b − d) = (−i, 1) dhe rezultati do të ishte 0 nëse nuk do të përdoreshin konjugatet komplekse. Prandaj, duke përdorur formulën e përmirësuar, marrim

Moduli është përcaktuar si më poshtë:

Stereometria

Një përgjithësim domethënës i teoremës së Pitagorës për hapësirën tredimensionale është teorema e de Goy, e quajtur sipas J.-P. de Gois: nëse një katërkëndor ka një kënd të drejtë (si në një kub), atëherë katrori i sipërfaqes së fytyrës përballë këndit të duhur është i barabartë me shumën e katrorëve të sipërfaqeve të tre fytyrave të tjera. Ky përfundim mund të përmblidhet si " n-teorema dimensionale e Pitagorës":

Teorema e Pitagorës hapësirë ​​tredimensionale lidh diagonalen AD me tre anët.

Një përgjithësim tjetër: Teorema e Pitagorës mund të zbatohet për stereometrinë në formën e mëposhtme. Le të shqyrtojmë kuboid siç tregohet në foto. Le të gjejmë gjatësinë e diagonales BD duke përdorur teoremën e Pitagorës:

ku të tre brinjët formojnë një trekëndësh kënddrejtë. Ne përdorim diagonalen horizontale BD dhe skajin vertikal AB për të gjetur gjatësinë e diagonales AD, për këtë ne përsëri përdorim teoremën e Pitagorës:

ose, nëse shkruajmë gjithçka në një ekuacion:

Ky rezultat është një shprehje tredimensionale për përcaktimin e madhësisë së vektorit v(diagonale AD), e shprehur në termat e përbërësve të saj pingulë ( v k ) (tre reciprokisht brinjë pingule):

Ky ekuacion mund të konsiderohet si një përgjithësim i teoremës së Pitagorës për hapësirë ​​shumëdimensionale. Megjithatë, rezultati në të vërtetë nuk është asgjë më shumë se aplikimi i përsëritur i teoremës së Pitagorës në një sekuencë trekëndëshash kënddrejtë në plane të njëpasnjëshme pingul.

Hapësirë ​​vektoriale

Në rastin e një sistemi ortogonal vektorësh, ekziston një barazi, e cila quhet edhe teorema e Pitagorës:

Nëse është projeksioni i vektorit mbi boshtet e koordinatave, atëherë kjo formulë përkon me distancën Euklidiane - dhe do të thotë se gjatësia e vektorit është e barabartë me rrënjën katrore të shumës së katrorëve të përbërësve të tij.

Analogu i kësaj barazie në rastin e një sistemi të pafund vektorësh quhet barazia e Parsevalit.

Gjeometria jo-Euklidiane

Teorema e Pitagorës rrjedh nga aksiomat e gjeometrisë Euklidiane dhe, në fakt, nuk vlen për gjeometrinë jo-Euklidiane, në formën në të cilën është shkruar më sipër. (Dmth, teorema e Pitagorës rezulton të jetë një lloj ekuivalenti me postulatin e paralelizmit të Euklidit) Me fjalë të tjera, në gjeometrinë jo-Euklidiane marrëdhënia midis brinjëve të një trekëndëshi do të jetë domosdoshmërisht në një formë të ndryshme nga teorema e Pitagorës. Për shembull, në gjeometrinë sferike, të tre anët e një trekëndëshi kënddrejtë (të themi a, b Dhe c), të cilat kufizojnë oktantin (pjesën e tetë) të sferës njësi, kanë një gjatësi π/2, që bie ndesh me teoremën e Pitagorës, sepse a 2 + b 2 ≠ c 2 .

Le të shqyrtojmë këtu dy raste të gjeometrisë jo-Euklidiane - gjeometria sferike dhe hiperbolike; në të dyja rastet, si për hapësirën Euklidiane për trekëndëshat kënddrejtë, rezultati, i cili zëvendëson teoremën e Pitagorës, rrjedh nga teorema e kosinusit.

Megjithatë, teorema e Pitagorës mbetet e vlefshme për gjeometrinë hiperbolike dhe eliptike nëse kërkesa që trekëndëshi të jetë drejtkëndësh zëvendësohet me kushtin që shuma e dy këndeve të trekëndëshit duhet të jetë e barabartë me të tretin, të themi. A+B = C. Atëherë marrëdhënia midis anëve duket kështu: shuma e sipërfaqeve të rrathëve me diametër a Dhe b e barabartë me sipërfaqen e një rrethi me diametër c.

Gjeometria sferike

Për çdo trekëndësh kënddrejtë në një sferë me rreze R(për shembull, nëse këndi γ në një trekëndësh është i drejtë) me brinjë a, b, c Marrëdhënia midis palëve do të duket si kjo:

Kjo barazi mund të nxirret si një rast i veçantë i teoremës sferike të kosinusit, e cila është e vlefshme për të gjithë trekëndëshat sferikë:

ku është cosh kosinus hiperbolik. Kjo formulë është një rast i veçantë i teoremës hiperbolike të kosinusit, e cila është e vlefshme për të gjithë trekëndëshat:

ku γ është këndi kulmi i të cilit është i kundërt me brinjën c.

Ku g ij quhet tensor metrikë. Mund të jetë funksion i pozicionit. Hapësira të tilla kurvilineare përfshijnë gjeometrinë Riemanniane si një shembull të përgjithshëm. Ky formulim është gjithashtu i përshtatshëm për hapësirën Euklidiane kur përdoren koordinatat kurvilineare. Për shembull, për koordinatat polare:

Vepra arti vektoriale

Teorema e Pitagorës lidh dy shprehje të sasisë produkt vektorial. Një qasje për përcaktimin e një produkti kryq kërkon që ai të përmbushë ekuacionin:

kjo formulë përdor produktin me pika. Ana e djathte ekuacioni quhet përcaktor Gram për a Dhe b, e cila është e barabartë me sipërfaqen e paralelogramit të formuar nga këta dy vektorë. Bazuar në këtë kërkesë, si dhe kërkesën që produkti vektor të jetë pingul me përbërësit e tij a Dhe b rrjedh se, përveç rasteve të parëndësishme nga hapësira 0- dhe 1-dimensionale, prodhimi kryq përcaktohet vetëm në tre dhe shtatë dimensione. Ne përdorim përkufizimin e këndit në n- hapësirë ​​dimensionale:

Kjo veti e një produkti kryq e jep madhësinë e tij si më poshtë:

Përmes identitetit themelor trigonometrik të Pitagorës marrim një formë tjetër të shkrimit të vlerës së tij:

Një qasje alternative për përcaktimin e një produkti kryq është përdorimi i një shprehjeje për madhësinë e tij. Pastaj, duke arsyetuar në rend të kundërt, marrim një lidhje me produkt skalar:

Shihni gjithashtu

Shënime

1. Tema e historisë: Teorema e Pitagorës në matematikën babilonase
2. ( , fq. 351) fq
3. ( , Vëllimi I, f. 144)
4. Një diskutim i fakteve historike jepet në (, F. 351) F. 351
5. Kurt Von Fritz (prill, 1945). "Zbulimi i pakrahasueshmërisë nga Hipasus i Metapontum". Analet e Matematikës, Seria e Dytë(Analet e Matematikës) 46 (2): 242–264.
6. Lewis Carroll, “The Story with Knots”, M., Mir, 1985, f. 7
7. Asger Aaboe Episode nga historia e hershme e matematikës. - Shoqata Matematikore e Amerikës, 1997. - F. 51. - ISBN 0883856131
8. Propozim Python nga Elisha Scott Loomis
9. Euklidit Elementet: Libri VI, Pohimi VI 31: “Në trekëndëshat kënddrejtë, figura në anën që nënshtron këndin e drejtë është e barabartë me figurat e ngjashme dhe të përshkruara në mënyrë të ngjashme në brinjët që përmbajnë këndin e duhur.”
10. Lawrence S. Leff punë e cituar. - Seria edukative e Barron - F. 326. - ISBN 0764128922
11. Howard Whitley Eves§4.8:...përgjithësimi i teoremës së Pitagorës // Momente të mëdha në matematikë (para vitit 1650). - Shoqata Matematikore e Amerikës, 1983. - F. 41. - ISBN 0883853108
12. Tâbit ibn Qorra (emri i plotë Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 pas Krishtit) ishte një mjek që jetonte në Bagdad i cili shkroi gjerësisht mbi Elementet e Euklidit dhe të tjerë lëndët matematikore.
13. Aydin Sayili (mars 1960). Përgjithësimi i Teoremës së Pitagorës nga Thâbit ibn Qurra. Isis 51 (1): 35–37. DOI: 10.1086/348837.
14. Judith D. Sally, Paul Sally Ushtrimi 2.10 (ii) // Vepër e cituar. - F. 62. - ISBN 0821844032
15. Për detajet e një ndërtimi të tillë, shih George Jennings Figura 1.32: Teorema e përgjithësuar e Pitagorës // Gjeometria moderne me aplikime: me 150 figura. - 3. - Springer, 1997. - F. 23. - ISBN 038794222X
16. Arlen Brown, Carl M. Pearcy Artikulli C: Norma për një arbitrar n-tuple ... // Një hyrje në analizë . - Springer, 1995. - F. 124. - ISBN 0387943692 Shihni gjithashtu faqet 47-50.
17. Alfred Grey, Elsa Abbena, Simon Salamon Gjeometria diferenciale moderne e kthesave dhe sipërfaqeve me Mathematica. - 3. - CRC Press, 2006. - F. 194. - ISBN 1584884487
18. Rajendra Bhatia Analiza e matricës. - Springer, 1997. - F. 21. - ISBN 0387948465
19. Stephen W. Hawking punë e cituar. - 2005. - F. 4. - ISBN 0762419229
20. Eric W. Weiststein CRC enciklopedi koncize e matematikës. - 2. - 2003. - F. 2147. - ISBN 1584883472
21. Alexander R. Pruss

Historia e teoremës së Pitagorës daton disa mijëra vjet. Një deklaratë që thotë se dihej shumë kohë përpara lindjes së matematikanit grek. Sidoqoftë, teorema e Pitagorës, historia e krijimit dhe vërtetimi i saj janë të lidhura për shumicën me këtë shkencëtar. Sipas disa burimeve, arsyeja për këtë ishte prova e parë e teoremës, e cila u dha nga Pitagora. Megjithatë, disa studiues e mohojnë këtë fakt.

Muzika dhe logjika

Para se të tregojmë se si u zhvillua historia e teoremës së Pitagorës, le të shohim shkurtimisht biografinë e matematikanit. Ai jetoi në shekullin e 6 para Krishtit. Data e lindjes së Pitagorës konsiderohet të jetë 570 para Krishtit. e., vendi është ishulli i Samos. Pak dihet me besueshmëri për jetën e shkencëtarit. Të dhënat biografike në burimet e lashta greke janë të ndërthurura me trillime të dukshme. Në faqet e traktateve, ai shfaqet si një i urtë i madh me zotërim të shkëlqyeshëm të fjalëve dhe aftësi për të bindur. Nga rruga, kjo është arsyeja pse matematikani grek u mbiquajtur Pitagora, domethënë "fjalim bindës". Sipas një versioni tjetër, lindja e të urtit të ardhshëm u parashikua nga Pythia. Babai e quajti djalin Pitagora për nder të saj.

I urti mësoi nga mendjet e mëdha të kohës. Midis mësuesve të Pitagorës së re janë Hermodamantus dhe Pherecydes nga Siros. E para i nguliti dashurinë për muzikën, e dyta i mësoi filozofinë. Të dyja këto shkenca do të mbeten në fokus të shkencëtarit gjatë gjithë jetës së tij.

30 vjet trajnim

Sipas një versioni, duke qenë një i ri kureshtar, Pitagora u largua nga atdheu i tij. Ai shkoi për të kërkuar dije në Egjipt, ku qëndroi, sipas burime të ndryshme, nga 11 deri në 22 vjeç, dhe më pas u kap dhe u dërgua në Babiloni. Pitagora ishte në gjendje të përfitonte nga pozicioni i tij. Për 12 vjet ai studioi matematikë, gjeometri dhe magji në shtet i lashtë. Pitagora u kthye në Samos vetëm në moshën 56-vjeçare. Në atë kohë këtu sundonte tirani Polikrat. Pitagora nuk mund ta pranonte të tillë sistemi politik dhe shpejt shkoi në jug të Italisë, ku ndodhej koloni greke Croton.

Sot është e pamundur të thuhet me siguri nëse Pitagora ishte në Egjipt dhe Babiloni. Ai mund të ketë lënë Samos më vonë dhe shkoi direkt në Croton.

pitagorasit

Historia e teoremës së Pitagorës është e lidhur me zhvillimin e shkollës së krijuar nga filozofi grek. Kjo vëllazëri fetare dhe etike predikonte respektimin e një mënyre të veçantë jetese, studionte aritmetikën, gjeometrinë dhe astronominë dhe merrej me studimin e anës filozofike dhe mistike të numrave.

Të gjitha zbulimet e studentëve të matematikanit grek iu atribuuan atij. Sidoqoftë, historia e shfaqjes së teoremës së Pitagorës lidhet nga biografët e lashtë vetëm me vetë filozofin. Supozohet se ai ua kaloi grekëve njohuritë e marra në Babiloni dhe Egjipt. Ekziston gjithashtu një version që ai në të vërtetë zbuloi teoremën mbi marrëdhëniet midis këmbëve dhe hipotenuzës, pa ditur për arritjet e popujve të tjerë.

Teorema e Pitagorës: historia e zbulimit

Disa burime të lashta greke përshkruajnë gëzimin e Pitagorës kur arriti të provonte teoremën. Për nder të kësaj ngjarje, ai urdhëroi një flijim për perënditë në formën e qindra demave dhe mbajti një festë. Megjithatë, disa shkencëtarë theksojnë pamundësinë e një akti të tillë për shkak të veçorive të pikëpamjeve të Pitagorianëve.

Besohet se në traktatin "Elementet", krijuar nga Euklidi, autori jep një provë të teoremës, autori i së cilës ishte matematikani i madh grek. Sidoqoftë, jo të gjithë e mbështetën këtë këndvështrim. Kështu, edhe filozofi i lashtë neoplatonist Proclus vuri në dukje se autori i provës së dhënë në Elementet ishte vetë Euklidi.

Sido që të jetë, personi i parë që formuloi teoremën nuk ishte Pitagora.

Egjipti i lashtë dhe Babilonia

Teorema e Pitagorës, historia e së cilës diskutohet në artikull, sipas matematikanit gjerman Cantor, ishte e njohur në vitin 2300 para Krishtit. e. në Egjipt. Banorët e lashtë të Luginës së Nilit gjatë mbretërimit të Faraonit Amenemhat I njihnin barazinë 3 2 + 4 ² = 5 ². Supozohet se me ndihmën e trekëndëshave me brinjët 3, 4 dhe 5, "tërheqësit e litarit" egjiptianë ndërtuan kënde të drejta.

Ata e dinin gjithashtu teoremën e Pitagorës në Babiloni. Në pllaka balte që datojnë në 2000 para Krishtit. dhe që daton që nga koha e mbretërimit, u zbulua një llogaritje e përafërt e hipotenuzës së një trekëndëshi kënddrejtë.

India dhe Kina

Historia e teoremës së Pitagorës është gjithashtu e lidhur me qytetërimet e lashta të Indisë dhe Kinës. Traktati "Zhou-bi suan jin" përmban indikacione se (anët e tij janë të lidhura si 3:4:5) ishte i njohur në Kinë që në shekullin e 12-të. para Krishtit e., dhe nga shekulli i 6-të. para Krishtit e. matematikanët e këtij shteti e dinin pamje e përgjithshme teorema.

Ndërtimi i një këndi të drejtë duke përdorur Trekëndëshi egjiptian u deklarua gjithashtu në traktatin indian "Sulva Sutra", që daton në shekujt VII-V. para Krishtit e.

Kështu, historia e teoremës së Pitagorës deri në kohën e lindjes së matematikanit dhe filozofit grek ishte tashmë disa qindra vjeçare.

Dëshmi

Gjatë ekzistencës së saj, teorema u bë një nga ato themelore në gjeometri. Historia e vërtetimit të teoremës së Pitagorës ndoshta filloi me shqyrtimin e një katrori barabrinjës në hipotenuzën dhe këmbët e tij. Ai që "u rrit" në hipotenuzë do të përbëhet nga katër trekëndësha të barabartë me të parin. Sheshet në anët përbëhen nga dy trekëndësha të tillë. E thjeshtë imazh grafik tregon qartë vlefshmërinë e pohimit të formuluar në formën e teoremës së famshme.

Një tjetër provë e thjeshtë kombinon gjeometrinë me algjebrën. Katër trekëndësha identikë kënddrejtë me brinjë a, b, c janë vizatuar në mënyrë që të formojnë dy katrorë: të jashtëm me brinjë (a + b) dhe të brendshëm me brinjë c. Në këtë rast, sipërfaqja e katrorit më të vogël do të jetë e barabartë me c 2. Sipërfaqja e katrorit të madh llogaritet nga shuma e sipërfaqeve të katrorit të vogël dhe të gjithë trekëndëshave (sipërfaqja e një trekëndëshi kënddrejtë, kujtojmë, llogaritet me formulën (a * b) / 2), që është, c 2 + 4 * ((a * b) / 2), që është e barabartë me c 2 + 2av. Sipërfaqja e një katrori të madh mund të llogaritet në një mënyrë tjetër - si produkt i dy anëve, domethënë (a + b) 2, që është e barabartë me një 2 + 2ab + b 2. Rezulton:

a 2 + 2ab + b 2 = c 2 + 2ab,

a 2 + b 2 = c 2.

Ka shumë versione të vërtetimit të kësaj teoreme. Euklidi, shkencëtarët indianë dhe Leonardo da Vinci punuan mbi to. Shpesh dijetarët e lashtë citonin vizatime, shembuj të të cilave ndodhen më lart, dhe nuk i shoqëruan me ndonjë shpjegim tjetër përveç shënimit "Shiko!" Thjeshtësia vërtetim gjeometrik me kusht që të kishit njohuri dhe të mos keni kërkuar komente.

Historia e teoremës së Pitagorës, e përshkruar shkurtimisht në artikull, hedh poshtë mitin për origjinën e saj. Sidoqoftë, është e vështirë edhe të imagjinohet që emri i matematikanit dhe filozofit të madh grek do të pushojë ndonjëherë së lidhuri me të.

Artikulli i mëparshëm: Sa është shpejtësia e dritës Artikulli vijues: Lëkundjet harmonike Formula e fizikës së frekuencës së lëkundjeve