Thjesht diçka e ndërlikuar: numra kompleks. Mundësia e përdorimit të numrave kompleksë në një kurs matematike të shkollës së mesme

• Ne do të bazojmë në lidhje, jo në formula mekanike.
• Le t'i konsiderojmë numrat kompleksë si plotësues të sistemit tonë të numrave, të njëjtë me numrat zero, thyesorë ose negativë.
• I vizualizojmë idetë në grafikë për të kuptuar më mirë thelbin, dhe jo vetëm t'i paraqesim ato në tekst të thatë.

Dhe arma jonë sekrete: të mësuarit me analogji. Ne do të arrijmë te numrat kompleksë duke filluar me paraardhësit e tyre, numra negativë. Këtu është një udhëzues i vogël për ju:

Për momentin, kjo tabelë ka pak kuptim, por le të jetë atje. Në fund të artikullit gjithçka do të bjerë në vend.

Le të kuptojmë vërtet se çfarë janë numrat negativë

Numrat negativë nuk janë aq të thjeshtë. Imagjinoni që jeni një matematikan evropian në shekullin e 18-të. Ju keni 3 dhe 4, dhe mund të shkruani 4 – 3 = 1. Është e thjeshtë.

Por çfarë është 3-4? Çfarë do të thotë saktësisht kjo? Si mund të largoni 4 lopë nga 3? Si mund të kesh më pak se asgjë?

Numrat negativë shiheshin si absurditet të plotë, diçka që "hedhi një hije mbi të gjithë teorinë e ekuacioneve" (Francis Maceres, 1759). Sot do të ishte e pakuptimtë të mendosh për numrat negativë si diçka të palogjikshme dhe të padobishme. Pyete mësuesin nëse numrat negativ shkelin matematikën bazë.

Çfarë ndodhi? Ne shpikëm një numër teorik që kishte veti të dobishme. Numrat negativë nuk mund të preken apo ndjehen, por ata janë të mirë në përshkrimin e marrëdhënieve të caktuara (si borxhi, për shembull). Kjo është një ide shumë e dobishme.

Në vend që të them, "Të kam borxh 30" dhe të lexoj fjalët për të parë nëse jam në të zezë apo në të zezë, thjesht mund të shkruaj "-30" dhe të di se çfarë do të thotë kjo. Nëse fitoj para dhe paguaj borxhet e mia (-30 + 100 = 70), mund ta shkruaj lehtësisht këtë transaksion me disa karaktere. Do të mbetem me +70.

Shenjat plus dhe minus kapin automatikisht drejtimin - nuk ju nevojitet një fjali e tërë për të përshkruar ndryshimet pas çdo transaksioni. Matematika është bërë më e thjeshtë, më elegante. Nuk kishte më rëndësi nëse numrat negativë ishin "të prekshëm" - ata kishin veti të dobishme dhe ne i përdorëm ato derisa u vendosën fort në jetën tonë të përditshme. Nëse dikush që njihni nuk e ka kuptuar ende thelbin e numrave negativë, tani mund t'i ndihmoni.

Por le të mos minimizojmë vuajtjet njerëzore: numrat negativë ishin një ndryshim i vërtetë në vetëdije. Edhe Euler, gjeniu që zbuloi numrin e dhe shumë më tepër, nuk i kuptonte numrat negativë si ne sot. Ato shiheshin si rezultate "të pakuptimta" të llogaritjeve.

Është e çuditshme të presësh që fëmijët të kuptojnë me qetësi idetë që dikur ngatërronin edhe matematikanët më të mirë.

Futja e numrave imagjinarë

Është e njëjta histori me numrat imagjinarë. Ne mund të zgjidhim ekuacione të tilla gjatë gjithë ditës:

Përgjigjet do të jenë 3 dhe -3. Por le të imagjinojmë që një djalë i zgjuar shtoi një minus këtu:

Epo, mirë. Kjo është lloji i pyetjes që i bën njerëzit të dridhen kur e shohin për herë të parë. Dëshironi të llogaritni rrënjën katrore të një numri më të vogël se zero? Kjo është e paimagjinueshme! (Historikisht, pyetje të ngjashme ekzistonin në të vërtetë, por është më e përshtatshme për mua të imagjinoj një djalë të mençur pa fytyrë, në mënyrë që të mos turpëroj shkencëtarët e së kaluarës).

Duket e çmendur, ashtu si numrat negativë, zero dhe numrat irracionalë (numrat jopërsëritës) të parë në ditë. Nuk ka asnjë kuptim "të vërtetë" për këtë pyetje, apo jo?

Jo, nuk është e vërtetë. Të ashtuquajturit "numra imagjinarë" janë po aq normalë sa çdo tjetër (ose po aq jonormal): ata janë një mjet për të përshkruar botën. Në të njëjtën frymë që imagjinojmë se -1, 0.3 dhe 0 "ekzistojnë", le të supozojmë se ka një numër i, ku:

Me fjalë të tjera, ju e shumëzoni i me vetveten për të marrë -1. Çfarë po ndodh tani?

Epo, së pari sigurisht që kemi një dhimbje koke. Por duke luajtur lojën "Të pretendojmë se ekzistoj" ne në fakt e bëjmë matematikën më të thjeshtë dhe më elegante. Shfaqen lidhje të reja që mund t'i përshkruajmë lehtësisht.

Ju nuk do të besoni në i, ashtu si ata matematikanët e vjetër inatosur nuk besuan në ekzistencën e -1. Të gjitha konceptet e reja që e kthejnë trurin në një tub janë të vështira për t'u perceptuar dhe kuptimi i tyre nuk shfaqet menjëherë, madje edhe për të shkëlqyerin Euler. Por siç na kanë treguar numrat negativë, idetë e reja të çuditshme mund të jenë jashtëzakonisht të dobishme.

Nuk më pëlqen vetë termi "numra imagjinarë" - duket sikur është zgjedhur posaçërisht për të ofenduar ndjenjat e i. Numri i është po aq normal sa të tjerët, por pseudonimi “imagjinar” i ka mbetur, ndaj do ta përdorim edhe ne.

Kuptimi vizual i numrave negativë dhe kompleksë

Ekuacioni x^2 = 9 në fakt do të thotë këtë:

Cili transformim i x-it, i zbatuar dy herë, e kthen 1 në 9?

Ka dy përgjigje: "x = 3" dhe "x = -3". Kjo do të thotë, ju mund të "shkallëzoni me" 3 herë ose "të shkallëzoni me 3 dhe të rrokullisni" (kthimi ose marrja e kundërt e rezultatit janë të gjitha interpretime të shumëzimit me një negativ).

Tani le të mendojmë për ekuacionin x^2 = -1, i cili mund të shkruhet kështu:

Cili transformim i x-it, i zbatuar dy herë, e kthen 1 në -1? Hm.

• Një numër pozitiv nuk mund ta shumëzojmë dy herë sepse rezultati do të jetë pozitiv.
• Një numër negativ nuk mund ta shumëzojmë dy herë sepse rezultati do të jetë sërish pozitiv.

Po... rotacioni! Tingëllon e pazakontë, sigurisht, por çka nëse e mendojmë x si një "rrotullim 90 gradë", atëherë duke aplikuar x dy herë, do të bëjmë një rrotullim 180 gradë në boshtin e koordinatave dhe 1 do të kthehet në -1!

Uau! Dhe nëse e mendojmë pak më shumë, mund të bëjmë dy rrotullime në drejtim të kundërt, dhe gjithashtu të shkojmë nga 1 në -1. Ky është një rrotullim "negativ" ose shumëzim me -i:

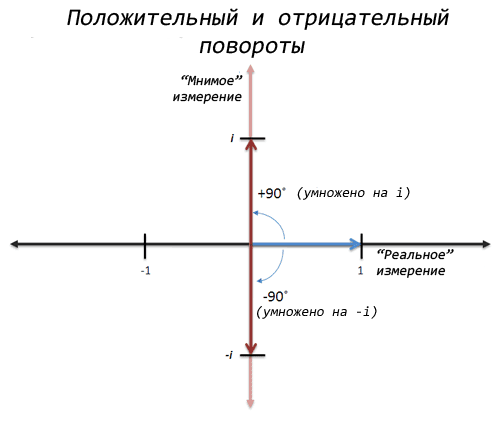
Nëse shumëzojmë me -i dy herë, atëherë në shumëzimin e parë marrim -i nga 1, dhe në të dytin -1 nga -i. Pra, ekzistojnë dy rrënjë katrore të -1: i dhe -i.

Kjo është shumë e lezetshme! Ne kemi diçka si një zgjidhje, por çfarë do të thotë?

• i është "dimensioni i ri imagjinar" për matjen e numrit
• i (ose -i) është ajo që numrat "bëhen" kur rrotullohen
• Duke shumëzuar me i është duke u rrotulluar 90 gradë në të kundërt të akrepave të orës
• Shumëzimi me -i është një rrotullim 90 gradë në drejtim të akrepave të orës.
• Rrotullimi dy herë në secilin drejtim jep -1: na kthen në dimensionin "normal" të numrave pozitivë dhe negativë (boshti x).

Të gjithë numrat janë 2-dimensionale. Po, është e vështirë të pranohet, por romakët e lashtë gjithashtu do ta kishin pasur të vështirë të pranonin numrat dhjetorë ose ndarjen e gjatë. (Si ndodh që ka më shumë numra midis 1 dhe 2?). Duket e çuditshme, si çdo mënyrë e re e të menduarit në matematikë.

Ne pyetëm "Si ta kthejmë 1 në -1 në dy veprime?" dhe gjeti përgjigjen: rrotullohu 1 90 gradë dy herë. Një mënyrë mjaft e çuditshme, e re e të menduarit në matematikë. Por shumë e dobishme. (Nga rruga, ky interpretim gjeometrik i numrave kompleks u shfaq vetëm dekada pas zbulimit të vetë numrit i).

Gjithashtu, mos harroni se pranimi i një rrotullimi në drejtim të kundërt të akrepave të orës si rezultat pozitiv është një konventë thjesht njerëzore dhe gjithçka mund të kishte qenë krejtësisht ndryshe.

Kërkoni për grupe

Le të shkojmë pak më thellë në detaje. Kur shumëzoni numra negativë (si -1), ju merrni një grup:

• 1, -1, 1, -1, 1, -1, 1, -1

Meqenëse -1 nuk ndryshon madhësinë e numrit, por vetëm shenjën, ju merrni të njëjtin numër ose me shenjën "+" ose me shenjën "-". Për numrin x merrni:

• x, -x, x, -x, x, -x…

Kjo është një ide shumë e dobishme. Numri "x" mund të përfaqësojë javë të mira dhe të këqija. Le të imagjinojmë se një javë e mirë pason një të keqe; Është një javë e mirë; Si do të jetë java e 47-të?

X do të thotë se do të jetë një javë e keqe. Shihni se si numrat negativë "ndjekin shenjën" - ne thjesht mund të fusim (-1)^47 në kalkulator në vend që të numërojmë ("Java 1 e mirë, java 2 e keqe... java 3 e mirë..."). Gjërat që alternojnë vazhdimisht mund të modelohen në mënyrë të përsosur duke përdorur numra negativë.

Mirë, çfarë ndodh nëse vazhdojmë të shumëzojmë me i?

Shumë qesharake, le t'i thjeshtojmë pak të gjitha:

Këtu është e njëjta gjë e paraqitur grafikisht:

Ne e përsërisim ciklin çdo kthesë të 4-të. Kjo padyshim ka kuptim, apo jo? Çdo fëmijë do t'ju thotë se 4 kthesat në të majtë janë njësoj si të mos ktheheni fare. Tani bëni një pushim nga numrat imagjinarë (i, i^2) dhe shikoni grupin total:

• X, Y, -X, -Y, X, Y, -X, -Y…

Ashtu si numrat negativë modelojnë imazhin pasqyrues të numrave, numrat imagjinarë mund të modelojnë çdo gjë që rrotullohet midis dy dimensioneve "X" dhe "Y". Ose ndonjë gjë me një varësi ciklike, rrethore - a keni ndonjë gjë në mendje?

Kuptimi i numrave kompleks

Ekziston edhe një detaj tjetër për t'u marrë parasysh: a mund të jetë një numër edhe "real" dhe "imagjinar"?

As mos e dyshoni. Kush tha që duhet të kthehemi saktësisht 90 gradë? Nëse qëndrojmë me njërën këmbë në dimensionin "real" dhe tjetrën në atë "imagjinare", do të duket diçka si kjo:

Jemi në shenjën 45 gradë, ku pjesët reale dhe imagjinare janë të njëjta, dhe vetë numri është "1 + i". Është si një hot dog, ku ka edhe ketchup dhe mustardë – kush tha që duhet të zgjidhni njërën apo tjetrën?

Në thelb, ne mund të zgjedhim çdo kombinim të pjesëve reale dhe imagjinare dhe të bëjmë një trekëndësh nga e gjithë kjo. Këndi bëhet "këndi i rrotullimit". Një numër kompleks është një emër i zbukuruar për numrat që kanë një pjesë reale dhe një pjesë imagjinare. Ato shkruhen si "a + bi", ku:

• a - pjesë reale
• b - pjesa imagjinare

Jo keq. Por një pyetje e fundit mbetet: sa "i madh" është një numër kompleks? Nuk mund të matim veçmas pjesën reale apo imagjinare, sepse do të humbasim pamjen e madhe.

Le të bëjmë një hap prapa. Madhësia e një numri negativ është distanca nga zero:

Kjo është një mënyrë tjetër për të gjetur vlerën absolute. Por si të maten të dy komponentët në 90 gradë për numrat kompleks?

A është zog në qiell... apo aeroplan... Pitagora po vjen në shpëtim!

Kjo teoremë shfaqet kudo që është e mundur, madje edhe në numra të shpikur 2000 vjet pas vetë teoremës. Po, ne po bëjmë një trekëndësh dhe hipotenuza e tij do të jetë e barabartë me distancën nga zero:

Ndërsa matja e një numri kompleks nuk është aq e thjeshtë sa "vetëm heqja e shenjës -", ​​numrat kompleksë kanë disa përdorime shumë të dobishme. Le të shohim disa prej tyre.

Shembull real: Rrotullimet

Ne nuk do të presim derisa fizika e kolegjit të praktikojë numrat kompleksë. Ne do ta bëjmë këtë sot. Mund të thuhet shumë për temën e shumëzimit të numrave kompleksë, por tani për tani ju duhet të kuptoni gjënë kryesore:

• Shumëzimi me një numër kompleks rrotullohet me këndin e tij

Le të shohim se si funksionon. Imagjinoni që jam në një varkë, duke lëvizur në një kurs prej 3 njësive në Lindje çdo 4 njësi në Veri. Unë dua të ndryshoj kursin tim 45 gradë në të kundërt të akrepave të orës. Cili do të jetë kursi im i ri?

Dikush mund të thotë “Është e lehtë! Llogarit sinusin, kosinusin, google vlerën tangjente... dhe më pas..." Mendoj se e prisha kalkulatorin...

Le të marrim një rrugë më të thjeshtë: jemi në një kurs 3 + 4i (nuk ka rëndësi se cili është këndi, nuk na intereson tani për tani) dhe duam të kthehemi 45 gradë. Epo, 45 gradë është 1 + i (diagonale ideale). Kështu që ne mund ta shumëzojmë normën tonë me këtë numër!

Këtu është thelbi:

• Titulli fillestar: 3 njësi Lindje, 4 njësi Veri = 3 + 4i
• Rrotulloni në drejtim të kundërt të akrepave të orës 45 gradë = shumëzojeni me 1 + i

Kur shumëzojmë marrim:

Udhëzuesi ynë i ri është 1 njësi në perëndim (-1 në lindje) dhe 7 njësi në veri, ju mund të vizatoni koordinatat në grafik dhe t'i ndiqni ato.

Por! Përgjigjen e gjetëm në 10 sekonda, pa asnjë sinus dhe kosinus. Nuk kishte vektorë, as matrica, as gjurmim se në cilin kuadrant ishim. Ishte aritmetikë e thjeshtë dhe pak algjebër për të përpunuar ekuacionin. Numrat imagjinarë janë të shkëlqyeshëm për rrotullim!

Për më tepër, rezultati i një llogaritjeje të tillë është shumë i dobishëm. Ne kemi kursin (-1, 7) në vend të këndit (atan(7/-1) = 98,13, dhe është menjëherë e qartë se jemi në kuadrantin e dytë. Si, saktësisht, keni planifikuar të vizatoni dhe ndiqni këndin e treguar Përdorimi i një raportuesi në dorë?

Jo, ju do ta ktheni këndin në kosinus dhe sinus (-0,14 dhe 0,99), do të gjenit raportin e përafërt midis tyre (rreth 1 me 7) dhe do të skiconit një trekëndësh. Dhe këtu numrat kompleksë fitojnë padyshim - saktë, rrufe të shpejtë dhe pa kalkulator!

Nëse jeni si unë, do ta gjeni mendjemprehtë këtë zbulim. Nëse jo, kam frikë se matematika nuk të emocionon fare. Na vjen keq!

Trigonometria është e mirë, por numrat kompleksë i bëjnë llogaritjet shumë më të lehta (si gjetja e cos(a + b)). Ky është vetëm një njoftim i vogël; në artikujt e mëposhtëm do t'ju ofroj menunë e plotë.

Digresion lirik: disa njerëz mendojnë diçka si kjo: "Hej, nuk është e përshtatshme të kesh një drejtim Veri/Lindje në vend të një këndi të thjeshtë që anija ta ndjekë!"

A është e vërtetë? Mirë, shiko dorën tënde të djathtë. Cili është këndi midis bazës së gishtit tuaj të vogël dhe majës së gishtit tuaj tregues? Fat i mirë me metodën tuaj të llogaritjes.

Ose thjesht mund të përgjigjeni, "Epo, maja është X inç në të djathtë dhe Y inç lart", dhe mund të bëni diçka për këtë.

A po afrohen numrat kompleksë?

Kemi kaluar nëpër zbulimet e mia bazë në fushën e numrave kompleksë si një tornado. Shikoni ilustrimin e parë, tani duhet të bëhet më e qartë.

Ka shumë më tepër për të zbuluar në këto numra të bukur, të mrekullueshëm, por truri im tashmë është i lodhur. Qëllimi im ishte i thjeshtë:

• Ju bindin se numrat kompleks shiheshin vetëm si "të çmendur", por në fakt ata mund të jenë shumë të dobishëm (ashtu si numrat negativë)
• Tregoni se si numrat kompleks mund të thjeshtojnë disa probleme si rrotullimi.

Nëse më duket tepër i shqetësuar për këtë temë, ka një arsye për këtë. Numrat imagjinarë kanë qenë një obsesion i imi prej vitesh - mungesa e të kuptuarit më acaroi.

Por ndezja e një qirije është më mirë sesa të kalosh nëpër errësirë ​​të madhe: këto janë mendimet e mia dhe jam i sigurt se drita do të ndizet në mendjet e lexuesve të mi.

Epilogu: Por ata janë ende shumë të çuditshëm!

E di që edhe mua më duken ende të çuditshëm. Po përpiqem të mendoj si personi i parë që zbuloi mendimin zero.

Zero është një ide kaq e çuditshme, "diçka" përfaqëson "asgjë" dhe kjo nuk mund të kuptohej në Romën e lashtë. Është e njëjta gjë me numrat kompleks - është një mënyrë e re e të menduarit. Por si numrat zero ashtu edhe ato komplekse e thjeshtojnë shumë matematikën. Nëse nuk do të kishim prezantuar kurrë gjëra të çuditshme si sistemet e reja të numrave, do të numëronim gjithçka në gishta.

E përsëris këtë analogji sepse është kaq e lehtë të fillosh të mendosh se numrat kompleksë "nuk janë normalë". Le të jemi të hapur ndaj inovacionit: në të ardhmen, njerëzit do të bëjnë vetëm shaka sesi dikush deri në shekullin e 21-të nuk besonte në numra komplekse.

Teksti pjesë e botimit

përmbajtja
Hyrje…………………………………………………………………………..3 Kapitulli I. Nga historia e numrave kompleks………………………………… ………………………… ............4 Kapitulli II. Bazat e metodës së numrit kompleks……………………………………6 Kapitulli III. Gjeometria e një trekëndëshi në numrat kompleks…………………….12 Kapitulli IV. Zgjidhja e problemeve të Provimit të Unifikuar të Shtetit dhe olimpiadave të ndryshme duke përdorur metodën e numrave kompleks………………………………………………………………………………………………………………………………………………………………………………………………………………………… Përfundim………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… ..25

Hyrje
Rëndësia e madhe e numrave kompleksë në matematikë dhe aplikimet e saj është e njohur gjerësisht. Algjebra e numrave kompleks mund të përdoret me sukses në gjeometrinë elementare, trigonometrinë, teorinë e lëvizjeve dhe ngjashmërive, si dhe në inxhinierinë elektrike, në probleme të ndryshme mekanike dhe fizike. Në planimetri, metoda e numrave kompleks ju lejon të zgjidhni problemet me llogaritje të drejtpërdrejta duke përdorur formula të gatshme. Kjo është thjeshtësia e kësaj metode, në krahasim me metodat vektoriale dhe koordinative, metodën e transformimeve gjeometrike, të cilat kërkojnë nga studentët të kenë inteligjencë të konsiderueshme dhe kërkime të gjata. Për disa mijëvjeçarë, trekëndëshi ka qenë një simbol i gjeometrisë. Madje mund të thuash se një trekëndësh është një atom gjeometrie. Çdo shumëkëndësh mund të ndahet në trekëndësha dhe studimi i vetive të tij zbret në studimin e vetive të trekëndëshave të përbërësve të tij. Le të shqyrtojmë se si funksionon metoda e numrave kompleksë kur vërtetohen vetitë e një trekëndëshi nga një kurs planimetrie shkollore, si dhe për zgjidhjen e problemeve C-4 të Provimit të Unifikuar të Shtetit. 2

Kapitulli I. Nga historia e numrave kompleks,
Për herë të parë, me sa duket, sasitë imagjinare u përmendën në veprën e famshme "Arti i madh, ose mbi rregullat e algjebrës" nga Cardano (1545), si pjesë e një zgjidhjeje formale për problemin e llogaritjes së dy numrave që mblidhen deri në 10 dhe kur shumëzohet jepni 40. Ai Për këtë problem, përftova një ekuacion kuadratik për një nga termat dhe gjeta rrënjët e tij: 5 + √ − 15 dhe 5 − √ − 15. Në një koment për zgjidhjen, ai shkroi: "këto sasi më komplekse janë të padobishme, megjithëse shumë gjeniale" dhe "Konsideratat aritmetike po bëhen gjithnjë e më të pakapshme, duke arritur një kufi sa delikate aq edhe të padobishme". Mundësia e përdorimit të madhësive imagjinare gjatë zgjidhjes së një ekuacioni kub, në të ashtuquajturën rast të pakalueshëm (kur rrënjët reale të një polinomi shprehen përmes rrënjëve kubike të madhësive imagjinare), u përshkrua për herë të parë nga Bombelli (1572). Ai ishte i pari që përshkroi rregullat e mbledhjes, zbritjes, shumëzimit dhe pjesëtimit të numrave kompleksë, por megjithatë i konsideroi ato një "shpikje" të padobishme dhe dinake. Shprehjet e përfaqësuara në formën a + b √ − 1, të shfaqura gjatë zgjidhjes së ekuacioneve kuadratike dhe kubike, filluan të quhen "imagjinare" në shekujt 16-17 me sugjerimin e Dekartit, i cili i quajti kështu, duke hedhur poshtë realitetin e tyre dhe për shumë të tjera të mëdha Për shkencëtarët e shekullit të 17-të, natyra dhe e drejta për ekzistencën e sasive imagjinare dukeshin shumë të dyshimta, ashtu si numrat irracionalë dhe madje edhe sasitë negative konsideroheshin të dyshimta në atë kohë. Përkundër kësaj, matematikanët zbatuan me guxim metodat formale të algjebrës së sasive reale në ato komplekse, morën rezultate të sakta reale edhe nga ato komplekse të ndërmjetme, dhe kjo nuk mund të mos fillonte të frymëzonte besim. Për një kohë të gjatë ishte e paqartë nëse të gjitha veprimet mbi numrat kompleks çojnë në rezultate komplekse ose reale, ose nëse, për shembull, nxjerrja e një rrënjë mund të çojë në zbulimin e disa llojeve të tjera të reja numrash. Problemi i shprehjes së rrënjëve të shkallës n nga një numër i caktuar u zgjidh në veprat e Moivre (1707) dhe Cotes (1722). Simboli për të treguar njësinë imagjinare u propozua nga Euler (1777, botuar 1794), i cili mori shkronjën e parë të fjalës latine për këtë. 3
Modeli aritmetik (standard) i numrave kompleks si çifte numrash realë u ndërtua nga Hamilton (1837); kjo vërtetoi qëndrueshmërinë e vetive të tyre. Shumë më herët, në vitin 1685, në veprën e tij "Algjebra", Wallis (Angli) tregoi se rrënjët komplekse të një ekuacioni kuadratik me koeficientë realë mund të përfaqësohen gjeometrikisht, me pika në rrafsh. Por kaloi pa u vënë re. Herën tjetër një interpretim gjeometrik i numrave kompleksë dhe veprimeve mbi to u shfaq në veprën e Wessel (1799). Përfaqësimi gjeometrik modern, i quajtur ndonjëherë "diagrami Argand", hyri në përdorim pas botimit të punës së J. R. Argand në 1806 dhe 1814, i cili përsëriti në mënyrë të pavarur përfundimet e Wessel. Termat "modul", "argument" dhe "numër i konjuguar" u prezantuan nga Cauchy. Kështu, u zbulua se numrat kompleksë janë gjithashtu të përshtatshëm për kryerjen e veprimeve thjesht algjebrike të mbledhjes, zbritjes, shumëzimit dhe ndarjes së vektorëve në rrafsh, gjë që ndryshoi shumë algjebrën vektoriale. 4

Kapitulli II. Bazat e metodës së numrit kompleks
[ 1 ]
,
[2], [3] [4] Interpretimi gjeometrik i numrave kompleksë Gjatësia e një segmenti Duke pasur parasysh një sistem koordinativ drejtkëndor kartezian në një rrafsh, numri kompleks z = x+iy (i 2 = -1) mund të jetë një me- njëra e lidhur me pikën M të rrafshit me koordinatat x, y (Fig. 1): z = x + iy ↔M (x, y) ↔M (z). Numri z quhet atëherë koordinata komplekse e pikës M. Meqenëse bashkësia e pikave të rrafshit Euklidian është në korrespondencë një me një me bashkësinë e numrave kompleksë, ky plan quhet edhe rrafshi i numrave kompleks. Origjina O e sistemit koordinativ kartezian quhet pika fillestare ose zero e rrafshit të numrave kompleks. Kur = 0 numri z është real. Numrat realë përfaqësohen me pika në boshtin x, për këtë arsye quhet bosht real. Në x=0, numri z është thjesht imagjinar: z=iy. Numrat imagjinarë përfaqësohen me pika në boshtin y, prandaj quhet bosht imagjinar. Zero është një numër real dhe thjesht imagjinar. Largësia nga fillimi i rrafshit O deri në pikën M(z) quhet modul i numrit kompleks z dhe shënohet me |z| ose r: | z | = r = | OM | = √ x 2 + y 2 Nëse φ është këndi i orientuar i formuar nga vektori ⃗ OM me boshtin x, atëherë sipas përcaktimit të funksionit sinus dhe kosinus sin φ = y r, cos φ = x r 5
prej nga x = r cos φ, y = r sin φ, dhe prandaj z = r (cos φ + sin φ). Ky paraqitje e një numri kompleks z quhet i tij
trigonometria

cheskoe
formë.
Paraqitja origjinale z=x+iy quhet
algjebrike
formën e këtij numri. Në paraqitjen trigonometrike, këndi  quhet argument i një numri kompleks dhe shënohet gjithashtu me arg z: φ = arg z Nëse jepet një numër kompleks z = x + iy, atëherë thirret numri ´ z = x − iy.
konjuguar kompleks
(ose thjesht
konjuguar
) në këtë numër z. Atëherë, padyshim, numri z është gjithashtu i konjuguar me numrin ´ z. Pikat M(z) dhe M 1 (´z) janë simetrike rreth boshtit x Nga barazia z = ´ z del se y = 0 dhe anasjelltas. Kjo do të thotë se

një numër i barabartë me
ndaj konjugatit të tij është real dhe anasjelltas.
Pikat me koordinata komplekse z dhe -z janë simetrike në lidhje me pikën fillestare O. Pikat me koordinata komplekse z dhe − ´ z janë simetrike në lidhje me boshtin y. Nga barazia z = ´ z del se x = 0 dhe anasjelltas. Prandaj, kushti z =− ´ z është një kriter për një numër thjesht imagjinar. Për çdo numër z, padyshim | z | = | ´ z | =¿− z ∨¿∨−´ z ∨¿ .
dy numra kompleksë të konjuguar janë numra realë: z + ´ z = 2 z, z ´ z = x 2 + y 2 =¿ z 2 ∨¿. Një numër i konjuguar me një shumë, produkt ose herës të kompleksit 6
numrat janë, respektivisht, shuma, prodhimi ose herësi i numrave të konjuguar me numrat e dhënë kompleks: ´ z 1 + z 2 = ´ z 1 + ´ z 2 ; ´ z 1 z 2 = ´ z 1 ´ z 2; ´ z 1: z 2 = ´ z 1: ´ z 2 Këto barazi mund të verifikohen lehtësisht duke përdorur formulat për veprimet mbi numrat kompleks. Nëse a dhe b janë koordinatat komplekse të pikave A dhe B, përkatësisht, atëherë numri c = a + b është koordinata e pikës C, e tillë që ⃗ OC = ⃗ OA + ⃗ OB (Fig. 3). Një numër kompleks d = a − b korrespondon me një pikë D të tillë që ⃗ OD = ⃗ OA − ⃗ OB. Distanca ndërmjet pikave A dhe B është | ⃗BA | = | ⃗ OD | =¿ a − b ∨¿: ¿ AB ∨¿∨ a − b ∨¿ (1) Meqenëse ¿ z ∨ 2 = z ´ z, atëherë ¿ AB ∨ 2 =(a − b) (´ a − ´ b) . (2)
Ekuacioni
z ´ z = r 2
përcakton një rreth me qendër

Rreth rrezes

r.
Lidhja AC CB = λ, (λ ≠ − 1), në të cilën pika C ndan një segment të caktuar AB, shprehet përmes koordinatave komplekse të këtyre pikave si më poshtë: λ = c − a b − c, λ = ´ λ, prej nga c = a + λb 1 + λ (3) Kur λ = 1, pika C është mesi i segmentit AB dhe anasjelltas. Atëherë: c = 1 2 (a + b) (4) Shumëzimi i numrave kompleks Shumëzimi i numrave kompleks kryhet sipas formulës, Dmth | a b | = | a || b | , dhe 7
Paralelizmi dhe pinguliteti Kolineariteti i tre pikave Le të jepen pikat A(a) dhe B(b) në rrafshin e numrave kompleksë. Vektorët ⃗ OA dhe ⃗ OB janë të bashkëdrejtuar nëse dhe vetëm nëse arg a = arg b, d.m.th. kur arg a – arg b=arg a b =0 (kur pjesëtohen numrat kompleks, argumenti i pjesëtuesit zbritet nga argumenti i divident).
Është gjithashtu e qartë se këta vektorë janë të drejtuar në drejtime të kundërta nëse dhe vetëm nëse arg a - arg b= arg a b = ± π. Numrat kompleks me argumentet 0, π, - π janë real.
Në mënyrë që pikat A(a) dhe B(b) të jenë kolineare me pikën fillestare O, është e nevojshme dhe e mjaftueshme që herësi a b të jetë një numër real, d.m.th. a b = ´ a ´ b ose a ´ b = ´ a b (6 ) Tani merrni pikat A(a), B(b), C(c), D(d). Vektorët ⃗ BA dhe ⃗ DC collie janë joar nëse dhe vetëm nëse pikat e përcaktuara nga numrat kompleks a-b dhe c-d janë në linjë me origjinën O. Vërejtje: 1. Bazuar në (6) kemi: ⃗ AB ∨¿ ⃗ CD↔ (a − b) (´ c − ´ d) =(´ a − ´ b) (c − d) ; (8) 2. Nëse pikat A, B, C, D i përkasin rrethit njësi z ´ z = 1, atëherë ´ a = 1 a; ´b = 1 b; ´c = 1 c; ´ d = 1 d dhe prandaj kushti (8) merr formën: ⃗ AB ∨¿ ⃗ CD↔ ab = cd ; (9) 3. Kolineariteti i pikave A, B, C karakterizohet nga kolineariteti i vektorëve ⃗AB dhe ⃗AC. Duke përdorur (8), marrim: (a − b) (´ a −´ c) =(´ a − ´ b) (a − c) (10) Ky është kriteri që pikat A, B, C t'i përkasin në të njëjtën vijë të drejtë. Mund të paraqitet në formën simetrike a (´ b −´ c) + b (´ c −´ a) + c (´ a − ´ b) = 0 (11) 8
Nëse pikat A dhe B i përkasin rrethit njësi z ´ z = 1, atëherë ´ a = 1 a; ´ b = 1 b dhe për këtë arsye secila nga relacionet (10) dhe (11) shndërrohet (pas reduktimit me (a-b) në sa vijon: c + ab ´ c = a + b (12) Pikat A dhe B janë të fiksuara, dhe pikën Ne do ta konsiderojmë C një variabël, duke ridizenjuar koordinatat e saj me z. z + (b − a) ´ z + a ´ b − b ´ a = 0 , (10a) z + ab ´ z = a + b (12a) Në veçanti, OA e drejtpërdrejtë ka ekuacionin a ´ z = ´ a z janë thjesht imagjinare Prandaj, OA ⊥ OB↔ a b = − ´ a ´ b ose OA ⊥ OB↔a ´ b + ´ a b = 0 (13) Perpendikulariteti i segmenteve AB dhe CD përcaktohet nga barazia (a. − b) (´ c − ´ d) + (´ a − ´ b) (c − d) = 0 (14) Në veçanti, kur pikat A, B, C, D i përkasin rrethit njësi z ´ z = 1 , atëherë thjeshtësohet varësia (14): ab + cd = 0 (15) Prodhimi skalar i vektorëve Le të shprehim prodhimin skalar të vektorëve ⃗ OA dhe ⃗ OB në terma të koordinatave komplekse a dhe b të pikave A dhe B. Le të a=x 1 +iy 1 , b=x 2 +iy 2 . Atëherë a b + a b=(x 1 +iy 1)(x 2 −iy 2)+(x 1 −iy 1)(x 2 +iy 2)=2(x 1 x 2 +y 1 y 2)= 2 ⃗ OA∙⃗OB. Pra, ⃗ OA ∙ ⃗ OB = 1 2 (a b + ab) (16) 9
Le të jepen tani katër pika arbitrare A(a), B(b), C(c), D(d) me koordinatat e tyre komplekse. Atëherë 2 ⃗ AB ∙ ⃗ CB = 1 2 (a-b)(c - d)+(a - b)(c-d) (17) Kënde Le të biem dakord të shënojmë me simbolin ∠ (AB ,CD) këndin e orientuar pozitivisht përmes të cilin vektori ⃗ duhet të rrotullohet AB në mënyrë që të bëhet në një linjë me vektorin ⃗ CD. Atëherë, cos ∠ (AB, CD)= (d − c) (´ b − ´ a) +(´ d −´ c)(b − a) 2 | d − c || b − a |
(18) sin ∠ (AB ,CD)= (d − c) (´ b −´ a) +(´ d −´ c)(b − a) 2 i | d − c || b − a |
(19) Pika e kryqëzimit të sekanteve në një rreth Nëse pikat A, B, C dhe D shtrihen në rrethin z ´ z = 1, atëherë koordinata komplekse e pikës së kryqëzimit gjendet me formulën ´ z = (a + b) − (c + d) ab − cd (20) Nëse AB është pingul me CD, atëherë z= 1 2 (a+b+c+d) (21) Pika e prerjes së tangjenteve në rrethin 10

Koordinata komplekse e pikës së prerjes së tangjenteve në rrethin z ´ z =1 në pikat e tij A(a) dhe B(b) gjendet me formulën z= 2ab a + b (22) Projeksioni ortogonal i një pike. mbi një drejtëz Projeksion ortogonal i një pike M(m) në një drejtëz AB, ku A(a) dhe B(b) gjendet me formulën Në rastin kur A dhe B i përkasin rrethit njësi z= 1 2 (a + b + m − cb m) .
Kapitulli III.
Nga vjen h=a+b+c. (24) Shprehja që rezulton përfshin koordinatat e kulmeve të trekëndëshit në mënyrë simetrike, prandaj lartësia e tretë e trekëndëshit kalon nëpër pikën e kryqëzimit të dy trekëndëshave të parë [2,1] Trekëndëshat ABC dhe A 1 B 1 C 1 janë të ngjashme dhe të orientuara në mënyrë identike (ngjashmëria e llojit të parë), nëse B 1 =kAB, A 1 B 1 =kAC dhe këndet B 1 A 1 C 1 dhe BAC janë të barabarta (këndet janë të orientuara). Duke përdorur numrat kompleks, këto barazi mund të shkruhen si më poshtë: |a 1 −b 1 |=k|a−b|, |a 1 −c 1 |=k|a−c|,arg c 1 − a 1 b 1 − a 1 =arg c − a b − a . Dy barazitë janë ekuivalente me një me 1 − a 1 c − a = b 1 − a 1 b − a = σ , (25) ku σ është një numër kompleks, |σ|=k-koeficienti i ngjashmërisë. Nëse σ është real, atëherë c 1 − a 1 c − a = ´ c 1 − ´ a 1 ´ c − ´ a , ku AC║A 1 C 1. Rrjedhimisht, trekëndëshat ABC dhe A 1 B 1 C 1 janë homotetikë. Lidhja (25) është kusht i domosdoshëm dhe i mjaftueshëm që trekëndëshat ABC dhe A 1 B 1 C 1 të jenë të ngjashëm dhe të orientuar njësoj. Mund t'i jepet një trajtë simetrike ab 1 +bc 1 +ca 1 =ba 1 +cb 1 +ac 1 (25a) Trekëndësha të barabartë Nëse | σ | = 1, atëherë trekëndëshat ABC dhe A 1 B 1 C 1 janë të barabartë. Atëherë lidhja (25) është një shenjë e barazisë së trekëndëshave të orientuar në mënyrë identike, dhe relacioni (26) është një shenjë e barazisë së trekëndëshave të orientuar në mënyrë të kundërt. Trekëndëshat e rregullt Nëse kërkojmë që trekëndëshi i orientuar ABC të jetë i ngjashëm me trekëndëshin e orientuar BCA, atëherë trekëndëshi ABC do të jetë i rregullt. 12
Prandaj, nga (25) marrim një kusht të domosdoshëm dhe të mjaftueshëm që trekëndëshi ABC të jetë i rregullt (a−b) 2 +(b−c) 2 +(c−a) 2 =0 (27) Sipërfaqja e trekëndëshit (vërtetuar nga autori) Ne nxjerrim formulën për zonën S të një trekëndëshi të orientuar pozitivisht ABC: S = 1 2 | AB || AC | sin ∠ (AB , AC)= 1 4i ((c − a) (´ b − ´ a) − (b − a) (´ c − ´ a)) = − 1 4i (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b)) ose S = i 4 (a (´ b − ´ c) + b (´ c − ´ a) + c (´ a − ´ b )) (28) Nëse trekëndëshi ABC është i brendashkruar në një rreth z ´ z = 1, atëherë formula (28) shndërrohet në formën: S = i 4 (a − b) (b − c) (c − a) abc (29) Teorema për mesin e një trekëndëshi (e vërtetuar nga autori)
Teorema
. Vija e mesme e trekëndëshit është paralele me bazën dhe e barabartë me gjysmën e saj. Dëshmi. Le të jenë pikat M dhe N pikat e mesit të brinjëve AB dhe BC, atëherë m = b 2 ; n = b + c 2 . Meqenëse z 2 =z ´ z, atëherë MN 2 =(m-n)(´ m - ´ n)=(b 2 - b + c 2) (´ b 2 – ´ b + ´ c 2)= b ´ b 4 − b ´ b + b ´ c 4 − b ´ b + ´ b c 4 + b ´ b + b ´ c + ´ b c + c ´ c 4 = c ´ c 4 13
4MN 2 =c ´ c, AC 2 =(c-0)(c-0)=c´ c, prandaj 4MN 2 = AC 2 ose 2MN=AC është plotësuar edhe gjendja (8) e kolinearitetit të vektorëve MN dhe AC , dhe për këtë arsye MN ║AC. Teorema e Talesit (e vërtetuar nga autori)
Teorema
. Nëse në njërën anë të një këndi vijat paralele presin segmente të barabarta, atëherë në anën tjetër të këndit ato presin segmente të barabarta. Vërtetim Le të supozojmë se c=kb. Atëherë nëse BD||CE, atëherë kemi (b-d)(´ c − 2 ´ d ¿= (´ b − ´ d) (c − 2d) Duke hapur kllapat dhe duke sjellë terma të ngjashëm, marrim ekuacionin b ´ c − 2 b ´ d −´ c d = ´ b c − 2 ´ b d − c ´ d Duke zëvendësuar c me kb dhe ´ c me k ´ b, marrim bk ´ b -2b ´ d -dk ´ b = ´ b kb-2 ´ b d-kb ´ d Duke sjellë përsëri terma të ngjashëm dhe duke lëvizur gjithçka në njërën anë, marrim 2b ´ d + dk ´ b − 2 ´ b d − kb ´ d =0 ´ d − ´ b d ¿+ k ( ´ b d − b ´ d) = 0. Prandaj k=2, d.m.th. c=2b, në mënyrë të ngjashme, vërtetohet se f=3b, etj. Teorema e Pitagorës (e vërtetuar nga autori). një trekëndësh kënddrejtë, katrori i hipotenuzës është i barabartë me shumën e katrorëve të këmbëve 14
Dëshmi. Distanca ndërmjet pikave B dhe C është e barabartë me BC=|b-c|=b, BC 2 =b ´ b. Që nga |z| 2 = z ´ z , pastaj AC 2 =(a-c)(c ´ a − ´ ¿ ¿=(a − 0) (´ a - 0)=a ´ a . AB 2 =(a-b)(´ a − ´ b ¿= a ´ a − a ´ b - ´ a b+b ´ b Meqenëse b është një numër real, d.m.th. b= ´ b , atëherë -a ´ b =− ab në boshtin Oy a, që është - 'ab = ab Kështu, AB 2 = a 'a -a ´ b - ´ ab +b ´ b = a ´ a +b ´ b = AC 2 + BC 2. Teorema është e vërtetuar drejtëz (e vërtetuar nga autori) Le të vërtetojmë se qendra, qendra dhe rrethi i trekëndëshit shtrihen në të njëjtën drejtëz (kjo drejtëz quhet drejtëza e Euler-it), dhe OG = 1/2GH 15.
Vërtetim: Pika G(g) është qendra e trekëndëshit ABC, H(h) është ortoqendra dhe O(o) është qendra e rrethit të rrethuar të trekëndëshit. Në mënyrë që këto pika të jenë kolineare, duhet të plotësohet barazia (10): (g-o)(´ g - ´ h ¿ -(´ g − ´ o ¿ (g − h) =0 Le të marrim pikën O si origjina, pastaj g(´g - ´ h ¿ - ´ g (g − h) =g 2 -g ´ h −¿ (g 2 - h ´ g ¿ =-g ´ h + h ´ g (30) koordinata komplekse e ortoqendrës llogaritet sipas formulës (24) h=a+b+c, (30a) dhe centroidi sipas formulës (23) g = 1 3 (a + b + c) (30c) Zëvendësohet në ( 30), marrim 1 3 (a+b +c)(´ a + b + c)-(a+b+c)(´ a + b + c 1 3 ¿))=0 të kënaqur, pra, qendra, ortoqendra dhe qendra e trekëndëshit të rrethuar shtrihen në të njëjtën drejtëz OG=g= 1 3 (a+b+c) GH=h-g=a+b+c- 1 3 (a. +b+c)= 2 3 (a+b+c) Kuptuam se OG= 1 2 GH është vërtetuar 16.
Rrethi i Euler-it (rrethi me nëntë pika). Vërtetuar nga autori Konsideroni trekëndëshin ABC. Le të biem dakord që‌ | OA |
= | OB |
= | OC | =1, d.m.th. të gjitha kulmet e trekëndëshit i përkasin rrethit njësi z ´ z = 1 (qendra e rrethit rrethor O është origjina, dhe rrezja është njësia e gjatësisë). Le të vërtetojmë se bazat e tre lartësive të një trekëndëshi arbitrar, mesi i tre brinjëve të tij dhe mesi i tre segmenteve që lidhin kulmet e tij me qendrën ortoqendër shtrihen në të njëjtin rreth, dhe qendra e tij është mesi i segmentit OH. , ku H, kujtojmë, është ortoqendra e trekëndëshit ABC. Një rreth i tillë quhet
Sepse trekëndëshi ABC është brendashkruar në rrethin z ´ z = 1, pastaj | a | = | b | = | c | = 1,→ | a 2 | = | b 2 | = | c 2 | = 1 2 | a || b | | c | = 1 2 | a || c | | b | = 1 2 | b || c | | a | = 1 2 Pra, pikat D, E, F, K, L, M, N, Q, F i përkasin të njëjtit rreth teorema e Gausit Nëse një drejtëz i pret drejtëzat që përmbajnë brinjët BC, CA, AB të trekëndëshit ABC, përkatësisht në pikat A 1, B 1 , C 1, pastaj pikat e mesme të segmenteve AA 1, BB 1, СС 1 janë kolineare. Duke përdorur (11), shkruajmë kushtet për kolinearitetin e trinjakëve të pikave AB 1 C, CA 1 B, BC 1 A, A 1 B 1 C 1: 0,) b - a (c) a - c () c - b (a 0 ,) c - b a() b - a () a - c b(0,) a - c b() c - b () b - a c(0,) b - a (c) a - c () c - b a (1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1             b c a b, janë pika P, (3) segmentet AA 1, BB 1, CC 1 , atëherë duhet të tregojmë se 0) () () (      n m p m p n p n m (32) Meqenëse), (2 1), (2 1), (2 1 1 1 1 c c p b b n a m       atëherë barazia që vërtetohet (31) është ekuivalente me këtë: 0))(())())(1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1              b a a c c a c c b b c c b b a a ose pas shumëzimit: 0) () () () () () () () () () () () () (1 1 11 1 1 1 1 1 1 1 1 1 1 1 1                           b a me b a c b a c a c b a me b a c b a c b c b a c b a c b a c a (33) Tani është e lehtë të shihet se ( 33) fitohet me mbledhje termike të barazive (31).

Kapitulli IV.

Zgjidhja e problemeve të USE dhe olimpiadave të ndryshme duke përdorur metodën e numrave kompleks.
Problemi 1. Provimi i Unifikuar i Shtetit -2012, P-4 Në një vijë që përmban medianën AD të një trekëndëshi kënddrejtë ABC me kënd të drejtë C, merret një pikë E, e largët nga kulmi A në një distancë të barabartë me 4. Gjeni sipërfaqen e trekëndëshi BCE nëse BC=6, AC=4. Zgjidhja e parë. Sipas teoremës së Pitagorës AD=5. Atëherë ED=1 Le të shtrihet pika E në rreze AD. Medianaja AD është më e gjatë se AE, dhe pika E shtrihet brenda trekëndëshit ABC (Fig. 1) Le të hedhim EF pingul nga pika E në drejtëzën BC dhe të marrim parasysh trekëndëshat e ngjashëm me kënd të drejtë DEF dhe DAC. Nga ngjashmëria e këtyre trekëndëshave gjejmë: EF = AC ∙ ED AD = 4 5 19
Prandaj, S pes = 1 2 ∙ 6 ∙ 4 5 = 2.4. Tani le të shtrihet pika A midis E dhe D (Fig. 2). Në këtë rast ED=9 dhe EF = AC ∙ ED AD = 36 5 . Atëherë S BCE = 1 2 ∙ 6 ∙ 36 5 = 21,6. Përgjigje: 2.4; 21.6. Zgjidhja e problemit duke përdorur numra kompleks. Rasti I: pika E shtrihet në rreze AD. Meqenëse D është mesi i CB, atëherë CD=3. Dhe meqenëse CA=4, është e qartë se AD=5, d.m.th. DE=1. Le të marrim pikën C si pikë fillestare, dhe linjat CA dhe CB si boshtet reale dhe imagjinare. Pastaj A(4), C(0), B(6i), D(3i), E(e). Pikat A, E dhe D janë kolineare, atëherë e − 4 3i − e = 4 dmth e= 12i + 4 5 . Sipas formulës (25) S CBE =│ ´ i 4 (e6 ´ i +6i(− ´ e)│= e e − ´ ¿ 6 i 2 4 ¿ ¿ =2.4 Rasti II: pika A shtrihet ndërmjet pikave D dhe E , atëherë 4 − e 3i − 4 = 4 5 , pra e= 36 − 12 i 5 S CBE = 3 i 2 2 (36 − 12 i 5 − − 36 − 12i 5) : 2.4 dhe 21.6 | Mënyra e parë, ju duhet të keni një numër supozimesh, të cilat mund të mos shfaqen menjëherë, por pas një periudhe mjaft të gjatë arsyetimi, megjithëse, nëse studenti është i përgatitur mirë, atëherë vetë zgjidhja formohet në çast Mënyra e dytë, ne përdorim formula të gatshme, duke kursyer kohë në kërkim, megjithatë, ne e kuptojmë se pa njohur formulat, problemet nuk mund të zgjidhen duke përdorur metodën e numrave kompleks .
Detyra 2 (MIOO, 2011):
“Pika M shtrihet në segmentin AB. Në një rreth me diametër AB, merret pika C, e largët nga pikat A, M dhe B në distancë përkatësisht 20, 14 dhe 15. Gjeni zonën e trekëndëshit BMC." 20
Zgjidhje: Meqenëse AB është diametri i një rrethi, atëherë ∆ ABC është drejtkëndëshe, ∠ C = 90 ° Le të marrim C si pikë zero të rrafshit, pastaj A(20i), B(15), M(z). Meqenëse CM=14, barazia z ´ z = 196 është e vlefshme, pra pika M ∈ një rreth me qendër në pikën C dhe r=14. Le të gjejmë pikat e kryqëzimit të këtij rrethi me drejtëzën AB: Ekuacioni i drejtëzës AB (10a): 20 i (15 −´ z) + 15 (´ z + 20 i) + z (− 20 i − 15) = 0 Duke zëvendësuar ´ z me 196 z dhe duke shumëzuar të gjithë ekuacionin me (4 i − 3) , marrim një ekuacion kuadratik për z: 25 z 2 + 120 i (4 i − 3) z + 196 (4 i − 3) 2 = 0 z 1,2 = 2 (3 − 4 i) (6 i± √ 13) 5 Duke përdorur formulën (28), gjejmë zonën ∆ MBC: S = i 4 (z (´ b − ´ c) + b (´ c − ´ z) + c (´ z − ´ b)) Ku c = 0, ´ c = 0, b = 15, ´ b = 15, ´ z = 196 ∗ 5 2 (3 − 4 i) (6 i ± √ 13) Pasi kemi kryer transformime ekuivalente, marrim S = 54 ± 12 √ 13 sq. njësi Përgjigju. 54 ± 12 √ 13 sq. njësi Nëse e zgjidhni problemin duke përdorur metoda gjeometrike, atëherë duhet të merrni parasysh dy raste të ndryshme: 1- pika M shtrihet midis A dhe D; 2 - midis D dhe B. 21

Kur zgjidhni një problem duke përdorur metodën e numrave kompleksë, dualiteti i zgjidhjes fitohet për shkak të pranisë së dy pikave të kryqëzimit të një rrethi dhe një drejtëze. Kjo rrethanë na lejon të shmangim një gabim të zakonshëm.
Problemi 3
Medianat AA 1, BB 1 dhe CC 1 të trekëndëshit ABC priten në pikën M. Dihet se AB=6MC 1. Vërtetoni se trekëndëshi ABC është trekëndësh kënddrejtë. Zgjidhje: Le të jetë C pika zero e rrafshit dhe cakto një njësi reale pikës A. Më pas problemi reduktohet në vërtetimin se b është një numër thjesht imagjinar. AB 2 = (b − 1) (´ b − 1) . M është qendra, koordinata e tij është 1 3 b + 1 3 MC 1 2 = (1 3 b + 1 3 − 1 2 b − 1 2) (1 3 ´ b + 1 3 − 1 2 ´ b − 1 2) = 1 3 b (b + 1) (´ b + 1) Meqenëse AB=6MC 1, atëherë (b − 1) (´ b − 1) = (b + 1) (´ b + 1) . Pasi kemi kryer transformimet, marrim b =− ´ b, pra b është një numër thjesht imagjinar, pra këndi C është një drejtëz.
Detyra 4.
22
Si rezultat i një rrotullimi 90° rreth pikës O, segmenti AB u shndërrua në segmentin A "B". Vërtetoni se medianaja OM e trekëndëshit OAB " është pingul me drejtëzën A " B . Zgjidhje: Le të jenë koordinatat O, A, B përkatësisht 0,1, b. Atëherë pikat A " dhe B " do të kenë koordinata a" = i dhe b" = bi, dhe mesi M i segmentit AB " do të ketë koordinata m = 1 2 (1 + bi). Gjejmë: a " − b m − 0 = i − b 1 2 (1 + bi) = 2 i (i − b) i − b = 2i numri është thjesht imagjinar. Bazuar në kriterin e pingulitetit (segmentet AB dhe CD janë pingul nëse dhe vetëm nëse numri a - b c - d është thjesht imagjinar), drejtëzat OM dhe A' B janë pingul.
Problemi 5
. 23
Nga baza e lartësisë së trekëndëshit, pingulet hidhen në dy anë që nuk korrespondojnë me këtë lartësi. Vërtetoni se distanca ndërmjet bazave të këtyre pingulave nuk varet nga zgjedhja e lartësisë së trekëndëshit. Zgjidhje: Le të jepet trekëndëshi ABC dhe rrethi i rrethuar rreth tij ka ekuacionin z ´ z = 1. Nëse CD është lartësia e trekëndëshit, atëherë d = 1 2 (a + b + c − ab c) Koordinatat komplekse të bazave M dhe N të pingulëve të rënë nga pika D në AC dhe BC, përkatësisht, janë të barabarta me m = 1 2 (a + c + d − ac ´ d 2) n = 1 2 (b + c + d − bc ´ d 2) Gjejmë: m − n = 1 2 (a − b + c ´ d ( b − a)) = 1 2 ( a − b) (1 − c ´ d) = (a − b) (a − c) (b − c) 4 ab Meqenëse | a | = | b | = 1, atëherë | m − n | = | (a − b) × (b − c) (c − a) | 4. Kjo shprehje është simetrike në lidhje me a, b, c, d.m.th. distanca MN nuk varet nga zgjedhja e lartësisë së trekëndëshit.
konkluzioni
24
"Sigurisht! Të gjitha problemet mund të zgjidhen pa numra kompleksë. Por fakti është se algjebra e numrave kompleks është një metodë tjetër efektive për zgjidhjen e problemeve planimetrike. Mund të flasim vetëm për zgjedhjen e një metode që është më efektive për një detyrë të caktuar. Mosmarrëveshjet në lidhje me avantazhet e një metode të veçantë janë të kota nëse i konsiderojmë këto metoda në përgjithësi, pa aplikim në një problem specifik” [2]. Një vend të madh në studimin e metodës zënë një sërë formulash. Kjo është
disavantazhi kryesor
metodë dhe në të njëjtën kohë
dinjitet
, pasi ju lejon të zgjidhni probleme mjaft komplekse duke përdorur formula të gatshme me llogaritjet elementare. Për më tepër, unë besoj se kjo metodë është universale kur zgjidhen problemet e planimetrisë.
Bibliografia
1. Markushevich A.I. Numrat kompleksë dhe pasqyrat konformale - M.: Shtëpia Botuese Shtetërore e Letërsisë Teknike dhe Teorike, 1954. - 52 f. 25
2. Ponarin Ya. 3. Shvetsov D. Nga linja e Simsonit te teorema Droz-Farney, Kvant. - Nr.6, 2009. – f. 44-48 4. Yaglom I. M. Shndërrime gjeometrike. Shndërrimet lineare dhe rrethore. - Shtëpia Botuese Shtetërore e Letërsisë Teknike-Teorike, 1956. – 612 f. 5. Yaglom I.M Numrat kompleks dhe zbatimi i tyre në gjeometri - M.: Fizmatgiz, 1963. - 192 f. 6. Morkovich A.G. dhe të tjera, Algjebra dhe fillimet e analizës matematikore të klasës së 10-të. Në 2 orë Pjesa 1. Libër mësuesi për studentët e institucioneve të arsimit të përgjithshëm (niveli i profilit) - M.: Mnemosyne, 2012. - 343 f. 7. Andronov I.K. Matematika e numrave realë dhe kompleksë - M.: Prosveshchenie, 1975. - 158 f. 26

Aplikimi

Teoremat klasike të gjeometrisë elementare

Teorema e Njutonit.
Në një katërkëndësh të rrethuar rreth një rrethi, pikat e mesit të diagonaleve janë në linjë me qendrën e rrethit. 27
Dëshmi. Le të marrim qendrën e rrethit si origjinë, duke vendosur rrezen e tij të barabartë me një. Le t'i shënojmë pikat e kontaktit të brinjëve të këtij trekëndëshi katërkëndësh A o B o C o D o me A, B, C, D (në mënyrë rrethore) (Fig. 4). Le të jenë M dhe N mesi i diagonaleve A o C o dhe B o D o, përkatësisht. Atëherë, sipas formulës për pikat e prerjes së tangjenteve në rrethin z = 2ab a + b, pikat A o , B o , C o , D o do të kenë koordinata komplekse, përkatësisht: , 2 , 2 , 2 , 2 0 0 0 0 d c cd d c b bc c b a ab b d a ad a         ku a, b, c, d janë koordinatat komplekse të pikave A, B, C, D. Prandaj.) (2 1 ,) (2 1 0 0 0 0 d c cd b a ab d b n c b bc d a ad c a m             Llogaritni m        b   Meqenëse, 1 , 1 b b a a   , 1 , 1 d d c c   atëherë drejtpërdrejt është e qartë se n m n m  Bazuar në (6), pikat O, M, N janë kolineare.
Teorema e Paskalit

.
Pikat e kryqëzimit të vijave që përmbajnë anët e kundërta të një gjashtëkëndëshi të brendashkruar shtrihen në të njëjtën vijë. 28
Dëshmi. Le të jenë të brendashkruar në një rreth gjashtëkëndëshi ABCDEF dhe P FA CD N EF BC M DE AB   ) () (,) () (,) () (   (Fig. 6) (Fig. 6). Le të marrim qendrën e rrethit si pikë zero të rrafshit, dhe rrezja e tij është për njësi gjatësie. Pastaj, sipas (17), kemi: ,) (,) (,) (fa cd a f d c p ef bc f e c b n. de ab e d b a m                Llogarit)     dhe në mënyrë të ngjashme .))(())((fa cd ef bc bc ab fa ef de cd f c p n           Më pas gjejmë: .))(())(de ab c f fa cd e m p n       Meqenëse numrat f e d c b a janë të barabartë, përkatësisht, f e d c b a 1 , 1 , 1 , 1, 1, 1, atëherë një kontroll me gojë zbulon se shprehja e gjetur përkon me konjugatin e saj, d.m.th. Kjo do të thotë se pikat M, N, P janë kolineare.
Teorema e Monges.
Në një katërkëndësh të gdhendur në një rreth, vijat që kalojnë nëpër mes pikat e anëve dhe. Çdo diagonale është pingul me anët e kundërta dhe, në përputhje me rrethanat, diagonalja tjetër kryqëzohet në një pikë. Quhet pika Monge e një katërkëndëshi ciklik. Dëshmi. Përgjysmuesit pingul me brinjët e katërkëndëshit ABCD kryqëzohen në qendër të rrethit, të cilin e marrim si pikënisje. Për çdo pikë M(z) të përgjysmuesit pingul me [AB] numri b a b a z   ) (2 1 thjesht imagjinar. 29
Në veçanti, për z=0 është e barabartë me) (2) (b a b a    Për çdo pikë N(z) të drejtëzës që kalon nga mesi i anës CD pingul me (AB), numri b a d c z   ) (2 1 do të duhet të jetë thjesht imagjinare dhe anasjelltas. Por për z=) (2 1 d c b a    është e barabartë) (2 b a b a   d.m.th. thjesht imagjinare. Prandaj, pika E me një koordinatë komplekse) ( 2 1 d c b a    shtrihet në vijën e treguar Dhe kjo shprehje është simetrike në lidhje me shkronjat a, b, c, d Prandaj, pesë rreshtat e tjerë të ndërtuar në mënyrë të ngjashme përmbajnë pikën E. 30

MUNDËSIA E PËRDORIMIT TË NUMRAVE KOMPLEKS

NË KURSIN E MATEMATIKËS NË SHKOLLA E ARSIMIT TË PËRGJITHSHËM

Drejtues shkencor:

Institucion arsimor komunal

Shkolla e mesme Pervomaiskaya

Me. Qyteti Kichmengsky

St. Zarechnaya 38

Puna e paraqitur i kushtohet studimit të numrave kompleks. Rëndësia: Zgjidhja e shumë problemeve në fizikë dhe teknologji çon në ekuacione kuadratike me një diskriminues negativ. Këto ekuacione nuk kanë zgjidhje në fushën e numrave realë. Por zgjidhja e shumë problemeve të tilla ka një kuptim fizik shumë të caktuar.

Rëndësia praktike: numrat kompleksë dhe funksionet e ndryshoreve komplekse përdoren në shumë çështje të shkencës dhe teknologjisë dhe mund të përdoren në shkollë për të zgjidhur ekuacionet kuadratike.

Zona e objektit: matematikë. Objekti i kërkimit: konceptet dhe veprimet algjebrike. Lënda e hulumtimit- numrat kompleks. Problem: numrat kompleks nuk studiohen në lëndën e matematikës në shkollën e mesme, megjithëse mund të përdoren për zgjidhjen e ekuacioneve kuadratike. Nuk mund të përjashtohet mundësia e futjes së numrave kompleksë në detyrat USE në të ardhmen. Hipoteza: Ju mund të përdorni numra kompleks për të zgjidhur ekuacionet kuadratike në shkollën e mesme. Synimi: të studiojë mundësinë e përdorimit të numrave kompleksë gjatë studimit të matematikës në klasën e 10-të të një shkolle të mesme. Detyrat: 1. Studioni teorinë e numrave kompleksë 2. Shqyrtoni mundësinë e përdorimit të numrave kompleks në një kurs matematike të klasës së 10-të. 3. Zhvilloni dhe testoni detyra me numra kompleks.

Numrat realë nuk mjaftojnë për të zgjidhur ekuacionet algjebrike. Prandaj, është e natyrshme të përpiqemi për t'i bërë këto ekuacione të zgjidhshme, gjë që çon në një zgjerim të konceptit të numrit..gif" width="10" height="65 src=">

https://pandia.ru/text/78/027/images/image005_18.gif" width="10" height="62">.gif" width="97" height="28 src=">

ju vetëm duhet të pranoni të veproni në shprehje të tilla sipas rregullave të algjebrës së zakonshme dhe të supozoni se

Në vitin 1572, u botua një libër i algjebristit italian R. Bombelli, në të cilin u vendosën rregullat e para për veprimet aritmetike mbi numra të tillë, deri në nxjerrjen e rrënjëve të kubit prej tyre. Emri "numrat imagjinarë" u prezantua në 1637. Matematikani dhe filozofi francez R. Descartes, dhe në 1777 një nga matematikanët më të mëdhenj të shekullit të 8-të X..gif" width="58" height="19"> si shembull i përdorimit të numrave kompleksë në studimin e matematikës. Në klasën e 10-të, numri x, katrori i të cilit është –1, quhet njësi imagjinare, pra ..gif" height="27 src=">.gif". width="100" height="27 src" =">klasa e 8-të" href="/text/category/8_klass/" rel="bookmark">klasa e 8-të në algjebër.- M.: Edukimi, 1994.-P. 134-139.

2. Fjalor Enciklopedik i një Matematikani të Ri / Përmbledhje. E-68. - M.: Pedagogji, 19s