Si të zgjidhim shprehjet me modul. Sa është moduli i një numri në matematikë
Shkolla e mesme MBOU nr. 17, Ivanovo
« Ekuacionet me modul"
Zhvillimi metodologjik
Përpiluar
mësues matematike
Lebedeva N.V.20010
Shënim shpjegues
Kapitulli 1. Hyrje
Seksioni 2. Vetitë themelore Seksioni 3. Interpretimi gjeometrik i konceptit të modulit të një numri Seksioni 4. Grafiku i funksionit y = |x| Seksioni 5. KonventatKapitulli 2. Zgjidhja e ekuacioneve që përmbajnë një modul
Seksioni 1. Ekuacionet e formës |F(x)| = m (më e thjeshta) Seksioni 2. Ekuacionet e formës F(|x|) = m Seksioni 3. Ekuacionet e formës |F(x)| = G(x) Seksioni 4. Ekuacionet e formës |F(x)| = ± F(x) (më e bukura) Seksioni 5. Ekuacionet e formës |F(x)| = |G(x)| Seksioni 6. Shembuj të zgjidhjes së ekuacioneve jo standarde Seksioni 7. Ekuacionet e formës |F(x)| + |G(x)| = 0 Seksioni 8. Ekuacionet e formës |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± në n | = m Seksioni 9. Ekuacionet që përmbajnë disa moduleKapitulli 3. Shembuj të zgjidhjes së ekuacioneve të ndryshme me modul.
Seksioni 1. Ekuacionet trigonometrike Seksioni 2. Ekuacionet eksponenciale Seksioni 3. Ekuacionet logaritmike Seksioni 4. Ekuacionet irracionale Seksioni 5. Detyrat e avancuara Përgjigjet e ushtrimeve ReferencatShënim shpjegues.
Koncepti i vlerës absolute (modulit) të një numri real është një nga karakteristikat thelbësore të tij. Ky koncept është i përhapur në seksione të ndryshme të shkencave fizike, matematikore dhe teknike. Në praktikën e mësimdhënies së kurseve të matematikës në shkollat e mesme në përputhje me Programin e Ministrisë së Mbrojtjes së Federatës Ruse, koncepti i "vlerës absolute të një numri" haset në mënyrë të përsëritur: në klasën e 6-të, përkufizimi i një moduli dhe futet kuptimi gjeometrik i tij; në klasën e 8-të formohet koncepti i gabimit absolut, merret parasysh zgjidhja e ekuacioneve dhe pabarazive më të thjeshta që përmbajnë një modul dhe studiohen vetitë e rrënjës katrore aritmetike; në klasën e 11-të koncepti gjendet në rubrikën “Rrënja n-shkalla e saj." Përvoja e mësimdhënies tregon se nxënësit shpesh hasin në vështirësi në zgjidhjen e detyrave që kërkojnë njohuri të këtij materiali dhe shpeshherë i anashkalojnë ato pa filluar t'i kryejnë. Tekstet e detyrave të provimit për lëndët e klasave të 9-ta dhe të 11-ta përfshijnë edhe detyra të ngjashme. Për më tepër, kërkesat që universitetet u vendosin maturantëve janë të ndryshme, përkatësisht në një nivel më të lartë se kërkesat e kurrikulës shkollore.Për jetën në shoqërinë moderne, formimi i një stili matematikor të të menduarit, i manifestuar në aftësi të caktuara mendore, është shumë i rëndësishëm. Në procesin e zgjidhjes së problemeve me module, kërkohet aftësia për të përdorur teknika të tilla si përgjithësimi dhe specifikimi, analiza, klasifikimi dhe sistemimi dhe analogjia. Zgjidhja e detyrave të tilla ju lejon të testoni njohuritë tuaja për seksionet kryesore të kursit shkollor, nivelin e të menduarit logjik dhe aftësitë fillestare të kërkimit.
Kjo punë i kushtohet njërit prej seksioneve - zgjidhja e ekuacioneve që përmban një modul. Ai përbëhet nga tre kapituj. Kapitulli i parë prezanton konceptet bazë dhe konsideratat më të rëndësishme teorike. Kapitulli i dytë propozon nëntë lloje kryesore të ekuacioneve që përmbajnë një modul, diskuton metodat për zgjidhjen e tyre dhe shqyrton shembuj të niveleve të ndryshme të kompleksitetit. Kapitulli i tretë ofron ekuacione më komplekse dhe jo standarde (trigonometrike, eksponenciale, logaritmike dhe irracionale). Për çdo lloj ekuacioni ka ushtrime për zgjidhje në mënyrë të pavarur (bashkangjitur përgjigjet dhe udhëzimet). .
Qëllimi kryesor i kësaj pune është të ofrojë ndihmë metodologjike për mësuesit në përgatitjen e mësimeve dhe në organizimin e lëndëve me zgjedhje. Materiali mund të përdoret edhe si mjet mësimor për nxënësit e shkollave të mesme. Detyrat e propozuara në vepër janë interesante dhe jo gjithmonë të lehta për t'u zgjidhur, gjë që bën të mundur që të bëhet më i ndërgjegjshëm motivimi arsimor i studentëve, të testohen aftësitë e tyre dhe të rritet niveli i përgatitjes së maturantëve për hyrjen në universitete. Një përzgjedhje e diferencuar e ushtrimeve të propozuara përfshin një kalim nga niveli riprodhues i zotërimit të materialit në atë krijues, si dhe mundësinë për të mësuar se si të zbatoni njohuritë tuaja kur zgjidhni probleme jo standarde. : Kapitulli 1. Hyrje. Seksioni 1. Përcaktimi i vlerës absolute Përkufizimi Seksioni 1. Përcaktimi i vlerës absolute Vlera absolute (moduli) e një numri real A një numër jo negativ quhet: │ Seksioni 1. Përcaktimi i vlerës absolute │ ose│ -A.
│a│ = │ 0, nëse a = 0 (1)
│ - dhe, nëse aShembuj: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- Zgjero modulin e shprehjes:
Seksioni 2. Vetitë themelore.
Le të shqyrtojmë vetitë themelore të vlerës absolute. Prona #1: Numrat e kundërt kanë module të barabarta, d.m.th. │а│=│- а│ Le të tregojmë se barazia është e vërtetë. Le të shkruajmë përkufizimin e numrit - A : │- a│= (2) Le të krahasojmë grupet (1) dhe (2). Natyrisht, përkufizimet e vlerave absolute të numrave Seksioni 1. Përcaktimi i vlerës absolute Dhe - A ndeshje. Prandaj, │а│=│- а│Kur shqyrtojmë veçoritë e mëposhtme, ne do të kufizohemi në formulimin e tyre, pasi prova e tyre është dhënë Prona #2: Vlera absolute e shumës së një numri të fundëm numrash realë nuk e kalon shumën e vlerave absolute të termave: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Prona #3: Vlera absolute e diferencës ndërmjet dy numrave realë nuk e kalon shumën e vlerave të tyre absolute: │а - │ ≤│а│+│в│ Prona #4: Vlera absolute e prodhimit të një numri të fundëm numrash realë është e barabartë me produktin e vlerave absolute të faktorëve: │а·в│=│а│·│в│ Prona #5: Vlera absolute e herësit të numrave realë është e barabartë me herësin e vlerave të tyre absolute:

Seksioni 3. Interpretimi gjeometrik i konceptit të modulit të një numri.
Çdo numër real mund të shoqërohet me një pikë në vijën numerike, e cila do të jetë një imazh gjeometrik i këtij numri real. Çdo pikë në vijën numerike i përgjigjet largësisë së saj nga origjina, d.m.th. gjatësia e segmentit nga origjina në pikën e dhënë. Kjo distancë konsiderohet gjithmonë si një vlerë jo negative. Prandaj, gjatësia e segmentit përkatës do të jetë interpretimi gjeometrik i vlerës absolute të një numri real të dhënë
Ilustrimi gjeometrik i paraqitur konfirmon qartë vetinë nr.1, d.m.th. moduli i numrave të kundërt janë të barabartë. Nga këtu vlefshmëria e barazisë kuptohet lehtësisht: │х – а│= │а – x│. Zgjidhja e ekuacionit │x│= m, ku m ≥ 0, përkatësisht x 1,2 = ± m, bëhet gjithashtu më e dukshme. Shembuj: 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
 x 1,2 = 2; 4
x 1,2 = 2; 4 Seksioni 4. Grafiku i funksionit y = │x│
Domeni i këtij funksioni janë të gjithë numrat realë.Seksioni 5. Konventat.
Në të ardhmen, kur shqyrtohen shembuj të zgjidhjes së ekuacioneve, do të përdoren konventat e mëposhtme: ( - shenja e sistemit [ - shenja e tërësisë Kur zgjidhet një sistem ekuacionesh (pabarazish), gjendet kryqëzimi i zgjidhjeve të ekuacioneve (pabarazive) të përfshira në sistem. Gjatë zgjidhjes së një grupi ekuacionesh (pabarazish), gjendet bashkimi i zgjidhjeve të përfshira në bashkësinë e ekuacioneve (pabarazitë).Kapitulli 2. Zgjidhja e ekuacioneve që përmbajnë një modul.
Në këtë kapitull do të shikojmë metodat algjebrike për zgjidhjen e ekuacioneve që përmbajnë një ose më shumë module.Seksioni 1. Ekuacionet e formës │F (x)│= m
Një ekuacion i këtij lloji quhet më i thjeshtë. Ai ka një zgjidhje nëse dhe vetëm nëse m ≥ 0. Sipas përcaktimit të modulit, ekuacioni origjinal është i barabartë me një grup prej dy ekuacionesh: │ F(x)│=m
 Shembuj:
Shembuj:
№1. Zgjidheni ekuacionin: │7х - 2│= 9


 Përgjigje: x 1
= - 1; X 2
= 1
4
/
7
№2
Përgjigje: x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1

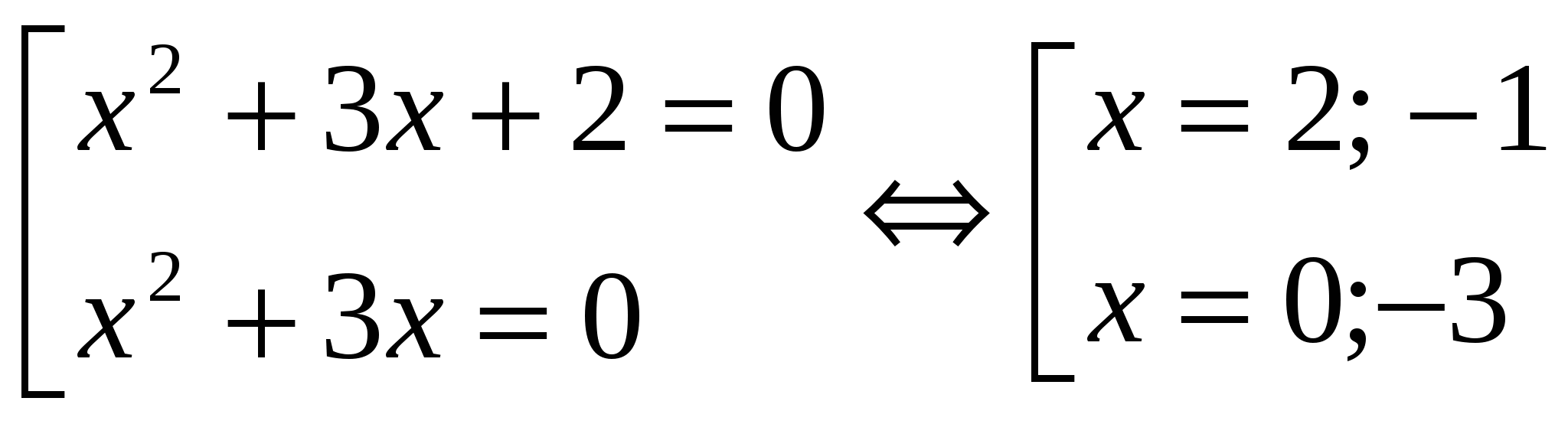 x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Përgjigje: shuma e rrënjëve është - 2.№3
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Përgjigje: shuma e rrënjëve është - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 le të shënojmë x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 - të dyja vlerat plotësojnë kushtin m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Përgjigje: numri i rrënjëve të ekuacionit 7. Ushtrime:
№1. Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve: │х - 5│= 3 №2 . Zgjidheni ekuacionin dhe tregoni rrënjën më të vogël: │x 2 + x│= 0 №3 . Zgjidheni ekuacionin dhe tregoni rrënjën më të madhe: │x 2 – 5x + 4│= 4 №4 .Zgjidhni ekuacionin dhe tregoni rrënjën e plotë: │2x 2 – 7x + 6│= 1 №5 .Zgjidhni ekuacionin dhe tregoni numrin e rrënjëve: │x 4 – 13x 2 + 50│= 14
Seksioni 2. Ekuacionet e formës F(│х│) = m
Argumenti i funksionit në anën e majtë është nën shenjën e modulit, dhe ana e djathtë është e pavarur nga ndryshorja. Le të shqyrtojmë dy mënyra për të zgjidhur ekuacione të këtij lloji. 1 mënyrë: Sipas përkufizimit të vlerës absolute, ekuacioni origjinal është i barabartë me kombinimin e dy sistemeve. Në secilën prej të cilave një kusht i imponohet një shprehjeje nënmodulare. F(│х│) =m Meqenëse funksioni F(│x│) është çift në të gjithë domenin e përkufizimit, rrënjët e ekuacioneve F(x) = m dhe F(- x) = m janë çifte numrash të kundërt. Prandaj, mjafton të zgjidhet një nga sistemet (kur shqyrtohen shembuj në këtë mënyrë, do të jepet një zgjidhje për një sistem). Metoda 2: Zbatimi i metodës së prezantimit të një ndryshoreje të re. Në këtë rast, futet emërtimi │x│= a, ku a ≥ 0. Kjo metodë është më pak voluminoze në dizajn.
Meqenëse funksioni F(│x│) është çift në të gjithë domenin e përkufizimit, rrënjët e ekuacioneve F(x) = m dhe F(- x) = m janë çifte numrash të kundërt. Prandaj, mjafton të zgjidhet një nga sistemet (kur shqyrtohen shembuj në këtë mënyrë, do të jepet një zgjidhje për një sistem). Metoda 2: Zbatimi i metodës së prezantimit të një ndryshoreje të re. Në këtë rast, futet emërtimi │x│= a, ku a ≥ 0. Kjo metodë është më pak voluminoze në dizajn. Shembuj: №1 . Zgjidheni ekuacionin: 3x 2 – 4│x│= - 1 Le të përdorim prezantimin e një ndryshoreje të re. Le të shënojmë │x│= a, ku a ≥ 0. Marrim ekuacionin 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Kthehemi në variablin origjinal: │ x│=1 dhe │х│= 1/3. Çdo ekuacion ka dy rrënjë. Përgjigje: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Zgjidhe ekuacionin: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
 Le të gjejmë zgjidhjen për sistemin e parë të popullsisë: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Vini re se x 2 nuk kënaq kushti x ≥ 0. Zgjidhje sistemi i dytë do të jetë numri i kundërt me vlerën x 1. Përgjigje: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Zgjidheni ekuacionin: x 4 – │х│= 0 Le të shënojmë │х│= a, ku a ≥ 0. Marrim ekuacionin a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Kthehu në variablin origjinal: │х│=0 dhe │х│= 1 x = 0; ± 1 Përgjigje: x 1
= 0; X 2
= 1; X 3
= - 1.
Le të gjejmë zgjidhjen për sistemin e parë të popullsisë: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Vini re se x 2 nuk kënaq kushti x ≥ 0. Zgjidhje sistemi i dytë do të jetë numri i kundërt me vlerën x 1. Përgjigje: x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Zgjidheni ekuacionin: x 4 – │х│= 0 Le të shënojmë │х│= a, ku a ≥ 0. Marrim ekuacionin a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Kthehu në variablin origjinal: │х│=0 dhe │х│= 1 x = 0; ± 1 Përgjigje: x 1
= 0; X 2
= 1; X 3
= - 1.
Ushtrime: №6. Zgjidheni ekuacionin: 2│х│ - 4.5 = 5 – 3 / 8 │х│ №7 . Zgjidheni ekuacionin, tregoni numrin e rrënjëve në përgjigjen tuaj: 3x 2 - 7│x│ + 2 = 0 №8 . Zgjidheni ekuacionin, tregoni zgjidhjet me numra të plotë në përgjigjen tuaj: x 4 + │x│ - 2 = 0
Seksioni 3. Ekuacionet e formës │F(x)│ = G(x)
Ana e djathtë e një ekuacioni të këtij lloji varet nga një ndryshore dhe, për rrjedhojë, ka një zgjidhje nëse dhe vetëm nëse ana e djathtë është një funksion G(x) ≥ 0. Ekuacioni origjinal mund të zgjidhet në dy mënyra : 1 mënyrë: Standard, i bazuar në zbulimin e një moduli bazuar në përkufizimin e tij dhe përbëhet nga një kalim ekuivalent në një kombinim të dy sistemeve. │ F(x)│ =G(X)
 Kjo metodë mund të përdoret në mënyrë racionale në rastin e një shprehjeje komplekse për funksionin G(x) dhe një më pak komplekse për funksionin F(x), pasi supozohet se pabarazitë me funksionin F(x) do të zgjidhen. Metoda 2: Konsiston në kalimin në një sistem ekuivalent në të cilin një kusht vendoset në anën e djathtë. │ F(x)│=
G(x)
Kjo metodë mund të përdoret në mënyrë racionale në rastin e një shprehjeje komplekse për funksionin G(x) dhe një më pak komplekse për funksionin F(x), pasi supozohet se pabarazitë me funksionin F(x) do të zgjidhen. Metoda 2: Konsiston në kalimin në një sistem ekuivalent në të cilin një kusht vendoset në anën e djathtë. │ F(x)│=
G(x)

 Kjo metodë është më e përshtatshme për t'u përdorur nëse shprehja për funksionin G(x) është më pak komplekse sesa për funksionin F(x), pasi zgjidhja e pabarazisë G(x) ≥ 0 supozohet gjithashtu në rast nga disa module, rekomandohet përdorimi i opsionit të dytë. Shembuj:
№1.
Zgjidheni ekuacionin: │x + 2│= 6 -2x
Kjo metodë është më e përshtatshme për t'u përdorur nëse shprehja për funksionin G(x) është më pak komplekse sesa për funksionin F(x), pasi zgjidhja e pabarazisë G(x) ≥ 0 supozohet gjithashtu në rast nga disa module, rekomandohet përdorimi i opsionit të dytë. Shembuj:
№1.
Zgjidheni ekuacionin: │x + 2│= 6 -2x  (1 mënyrë) Përgjigje: x = 1 1
/
3
№2.
(1 mënyrë) Përgjigje: x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
 (2 mënyra) Përgjigje: Prodhimi i rrënjëve është 3.
(2 mënyra) Përgjigje: Prodhimi i rrënjëve është 3.№3. Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj:
│x - 6│= x 2 - 5x + 9

Përgjigje: shuma e rrënjëve është 4.
Ushtrime: №9. │x + 4│= - 3x №10. Zgjidheni ekuacionin, tregoni numrin e zgjidhjeve në përgjigjen tuaj:│x 2 + x - 1│= 2x – 1 №11 . Zgjidheni ekuacionin, tregoni prodhimin e rrënjëve në përgjigjen tuaj:│x + 3│= x 2 + x – 6
Seksioni 4. Ekuacionet e formës │F(x)│= F(x) dhe │F(x)│= - F(x)
Ekuacionet e këtij lloji nganjëherë quhen "më të bukurat". Meqenëse ana e djathtë e ekuacioneve varet nga ndryshorja, zgjidhjet ekzistojnë nëse dhe vetëm nëse ana e djathtë është jo negative. Prandaj, ekuacionet origjinale janë ekuivalente me pabarazitë:│F(x)│= F(x) F(x) ≥ 0 dhe │F(x)│= - F(x) F(x) Shembuj: №1 . Zgjidheni ekuacionin, tregoni rrënjën e plotë më të vogël në përgjigjen tuaj: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Përgjigje: x = 1№2. Zgjidheni ekuacionin, tregoni gjatësinë e intervalit në përgjigjen tuaj: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Përgjigje: gjatësia e intervalit është 6.№3 . Zgjidheni ekuacionin dhe tregoni numrin e zgjidhjeve me numra të plotë në përgjigjen tuaj: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Përgjigje: 4 zgjidhje të plota.№4 . Zgjidheni ekuacionin dhe tregoni rrënjën më të madhe në përgjigjen tuaj:
│4 – x -
 │= 4 – x –
│= 4 – x –  x 2 – 5x + 5 = 0 D = 5 x 1,2 =
x 2 – 5x + 5 = 0 D = 5 x 1,2 =  ≈ 1,4
≈ 1,4Përgjigje: x = 3.
Ushtrime:
№12.
Zgjidheni ekuacionin, tregoni rrënjën e plotë në përgjigjen tuaj: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Zgjidheni ekuacionin, tregoni numrin e zgjidhjeve me numra të plotë në përgjigjen tuaj: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Zgjidheni ekuacionin në përgjigjen tuaj, tregoni një numër të plotë që nuk është rrënja e ekuacionit: 
Seksioni 5. Ekuacionet e formës │F(x)│= │G(x)│
Meqenëse të dyja anët e ekuacionit janë jonegative, zgjidhja përfshin shqyrtimin e dy rasteve: shprehjet nënmodulare janë të barabarta ose të kundërta në shenjë. Prandaj, ekuacioni origjinal është i barabartë me kombinimin e dy ekuacioneve: │ F(x)│= │ G(x)│ Shembuj:
№1.
Zgjidheni ekuacionin, tregoni rrënjën e plotë në përgjigjen tuaj: │x + 3│=│2x - 1│
Shembuj:
№1.
Zgjidheni ekuacionin, tregoni rrënjën e plotë në përgjigjen tuaj: │x + 3│=│2x - 1│  Përgjigje: rrënjë e plotë x = 4.№2.
Zgjidhe ekuacionin: │
x – x 2 - 1│=│2x – 3 – x 2 │
Përgjigje: rrënjë e plotë x = 4.№2.
Zgjidhe ekuacionin: │
x – x 2 - 1│=│2x – 3 – x 2 │  Përgjigje: x = 2.№3
.
Zgjidheni ekuacionin dhe tregoni produktin e rrënjëve në përgjigjen tuaj:
Përgjigje: x = 2.№3
.
Zgjidheni ekuacionin dhe tregoni produktin e rrënjëve në përgjigjen tuaj: 


 Ekuacionet rrënjësore 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 Përgjigje: prodhimi i rrënjëve është – 0,25. Ushtrime:
№15
. Zgjidheni ekuacionin dhe tregoni zgjidhjen e plotë në përgjigjen tuaj: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Zgjidheni ekuacionin, tregoni rrënjën më të vogël në përgjigjen tuaj:│5x - 3│=│7 - x│ №17
. Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj:
Ekuacionet rrënjësore 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 Përgjigje: prodhimi i rrënjëve është – 0,25. Ushtrime:
№15
. Zgjidheni ekuacionin dhe tregoni zgjidhjen e plotë në përgjigjen tuaj: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Zgjidheni ekuacionin, tregoni rrënjën më të vogël në përgjigjen tuaj:│5x - 3│=│7 - x│ №17
. Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj: 
Seksioni 6. Shembuj të zgjidhjes së ekuacioneve jo standarde
Në këtë seksion do të shqyrtojmë shembuj të ekuacioneve jo standarde, kur zgjidhim të cilat vlera absolute e shprehjes zbulohet me përkufizim. Shembuj:№1.
Zgjidheni ekuacionin, tregoni shumën e rrënjëve në përgjigjen tuaj: x · │x│- 5x – 6 = 0  Përgjigje: shuma e rrënjëve është 1 №2.
.
Zgjidheni ekuacionin, tregoni rrënjën më të vogël në përgjigjen tuaj: x 2 - 4x ·
Përgjigje: shuma e rrënjëve është 1 №2.
.
Zgjidheni ekuacionin, tregoni rrënjën më të vogël në përgjigjen tuaj: x 2 - 4x ·  - 5 = 0
- 5 = 0  Përgjigje: rrënjë më e vogël x = - 5. №3.
Zgjidhe ekuacionin:
Përgjigje: rrënjë më e vogël x = - 5. №3.
Zgjidhe ekuacionin:  Përgjigje: x = -1. Ushtrime:
№18.
Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve: x · │3x + 5│= 3x 2 + 4x + 3
Përgjigje: x = -1. Ushtrime:
№18.
Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve: x · │3x + 5│= 3x 2 + 4x + 3
№19.
Zgjidheni ekuacionin: x 2 – 3x = 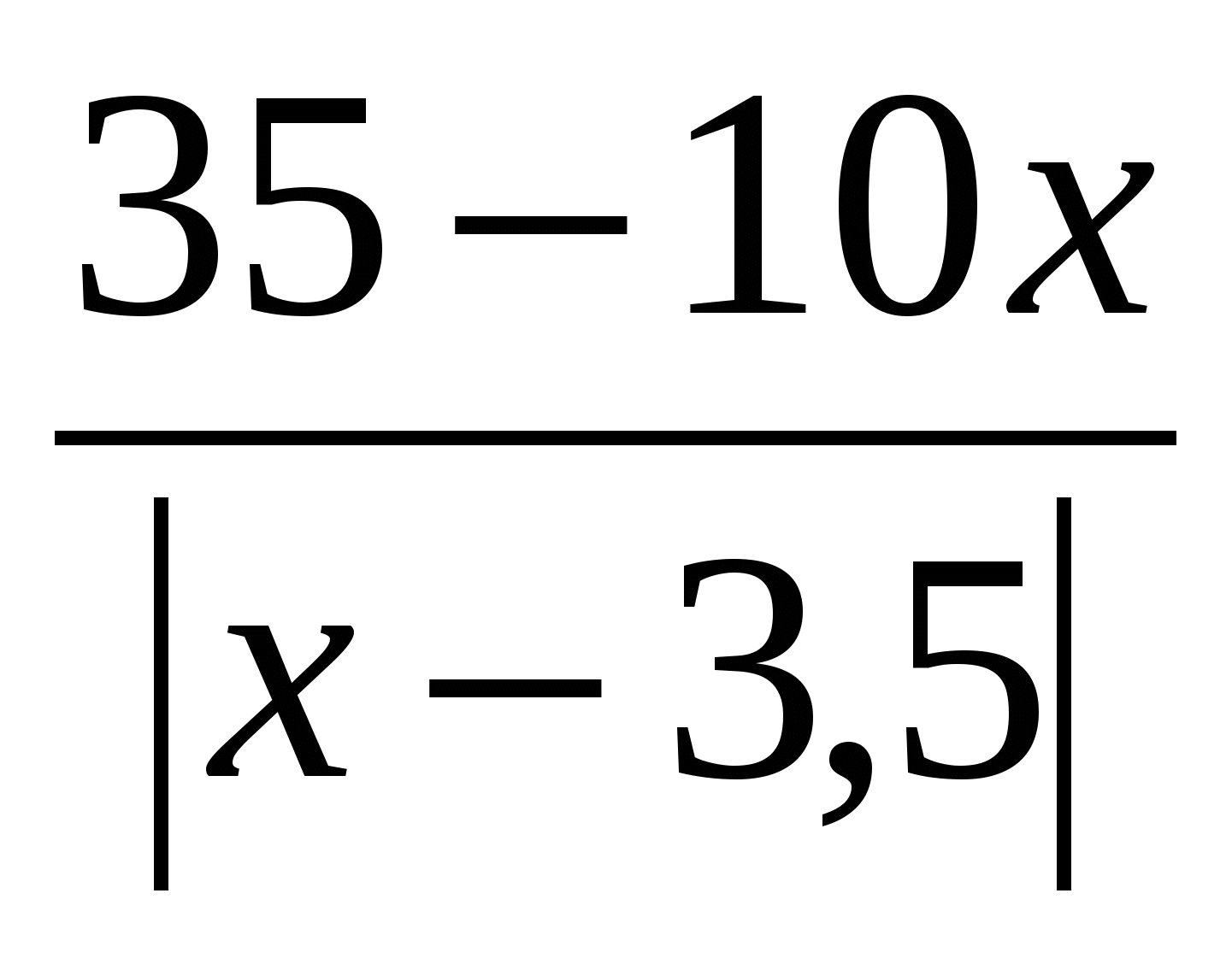
№20.
Zgjidhe ekuacionin: 
Seksioni 7. Ekuacionet e formës │F(x)│+│G(x)│=0
Është e lehtë të vërehet se në anën e majtë të ekuacionit të këtij lloji është shuma e madhësive jo negative. Prandaj, ekuacioni origjinal ka një zgjidhje nëse dhe vetëm nëse të dy termat janë të barabartë me zero në të njëjtën kohë. Ekuacioni është i barabartë me sistemin e ekuacioneve: │ F(x)│+│ G(x)│=0 Shembuj:
№1
. Zgjidhe ekuacionin:
Shembuj:
№1
. Zgjidhe ekuacionin:  Përgjigje: x = 2. №2.
Zgjidhe ekuacionin: Përgjigje: x = 1. Ushtrime:
№21.
Zgjidhe ekuacionin: №22
. Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj: №23
. Zgjidheni ekuacionin dhe tregoni numrin e zgjidhjeve në përgjigjen tuaj:
Përgjigje: x = 2. №2.
Zgjidhe ekuacionin: Përgjigje: x = 1. Ushtrime:
№21.
Zgjidhe ekuacionin: №22
. Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj: №23
. Zgjidheni ekuacionin dhe tregoni numrin e zgjidhjeve në përgjigjen tuaj: Seksioni 8. Ekuacionet e formës │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m
Për zgjidhjen e ekuacioneve të këtij lloji përdoret metoda e intervalit. Nëse e zgjidhim atë me zgjerim sekuencial të moduleve, marrim n grupe sistemesh, gjë që është shumë e rëndë dhe e papërshtatshme. Le të shqyrtojmë algoritmin e metodës së intervalit: 1). Gjeni vlerat e variablave X, për të cilin çdo modul është i barabartë me zero (zero të shprehjeve nënmodulare): 2). Shënoni vlerat e gjetura në një rresht numerik, i cili ndahet në intervale (numri i intervaleve është përkatësisht i barabartë me n+1
) 3). Përcaktoni se me çfarë shenje zbulohet secili modul në secilën prej intervaleve të marra (kur bëni një zgjidhje, mund të përdorni një rresht numerik, duke shënuar shenjat në të) 4). Ekuacioni origjinal është i barabartë me agregatin n+1
sisteme, në secilën prej të cilave tregohet anëtarësia e ndryshores X një nga intervalet. Shembuj:
№1
. Zgjidheni ekuacionin dhe tregoni rrënjën më të madhe në përgjigjen tuaj:
2). Shënoni vlerat e gjetura në një rresht numerik, i cili ndahet në intervale (numri i intervaleve është përkatësisht i barabartë me n+1
) 3). Përcaktoni se me çfarë shenje zbulohet secili modul në secilën prej intervaleve të marra (kur bëni një zgjidhje, mund të përdorni një rresht numerik, duke shënuar shenjat në të) 4). Ekuacioni origjinal është i barabartë me agregatin n+1
sisteme, në secilën prej të cilave tregohet anëtarësia e ndryshores X një nga intervalet. Shembuj:
№1
. Zgjidheni ekuacionin dhe tregoni rrënjën më të madhe në përgjigjen tuaj:  1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 2; x = -3 2). Le të shënojmë vlerat e gjetura në vijën numerike dhe të përcaktojmë se me çfarë shenje zbulohet secili modul në intervalet që rezultojnë:
1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 2; x = -3 2). Le të shënojmë vlerat e gjetura në vijën numerike dhe të përcaktojmë se me çfarë shenje zbulohet secili modul në intervalet që rezultojnë: x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
 - nuk ka zgjidhje Ekuacioni ka dy rrënjë. Përgjigje: rrënja më e madhe x = 2. №2.
Zgjidheni ekuacionin dhe jepni rrënjën e plotë në përgjigjen tuaj:
- nuk ka zgjidhje Ekuacioni ka dy rrënjë. Përgjigje: rrënja më e madhe x = 2. №2.
Zgjidheni ekuacionin dhe jepni rrënjën e plotë në përgjigjen tuaj:  1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 1,5; x = - 1 2). Le të shënojmë vlerat e gjetura në vijën numerike dhe të përcaktojmë se me çfarë shenje zbulohet secili modul në intervalet që rezultojnë: x + 1 x + 1 x + 1 - + +
1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 1,5; x = - 1 2). Le të shënojmë vlerat e gjetura në vijën numerike dhe të përcaktojmë se me çfarë shenje zbulohet secili modul në intervalet që rezultojnë: x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
 Sistemi i fundit nuk ka zgjidhje, prandaj ekuacioni ka dy rrënjë. Kur zgjidhni ekuacionin, duhet t'i kushtoni vëmendje shenjës "-" përpara modulit të dytë. Përgjigje: rrënjë e plotë x = 7. №3.
Zgjidheni ekuacionin, tregoni shumën e rrënjëve në përgjigjen tuaj: 1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 5; x = 1; x = - 2 2). Le të shënojmë vlerat e gjetura në vijën numerike dhe të përcaktojmë se me çfarë shenje zbulohet secili modul në intervalet që rezultojnë: x – 5 x – 5 x – 5 x – 5 - - - +
Sistemi i fundit nuk ka zgjidhje, prandaj ekuacioni ka dy rrënjë. Kur zgjidhni ekuacionin, duhet t'i kushtoni vëmendje shenjës "-" përpara modulit të dytë. Përgjigje: rrënjë e plotë x = 7. №3.
Zgjidheni ekuacionin, tregoni shumën e rrënjëve në përgjigjen tuaj: 1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 5; x = 1; x = - 2 2). Le të shënojmë vlerat e gjetura në vijën numerike dhe të përcaktojmë se me çfarë shenje zbulohet secili modul në intervalet që rezultojnë: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
 Ekuacioni ka dy rrënjë x = 0 dhe 2. Përgjigje: shuma e rrënjëve është 2. №4
.
Zgjidheni ekuacionin: 1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 1; x = 2; x = 3. 2). Le të përcaktojmë se me çfarë shenje zbulohet çdo modul në intervalet që rezultojnë. 3).
Ekuacioni ka dy rrënjë x = 0 dhe 2. Përgjigje: shuma e rrënjëve është 2. №4
.
Zgjidheni ekuacionin: 1). Le të gjejmë zerot e shprehjeve nënmodulare: x = 1; x = 2; x = 3. 2). Le të përcaktojmë se me çfarë shenje zbulohet çdo modul në intervalet që rezultojnë. 3).  Le të kombinojmë zgjidhjet e tre sistemeve të para. Përgjigje: ; x = 5.
Le të kombinojmë zgjidhjet e tre sistemeve të para. Përgjigje: ; x = 5.Ushtrime: №24. Zgjidhe ekuacionin:
 №25.
Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj: №26.
Zgjidheni ekuacionin dhe tregoni rrënjën më të vogël në përgjigjen tuaj: №27.
Zgjidheni ekuacionin dhe tregoni rrënjën më të madhe në përgjigjen tuaj:
№25.
Zgjidheni ekuacionin dhe tregoni shumën e rrënjëve në përgjigjen tuaj: №26.
Zgjidheni ekuacionin dhe tregoni rrënjën më të vogël në përgjigjen tuaj: №27.
Zgjidheni ekuacionin dhe tregoni rrënjën më të madhe në përgjigjen tuaj: Seksioni 9. Ekuacionet që përmbajnë disa module
Ekuacionet që përmbajnë module të shumta supozojnë praninë e vlerave absolute në shprehjet nënmodulare. Parimi bazë për zgjidhjen e ekuacioneve të këtij lloji është zbulimi sekuencial i moduleve, duke filluar nga ai "i jashtëm". Gjatë zgjidhjes, përdoren teknikat e diskutuara në seksionet nr.1, nr.3.Shembuj:
№1.
Zgjidhe ekuacionin:  Përgjigje: x = 1; - 11. №2.
Zgjidhe ekuacionin:
Përgjigje: x = 1; - 11. №2.
Zgjidhe ekuacionin:
Përgjigje: x = 0; 4; - 4. №3.
Zgjidheni ekuacionin dhe tregoni produktin e rrënjëve në përgjigjen tuaj:  Përgjigje: prodhimi i rrënjëve është – 8. №4.
Zgjidhe ekuacionin:
Përgjigje: prodhimi i rrënjëve është – 8. №4.
Zgjidhe ekuacionin:  Le të shënojmë ekuacionet e popullsisë (1)
Dhe (2)
dhe merrni parasysh zgjidhjen për secilën prej tyre veç e veç për lehtësinë e projektimit. Meqenëse të dy ekuacionet përmbajnë më shumë se një modul, është më e përshtatshme të kryhet një kalim ekuivalent në grupe sistemesh. (1)
Le të shënojmë ekuacionet e popullsisë (1)
Dhe (2)
dhe merrni parasysh zgjidhjen për secilën prej tyre veç e veç për lehtësinë e projektimit. Meqenëse të dy ekuacionet përmbajnë më shumë se një modul, është më e përshtatshme të kryhet një kalim ekuivalent në grupe sistemesh. (1)

 (2)
(2)


 Përgjigje:
Përgjigje:
Ushtrime:
№36.
Zgjidheni ekuacionin, tregoni shumën e rrënjëve në përgjigjen tuaj: 5 │3x-5│ = 25 x №37.
Zgjidheni ekuacionin, nëse ka më shumë se një rrënjë, tregoni shumën e rrënjëve në përgjigjen tuaj: │x + 2│ x – 3x – 10 = 1 №38.
Zgjidhe ekuacionin: 3 │2x -4│ = 9 │x│ №39.
Zgjidheni ekuacionin, në përgjigjen tuaj tregoni numrin e rrënjëve për: 2 │ sin x│ = √2 №40
. Zgjidheni ekuacionin dhe tregoni numrin e rrënjëve në përgjigjen tuaj:
Seksioni 3. Ekuacionet logaritmike.
Para se të zgjidhen ekuacionet e mëposhtme, është e nevojshme të rishikohen vetitë e logaritmeve dhe funksioni logaritmik. Shembuj: №1. Zgjidheni ekuacionin, tregoni prodhimin e rrënjëve në përgjigjen tuaj: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1Rasti 1: nëse x ≥ - 1, atëherë log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – plotëson kushtin x ≥ - 1 2 rasti: nëse x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 - plotëson kushtin x - 1
Përgjigje: prodhimi i rrënjëve është – 15.
№2.
Zgjidheni ekuacionin, tregoni shumën e rrënjëve në përgjigjen tuaj: lg  O.D.Z.
O.D.Z. 



Përgjigje: shuma e rrënjëve është 0,5.
№3.
Zgjidheni ekuacionin: log 5  O.D.Z.
O.D.Z. 
 Përgjigje: x = 9. №4.
Zgjidheni ekuacionin: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Le të përdorim formulën për të kaluar në një bazë tjetër. │2 - log 5 x│+ 3 = │1 + log 5 x│
Përgjigje: x = 9. №4.
Zgjidheni ekuacionin: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Le të përdorim formulën për të kaluar në një bazë tjetër. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Të gjejmë zerot e shprehjeve nënmodulare: x = 25; x = Këta numra ndajnë gamën e vlerave të pranueshme në tre intervale, kështu që ekuacioni është i barabartë me një grup prej tre sistemesh.  Përgjigje:
Përgjigje:
Një fakt tjetër i rëndësishëm: moduli nuk është kurrë negativ. Çfarëdo numri që marrim - qoftë pozitiv apo negativ - moduli i tij gjithmonë rezulton pozitiv (ose, në raste ekstreme, zero). Kjo është arsyeja pse moduli shpesh quhet vlerë absolute e një numri.
Përveç kësaj, nëse kombinojmë përkufizimin e modulit për një numër pozitiv dhe negativ, marrim një përkufizim global të modulit për të gjithë numrat. Domethënë: moduli i një numri është i barabartë me vetë numrin nëse numri është pozitiv (ose zero), ose i barabartë me numrin e kundërt nëse numri është negativ. Ju mund ta shkruani këtë si formulë:
Ekziston edhe një modul zero, por ai është gjithmonë i barabartë me zero. Përveç kësaj, zero është i vetmi numër që nuk ka një të kundërt.
Kështu, nëse marrim parasysh funksionin $y=\left| x \right|$ dhe përpiquni të vizatoni grafikun e tij, do të merrni diçka të tillë:
Grafiku i modulit dhe shembulli i zgjidhjes së ekuacionit
Nga kjo foto është menjëherë e qartë se $\left| -m \djathtas|=\majtas| m \right|$, dhe grafiku i modulit nuk bie kurrë nën boshtin x. Por kjo nuk është e gjitha: vija e kuqe shënon vijën e drejtë $y=a$, e cila, për $a$ pozitive, na jep dy rrënjë njëherësh: $((x)_(1))$ dhe $((x) _(2)) $, por ne do të flasim për këtë më vonë.
Përveç përkufizimit thjesht algjebrik, ekziston edhe një përkufizim gjeometrik. Le të themi se ka dy pika në vijën numerike: $((x)_(1))$ dhe $((x)_(2))$. Në këtë rast, shprehja $\left| ((x)_(1))-((x)_(2)) \right|$ është thjesht distanca ndërmjet pikave të specifikuara. Ose, nëse preferoni, gjatësia e segmentit që lidh këto pika:
 Moduli është distanca midis pikave në një vijë numerike
Moduli është distanca midis pikave në një vijë numerike Ky përkufizim gjithashtu nënkupton që moduli është gjithmonë jo negativ. Por mjaft përkufizime dhe teori - le të kalojmë në ekuacione reale.
Formula bazë
Mirë, ne e kemi rregulluar përkufizimin. Por kjo nuk e bëri më të lehtë. Si të zgjidhen ekuacionet që përmbajnë pikërisht këtë modul?
Qetë, vetëm qetë. Le të fillojmë me gjërat më të thjeshta. Konsideroni diçka si kjo:
\[\majtas| x\djathtas|=3\]
Pra, moduli i $x$ është 3. Me çfarë mund të jetë i barabartë $x$? Epo, duke gjykuar nga përkufizimi, ne jemi mjaft të kënaqur me $x=3$. Vërtet:
\[\majtas| 3\djathtas|=3\]
A ka numra të tjerë? Cap duket se është duke lënë të kuptohet se ka. Për shembull, $x=-3$ është gjithashtu $\left| -3 \djathtas|=3$, d.m.th. plotësohet barazia e kërkuar.
Pra, ndoshta nëse kërkojmë dhe mendojmë, do të gjejmë më shumë numra? Por le ta pranojmë: nuk ka më numra. Ekuacioni $\majtas| x \right|=3$ ka vetëm dy rrënjë: $x=3$ dhe $x=-3$.
Tani le ta komplikojmë pak detyrën. Lëreni funksionin $f\left(x \djathtas)$ të varet nën shenjën e modulit në vend të ndryshores $x$ dhe vendosni një numër arbitrar $a$ në vend të treshes në të djathtë. Ne marrim ekuacionin:
\[\majtas| f\majtas(x \djathtas) \djathtas|=a\]
Pra, si mund ta zgjidhim këtë? Më lejoni t'ju kujtoj: $f\left(x \right)$ është një funksion arbitrar, $a$ është çdo numër. Ato. Gjithçka fare! Për shembull:
\[\majtas| 2x+1 \djathtas|=5\]
\[\majtas| 10x-5 \djathtas|=-65\]
Le t'i kushtojmë vëmendje ekuacionit të dytë. Mund të thuash menjëherë për të: ai nuk ka rrënjë. Pse? Gjithçka është e saktë: sepse kërkon që moduli të jetë i barabartë me një numër negativ, gjë që nuk ndodh kurrë, pasi ne tashmë e dimë që moduli është gjithmonë një numër pozitiv ose, në raste ekstreme, zero.
Por me ekuacionin e parë gjithçka është më argëtuese. Ka dy opsione: ose ka një shprehje pozitive nën shenjën e modulit, dhe më pas $\left| 2x+1 \right|=2x+1$, ose kjo shprehje është ende negative, dhe më pas $\left| 2x+1 \djathtas|=-\majtas(2x+1 \djathtas)=-2x-1$. Në rastin e parë, ekuacioni ynë do të rishkruhet si më poshtë:
\[\majtas| 2x+1 \djathtas|=5\Djathtas 2x+1=5\]
Dhe befas rezulton se shprehja submodulare $2x+1$ është vërtet pozitive - është e barabartë me numrin 5. Kjo është ne mund ta zgjidhim me siguri këtë ekuacion - rrënja që rezulton do të jetë një pjesë e përgjigjes:
Ata që janë veçanërisht mosbesues mund të përpiqen të zëvendësojnë rrënjën e gjetur në ekuacionin origjinal dhe të sigurohen që ka vërtet një numër pozitiv nën modul.
Tani le të shohim rastin e një shprehje negative submodulare:
\[\majtas\( \fillimi(rreshtoj)& \majtas| 2x+1 \djathtas|=5 \\& 2x+1 \lt 0 \\\fund (rreshtoj) \djathtas.\Rightarrow -2x-1=5 \Shigjeta djathtas 2x+1=-5\]
Oops! Përsëri, gjithçka është e qartë: ne supozuam se $2x+1 \lt 0$, dhe si rezultat morëm atë $2x+1=-5$ - në të vërtetë, kjo shprehje është më pak se zero. Ne zgjidhim ekuacionin që rezulton, ndërsa tashmë e dimë me siguri se rrënja e gjetur do të na përshtatet:
Në total, përsëri morëm dy përgjigje: $x=2$ dhe $x=3$. Po, sasia e llogaritjeve doli të jetë pak më e madhe se në ekuacionin shumë të thjeshtë $\left| x \right|=3$, por asgjë në thelb nuk ka ndryshuar. Pra, ndoshta ekziston një lloj algoritmi universal?
Po, ekziston një algoritëm i tillë. Dhe tani do ta analizojmë.
Largimi i shenjës së modulit
Le të na jepet ekuacioni $\left| f\left(x \right) \right|=a$, dhe $a\ge 0$ (përndryshe, siç e dimë tashmë, nuk ka rrënjë). Pastaj mund të heqësh qafe shenjën e modulit duke përdorur rregullin e mëposhtëm:
\[\majtas| f\majtas(x \djathtas) \djathtas|=a\Shigjeta djathtas f\majtas(x \djathtas)=\pm a\]
Kështu, ekuacioni ynë me një modul ndahet në dy, por pa një modul. Kjo është e gjitha teknologjia! Le të përpiqemi të zgjidhim disa ekuacione. Le të fillojmë me këtë
\[\majtas| 5x+4 \djathtas|=10\Djathtas shigjetë 5x+4=\pm 10\]
Le të shqyrtojmë veçmas kur ka një dhjetë plus në të djathtë, dhe veçmas kur ka një minus. Ne kemi:
\[\fillim(rreshtoj)& 5x+4=10\Djathtas shigjetë 5x=6\Djathtas shigjetë x=\frac(6)(5)=1,2; \\& 5x+4=-10\Djathtas 5x=-14\Djathtas x=-\frac(14)(5)=-2.8. \\\fund (rreshtoj)\]
Kjo është ajo! Ne morëm dy rrënjë: $x=1.2$ dhe $x=-2.8$. E gjithë zgjidhja mori fjalë për fjalë dy rreshta.
Ok, pa dyshim, le të shohim diçka pak më serioze:
\[\majtas| 7-5x\djathtas|=13\]
Përsëri hapim modulin me plus dhe minus:
\[\fillim(rreshtoj)& 7-5x=13\Djathtas -5x=6\Djathtas x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\\fund (rreshtoj)\]
Përsëri disa rreshta - dhe përgjigja është gati! Siç thashë, nuk ka asgjë të komplikuar në lidhje me modulet. Thjesht duhet të mbani mend disa rregulla. Prandaj, ne vazhdojmë dhe fillojmë me detyra vërtet më komplekse.
Rasti i një ndryshoreje në anën e djathtë
Tani merrni parasysh këtë ekuacion:
\[\majtas| 3x-2 \djathtas|=2x\]
Ky ekuacion është thelbësisht i ndryshëm nga të gjitha ato të mëparshme. Si? Dhe fakti që në të djathtë të shenjës së barazimit është shprehja $2x$ - dhe nuk mund ta dimë paraprakisht nëse është pozitive apo negative.
Çfarë duhet bërë në këtë rast? Së pari, duhet ta kuptojmë një herë e përgjithmonë nëse ana e djathtë e ekuacionit rezulton negative, atëherë ekuacioni nuk do të ketë rrënjë- ne tashmë e dimë se moduli nuk mund të jetë i barabartë me një numër negativ.
Dhe së dyti, nëse pjesa e djathtë është ende pozitive (ose e barabartë me zero), atëherë mund të veproni saktësisht në të njëjtën mënyrë si më parë: thjesht hapni modulin veçmas me një shenjë plus dhe veçmas me një shenjë minus.
Kështu, ne formulojmë një rregull për funksionet arbitrare $f\left(x \right)$ dhe $g\left(x \right)$:
\[\majtas| f\ majtas(x \djathtas) \djathtas|=g\majtas(x \djathtas)\Djathtas shigjeta \majtas\( \fillimi(rreshtoj)& f\majtë(x \djathtas)=\pm g\majtas (x \djathtas ), \\& g\majtas(x \djathtas)\ge 0. \\\fund (rreshtoj) \djathtas.\]
Në lidhje me ekuacionin tonë marrim:
\[\majtas| 3x-2 \djathtas|=2x\Djathtas shigjeta \majtas\( \fillimi(radhis)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\fund (rreshtoj) \djathtas.\]
Epo, ne do të përballojmë disi kërkesën $2x\ge 0$. Në fund, ne mund të zëvendësojmë marrëzi rrënjët që marrim nga ekuacioni i parë dhe të kontrollojmë nëse pabarazia vlen apo jo.
Pra, le të zgjidhim vetë ekuacionin:
\[\fillim(lidh)& 3x-2=2\Djathtas shigjetë 3x=4\Djathtas x=\frac(4)(3); \\& 3x-2=-2\Djathtas shigjetë 3x=0\Djathtas x=0. \\\fund (rreshtoj)\]
Epo, cila nga këto dy rrënjë plotëson kërkesën $2x\ge 0$? Po të dyja! Prandaj, përgjigja do të jetë dy numra: $x=(4)/(3)\;$ dhe $x=0$. Kjo është zgjidhja.
Dyshoj se disa nga studentët tashmë kanë filluar të mërziten? Epo, le të shohim një ekuacion edhe më kompleks:
\[\majtas| ((x)^(3))-3((x)^(2))+x \djathtas|=x-((x)^(3))\]
Edhe pse duket e keqe, në fakt është ende i njëjti ekuacion i formës "moduli është i barabartë me funksionin":
\[\majtas| f\majtas(x \djathtas) \djathtas|=g\majtas(x \djathtas)\]
Dhe zgjidhet saktësisht në të njëjtën mënyrë:
\[\majtas| ((x)^(3))-3((x)^(2))+x \djathtas|=x-((x)^(3))\Djathtas shigjeta \majtas\( \fillimi(rreshtoj)& ( (x)^(3))-3((x)^(2))+x=\pm \majtas(x-((x)^(3)) \djathtas), \\& x-((x )^(3))\ge 0. \\\fund (rreshtoj) \djathtas.\]
Ne do të merremi me pabarazinë më vonë - ajo është disi shumë e keqe (në fakt, është e thjeshtë, por ne nuk do ta zgjidhim atë). Tani për tani, është më mirë të merremi me ekuacionet që rezultojnë. Le të shqyrtojmë rastin e parë - kjo është kur moduli zgjerohet me një shenjë plus:
\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]
Epo, është e kotë që ju duhet të mbledhni gjithçka nga e majta, të sillni të ngjashme dhe të shihni se çfarë ndodh. Dhe kjo është ajo që ndodh:
\[\filloj(rreshtoj)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\fund (rreshtoj)\]
Ne nxjerrim faktorin e përbashkët $((x)^(2))$ nga kllapat dhe marrim një ekuacion shumë të thjeshtë:
\[((x)^(2))\majtas(2x-3 \djathtas)=0\Djathtas shigjeta \majtas[ \fillimi(rreshtoj)& ((x)^(2))=0 \\& 2x-3 =0 \\\fund (rreshtoj) \djathtas.\]
\[((x)_(1))=0;\katër ((x)_(2))=\frac(3)(2)=1,5.\]
Këtu kemi përfituar nga një veti e rëndësishme e produktit, për hir të së cilës kemi faktorizuar polinomin origjinal: produkti është i barabartë me zero kur të paktën një nga faktorët është i barabartë me zero.
Tani le të merremi me ekuacionin e dytë në të njëjtën mënyrë, i cili përftohet duke zgjeruar modulin me një shenjë minus:
\[\filloj(rreshtoj)& ((x)^(3))-3((x)^(2))+x=-\majtas(x-((x)^(3)) \djathtas); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\ majtas(-3x+2 \djathtas)=0. \\\fund (rreshtoj)\]
Përsëri e njëjta gjë: produkti është i barabartë me zero kur të paktën një nga faktorët është i barabartë me zero. Ne kemi:
\[\majtas[ \fillimi(rreshtoj)& x=0 \\& -3x+2=0 \\\fund (rreshtoj) \djathtas.\]
Epo, kemi marrë tre rrënjë: $x=0$, $x=1.5$ dhe $x=(2)/(3)\;$. Epo, cili nga ky grup do të hyjë në përgjigjen përfundimtare? Për ta bërë këtë, mbani mend se kemi një kufizim shtesë në formën e pabarazisë:
Si të merret parasysh kjo kërkesë? Le të zëvendësojmë vetëm rrënjët e gjetura dhe të kontrollojmë nëse pabarazia vlen për këto $x$ apo jo. Ne kemi:
\[\fillim(lidh)& x=0\Shigjeta djathtas x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Shigjeta djathtas x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Shigjeta djathtas x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\fund (rreshtoj)\]
Kështu, rrënja $x=1.5$ nuk na përshtatet. Dhe si përgjigje do të ketë vetëm dy rrënjë:
\[((x)_(1))=0;\katër ((x)_(2))=\frac(2)(3).\]
Siç mund ta shihni, edhe në këtë rast nuk kishte asgjë të komplikuar - ekuacionet me module zgjidhen gjithmonë duke përdorur një algoritëm. Ju vetëm duhet të keni një kuptim të mirë të polinomeve dhe pabarazive. Prandaj, ne kalojmë në detyra më komplekse - tashmë nuk do të ketë një, por dy module.
Ekuacionet me dy module
Deri më tani, ne kemi studiuar vetëm ekuacionet më të thjeshta - kishte një modul dhe diçka tjetër. E dërguam këtë “diçka tjetër” në një pjesë tjetër të pabarazisë, larg modulit, në mënyrë që në fund gjithçka të reduktohej në një ekuacion të formës $\left| f\left(x \right) \right|=g\left(x \djathtas)$ ose edhe më e thjeshtë $\majtas| f\left(x \djathtas) \djathtas|=a$.
Por kopshti i fëmijëve ka mbaruar - është koha të shqyrtojmë diçka më serioze. Le të fillojmë me ekuacione si kjo:
\[\majtas| f\left(x \djathtas) \djathtas|=\majtas| g\left(x \djathtas) \djathtas|\]
Ky është një ekuacion i formës "moduli është i barabartë me modulin". Pika thelbësisht e rëndësishme është mungesa e termave dhe faktorëve të tjerë: vetëm një modul në të majtë, një modul më shumë në të djathtë - dhe asgjë më shumë.
Dikush tani do të mendojë se ekuacione të tilla janë më të vështira për t'u zgjidhur sesa ato që kemi studiuar deri tani. Por jo: këto ekuacione janë edhe më të lehta për t'u zgjidhur. Këtu është formula:
\[\majtas| f\left(x \djathtas) \djathtas|=\majtas| g\majtas(x \djathtas) \djathtas|\Djathtas f\ majtas(x \djathtas)=\pm g\majtas(x \djathtas)\]
Të gjitha! Ne thjesht barazojmë shprehjet nënmodulare duke vendosur një shenjë plus ose minus përpara njërit prej tyre. Dhe pastaj ne zgjidhim dy ekuacionet që rezultojnë - dhe rrënjët janë gati! Asnjë kufizim shtesë, pa pabarazi, etj. Është shumë e thjeshtë.
Le të përpiqemi ta zgjidhim këtë problem:
\[\majtas| 2x+3 \djathtas|=\majtas| 2x-7 \djathtas|\]
Fillore, Watson! Zgjerimi i moduleve:
\[\majtas| 2x+3 \djathtas|=\majtas| 2x-7 \djathtas|\Djathtas 2x+3=\pm \majtas(2x-7 \djathtas)\]
Le të shqyrtojmë secilin rast veç e veç:
\[\fillim(lidh)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\majtas(2x-7 \djathtas)\Djathtas shigjetë 2x+3=-2x+7. \\\fund (rreshtoj)\]
Ekuacioni i parë nuk ka rrënjë. Sepse kur është $3=-7$? Në çfarë vlerash prej $x$? “Çfarë dreqin është $x$? Jeni të vrarë me gurë? Nuk ka fare $x$ atje, "thoni ju. Dhe do të kesh të drejtë. Ne kemi marrë një barazi që nuk varet nga ndryshorja $x$, dhe në të njëjtën kohë barazia në vetvete është e pasaktë. Kjo është arsyeja pse nuk ka rrënjë :)
Me ekuacionin e dytë, gjithçka është pak më interesante, por edhe shumë, shumë e thjeshtë:
Siç mund ta shihni, gjithçka u zgjidh fjalë për fjalë në disa rreshta - ne nuk prisnim asgjë tjetër nga një ekuacion linear.
Si rezultat, përgjigja përfundimtare është: $x=1$.
Pra, si? E veshtire? Sigurisht që jo. Le të provojmë diçka tjetër:
\[\majtas| x-1 \djathtas|=\majtas| ((x)^(2))-3x+2 \djathtas|\]
Përsëri kemi një ekuacion të formës $\left| f\left(x \djathtas) \djathtas|=\majtas| g\left(x \djathtas) \djathtas|$. Prandaj, ne e rishkruajmë menjëherë, duke zbuluar shenjën e modulit:
\[((x)^(2))-3x+2=\pm \majtas(x-1 \djathtas)\]
Ndoshta dikush do të pyesë tani: “Hej, çfarë marrëzie? Pse shfaqet "plus-minus" në shprehjen e djathtë dhe jo në të majtë?" Qetësohu, do të shpjegoj gjithçka tani. Në të vërtetë, në një mënyrë të mirë duhet ta kishim rishkruar ekuacionin tonë si më poshtë:
Pastaj duhet të hapni kllapat, të zhvendosni të gjithë termat në njërën anë të shenjës së barabartë (pasi ekuacioni, padyshim, do të jetë katror në të dyja rastet) dhe më pas gjeni rrënjët. Por duhet ta pranoni: kur "plus-minus" shfaqet para tre termave (veçanërisht kur njëri prej këtyre termave është një shprehje kuadratike), duket disi më e ndërlikuar sesa situata kur "plus-minus" shfaqet vetëm para dy termave.
Por asgjë nuk na pengon të rishkruajmë ekuacionin origjinal si më poshtë:
\[\majtas| x-1 \djathtas|=\majtas| ((x)^(2))-3x+2 \djathtas|\Djathtas shigjeta \majtas| ((x)^(2))-3x+2 \djathtas|=\majtas| x-1 \djathtas|\]
Çfarë ndodhi? Asgjë e veçantë: ata thjesht këmbyen anën e majtë dhe të djathtë. Një gjë e vogël që përfundimisht do ta bëjë jetën tonë pak më të lehtë :)
Në përgjithësi, ne e zgjidhim këtë ekuacion, duke marrë parasysh opsionet me një plus dhe një minus:
\[\fillo(rreshtoj)& ((x)^(2))-3x+2=x-1\Shigjeta djathtas ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\majtas(x-1 \djathtas)\Shigjeta djathtas ((x)^(2))-2x+1=0. \\\fund (rreshtoj)\]
Ekuacioni i parë ka rrënjë $x=3$ dhe $x=1$. E dyta është përgjithësisht një katror i saktë:
\[((x)^(2))-2x+1=((\majtas(x-1 \djathtas))^(2))\]
Prandaj, ajo ka vetëm një rrënjë: $x=1$. Por ne e kemi marrë tashmë këtë rrënjë më herët. Kështu, vetëm dy numra do të hyjnë në përgjigjen përfundimtare:
\[((x)_(1))=3;\katër ((x)_(2))=1.\]
Misioni i kryer! Mund të merrni një byrek nga rafti dhe ta hani. Janë 2 prej tyre, e juaja është e mesme.
Shënim i rëndësishëm. Prania e rrënjëve identike për variante të ndryshme të zgjerimit të modulit do të thotë që polinomet origjinale janë të faktorizuar dhe midis këtyre faktorëve do të ketë patjetër një të përbashkët. Vërtet:
\[\filloj(rreshtoj)& \majtas| x-1 \djathtas|=\majtas| ((x)^(2))-3x+2 \djathtas|; \\& \majtas| x-1 \djathtas|=\majtas| \majtas(x-1 \djathtas)\majtas(x-2 \djathtas) \djathtas|. \\\fund (rreshtoj)\]
Një nga vetitë e modulit: $\left| a\cdot b \djathtas|=\majtas| a \djathtas|\cdot \majtas| b \right|$ (d.m.th. moduli i produktit është i barabartë me produktin e modulit), kështu që ekuacioni origjinal mund të rishkruhet si më poshtë:
\[\majtas| x-1 \djathtas|=\majtas| x-1 \djathtas|\cdot \majtas| x-2 \djathtas|\]
Siç mund ta shihni, ne kemi vërtet një faktor të përbashkët. Tani, nëse mblidhni të gjitha modulet në njërën anë, mund ta hiqni këtë faktor nga kllapa:
\[\filloj(rreshtoj)& \majtas| x-1 \djathtas|=\majtas| x-1 \djathtas|\cdot \majtas| x-2 \djathtas|; \\& \majtas| x-1 \djathtas|-\majtas| x-1 \djathtas|\cdot \majtas| x-2 \djathtas|=0; \\& \majtas| x-1 \djathtas|\cdot \majtas(1-\majtas| x-2 \djathtas| \djathtas)=0. \\\fund (rreshtoj)\]
Epo, tani mbani mend se produkti është i barabartë me zero kur të paktën një nga faktorët është i barabartë me zero:
\[\majtas[ \filloj(rreshtoj)& \majtas| x-1 \djathtas|=0, \\& \majtas| x-2 \djathtas|=1. \\\fund (rreshtoj) \djathtas.\]
Kështu, ekuacioni origjinal me dy module është reduktuar në dy ekuacionet më të thjeshta për të cilat folëm që në fillim të mësimit. Ekuacione të tilla mund të zgjidhen fjalë për fjalë në disa rreshta.
Kjo vërejtje mund të duket e panevojshme komplekse dhe e pazbatueshme në praktikë. Megjithatë, në realitet, mund të hasni probleme shumë më komplekse se ato që po shohim sot. Në to modulet mund të kombinohen me polinome, rrënjë aritmetike, logaritme etj. Dhe në situata të tilla, aftësia për të ulur shkallën e përgjithshme të ekuacionit duke hequr diçka nga kllapat mund të jetë shumë, shumë e dobishme.
Tani do të doja të shikoja një ekuacion tjetër, i cili në pamje të parë mund të duket i çmendur. Shumë studentë ngecin në të, edhe ata që mendojnë se i kuptojnë mirë modulet.
Sidoqoftë, ky ekuacion është edhe më i lehtë për t'u zgjidhur sesa ai që pamë më parë. Dhe nëse e kuptoni pse, do të merrni një mashtrim tjetër për zgjidhjen e shpejtë të ekuacioneve me modul.
Pra, ekuacioni është:
\[\majtas| x-((x)^(3)) \djathtas|+\majtas| ((x)^(2))+x-2 \djathtas|=0\]
Jo, kjo nuk është një gabim shtypi: është një plus midis moduleve. Dhe ne duhet të gjejmë në çfarë $x$ shuma e dy moduleve është e barabartë me zero.
Cili është problemi gjithsesi? Por problemi është se çdo modul është një numër pozitiv, ose, në raste ekstreme, zero. Çfarë ndodh nëse shtoni dy numra pozitivë? Natyrisht një numër pozitiv përsëri:
\[\fillim(lidh)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\fund (rreshtoj)\]
Rreshti i fundit mund t'ju bëjë të mendoni: e vetmja herë kur shuma e moduleve është zero është nëse secili modul është zero:
\[\majtas| x-((x)^(3)) \djathtas|+\majtas| ((x)^(2))+x-2 \djathtas|=0\Djathtas shigjeta \majtas\( \fillimi(rreshtoj)& \majtas| x-((x)^(3)) \djathtas|=0, \\& \majtas| ((x)^(2)+x-2 \djathtas|=0.
Dhe kur moduli është i barabartë me zero? Vetëm në një rast - kur shprehja nënmodulare është e barabartë me zero:
\[((x)^(2))+x-2=0\Djathtas shigjeta \majtas(x+2 \djathtas)\majtas(x-1 \djathtas)=0\Shigjeta djathtas \majtas[ \fillimi(radhis)& x=-2 \\& x=1 \\\fund (rreshtoj) \djathtas.\]
Kështu, kemi tre pika në të cilat moduli i parë rivendoset në zero: 0, 1 dhe −1; si dhe dy pika në të cilat moduli i dytë rivendoset në zero: −2 dhe 1. Megjithatë, ne kemi nevojë që të dy modulet të rivendosen në zero në të njëjtën kohë, kështu që midis numrave të gjetur duhet të zgjedhim ata që përfshihen në të dy grupet. Natyrisht, ekziston vetëm një numër i tillë: $x=1$ - kjo do të jetë përgjigja përfundimtare.
Metoda e ndarjes
Epo, ne kemi mbuluar tashmë një mori problemesh dhe kemi mësuar shumë teknika. A mendoni se kjo është e gjitha? Por jo! Tani do të shikojmë teknikën përfundimtare - dhe në të njëjtën kohë më të rëndësishmen. Do të flasim për ndarjen e ekuacioneve me modul. Për çfarë do të flasim madje? Le të kthehemi pak prapa dhe të shohim një ekuacion të thjeshtë. Për shembull kjo:
\[\majtas| 3x-5 \djathtas|=5-3x\]
Në parim, ne tashmë dimë se si ta zgjidhim një ekuacion të tillë, sepse është një ndërtim standard i formës $\left| f\left(x \djathtas) \djathtas|=g\left(x \djathtas)$. Por le të përpiqemi ta shikojmë këtë ekuacion nga një kënd pak më ndryshe. Më saktësisht, merrni parasysh shprehjen nën shenjën e modulit. Më lejoni t'ju kujtoj se moduli i çdo numri mund të jetë i barabartë me vetë numrin, ose mund të jetë i kundërt me këtë numër:
\[\majtas| a \djathtas|=\majtas\( \fillimi(rreshtoj)& a,\katër a\ge 0, \\& -a,\katër a \lt 0. \\\fund (rreshtoj) \djathtas.\]
Në fakt, kjo paqartësi është i gjithë problemi: meqenëse numri nën modul ndryshon (kjo varet nga ndryshorja), nuk është e qartë për ne nëse është pozitiv apo negativ.
Por, çka nëse fillimisht kërkon që ky numër të jetë pozitiv? Për shembull, le të kërkojmë që $3x-5 \gt 0$ - në këtë rast ne jemi të garantuar të marrim një numër pozitiv nën shenjën e modulit, dhe ne mund ta heqim plotësisht këtë modul:
Kështu, ekuacioni ynë do të kthehet në një linear, i cili mund të zgjidhet lehtësisht:
Vërtetë, të gjitha këto mendime kanë kuptim vetëm nën kushtin $3x-5 \gt 0$ - ne vetë e prezantuam këtë kërkesë në mënyrë që të zbulojmë pa mëdyshje modulin. Prandaj, le të zëvendësojmë $x=\frac(5)(3)$ të gjetur në këtë gjendje dhe kontrollojmë:
Rezulton se për vlerën e specifikuar prej $x$ kërkesa jonë nuk është përmbushur, sepse shprehja doli të jetë e barabartë me zero, dhe ne kemi nevojë që ajo të jetë rreptësisht më e madhe se zero. E trishtueshme :(
Por është në rregull! Në fund të fundit, ekziston një opsion tjetër $3x-5 \lt 0$. Për më tepër: ekziston edhe rasti $3x-5=0$ - kjo gjithashtu duhet të merret parasysh, përndryshe zgjidhja do të jetë e paplotë. Pra, merrni parasysh rastin $3x-5 \lt 0$:
Natyrisht, moduli do të hapet me një shenjë minus. Por atëherë lind një situatë e çuditshme: si në të majtë ashtu edhe në të djathtë në ekuacionin origjinal do të dalë e njëjta shprehje:
Pyes veten se në çfarë $x$ shprehja $5-3x$ do të jetë e barabartë me shprehjen $5-3x$? Edhe kapiteni Obviousness do të mbytej në pështymën e tij nga ekuacione të tilla, por ne e dimë: ky ekuacion është një identitet, d.m.th. është e vërtetë për çdo vlerë të ndryshores!
Kjo do të thotë se çdo $x$ do të na përshtatet. Megjithatë, ne kemi një kufizim:
Me fjalë të tjera, përgjigja nuk do të jetë një numër i vetëm, por një interval i tërë:
Së fundi, ka mbetur edhe një rast për t'u marrë parasysh: $3x-5=0$. Gjithçka është e thjeshtë këtu: nën modulin do të ketë zero, dhe moduli i zeros është gjithashtu i barabartë me zero (kjo rrjedh drejtpërdrejt nga përkufizimi):
Por pastaj ekuacioni origjinal $\left| 3x-5 \right|=5-3x$ do të rishkruhet si më poshtë:
Ne e kemi marrë tashmë këtë rrënjë më lart, kur kemi marrë parasysh rastin e $3x-5 \gt 0$. Për më tepër, kjo rrënjë është një zgjidhje për ekuacionin $3x-5=0$ - ky është kufizimi që ne vetë kemi prezantuar për të rivendosur modulin.
Kështu, përveç intervalit, do të jemi të kënaqur edhe me numrin që shtrihet në fund të këtij intervali:
 Kombinimi i rrënjëve në ekuacionet e modulit
Kombinimi i rrënjëve në ekuacionet e modulit Përgjigja përfundimtare totale: $x\in \left(-\infty ;\frac(5)(3) \djathtas]$ Nuk është shumë e zakonshme të shohësh një mut në përgjigjen e një ekuacioni mjaft të thjeshtë (në thelb linear) me modulin , Me të vërtetë, mësohu me të: vështirësia e modulit është se përgjigjet në ekuacione të tilla mund të jenë plotësisht të paparashikueshme.
Diçka tjetër është shumë më e rëndësishme: ne sapo kemi analizuar një algoritëm universal për zgjidhjen e një ekuacioni me një modul! Dhe ky algoritëm përbëhet nga hapat e mëposhtëm:
- Barazoni çdo modul në ekuacion me zero. Marrim disa ekuacione;
- Zgjidhini të gjitha këto ekuacione dhe shënoni rrënjët në vijën numerike. Si rezultat, vija e drejtë do të ndahet në disa intervale, në secilën prej të cilave të gjitha modulet zbulohen në mënyrë unike;
- Zgjidheni ekuacionin origjinal për çdo interval dhe kombinoni përgjigjet tuaja.
Kjo është ajo! Mbetet vetëm një pyetje: çfarë të bëjmë me rrënjët e marra në hapin 1? Le të themi se kemi dy rrënjë: $x=1$ dhe $x=5$. Ata do ta ndajnë vijën numerike në 3 pjesë:
 Ndarja e vijës numerike në intervale duke përdorur pika
Ndarja e vijës numerike në intervale duke përdorur pika Pra, cilat janë intervalet? Është e qartë se janë tre prej tyre:
- E majta: $x \lt 1$ — vetë njësia nuk përfshihet në interval;
- Qendrore: $1\le x \lt 5$ - këtu një përfshihet në interval, por pesë nuk përfshihen;
- E drejta: $x\ge 5$ - pesë përfshihen vetëm këtu!
Unë mendoj se ju tashmë e kuptoni modelin. Çdo interval përfshin skajin e majtë dhe nuk përfshin të djathtën.
Në pamje të parë, një hyrje e tillë mund të duket e papërshtatshme, e palogjikshme dhe në përgjithësi një lloj e çmendur. Por më besoni: pas një praktike të vogël, do të zbuloni se kjo qasje është më e besueshme dhe nuk ndërhyn në hapjen e paqartë të moduleve. Është më mirë të përdorësh një skemë të tillë sesa të mendosh çdo herë: jepni fundin majtas/djathtas në intervalin aktual ose "hedhe" atë në tjetrin.
Ruajtja e privatësisë suaj është e rëndësishme për ne. Për këtë arsye, ne kemi zhvilluar një politikë të privatësisë që përshkruan se si ne përdorim dhe ruajmë informacionin tuaj. Ju lutemi rishikoni praktikat tona të privatësisë dhe na tregoni nëse keni ndonjë pyetje.
Mbledhja dhe përdorimi i informacionit personal
Informacioni personal i referohet të dhënave që mund të përdoren për të identifikuar ose kontaktuar një person specifik.
Mund t'ju kërkohet të jepni informacionin tuaj personal në çdo kohë kur na kontaktoni.
Më poshtë janë disa shembuj të llojeve të informacionit personal që mund të mbledhim dhe se si mund ta përdorim këtë informacion.
Çfarë informacioni personal mbledhim:
- Kur dorëzoni një aplikim në sajt, ne mund të mbledhim informacione të ndryshme, duke përfshirë emrin tuaj, numrin e telefonit, adresën e emailit, etj.
Si i përdorim të dhënat tuaja personale:
- Informacioni personal që mbledhim na lejon t'ju kontaktojmë me oferta unike, promovime dhe ngjarje të tjera dhe ngjarje të ardhshme.
- Herë pas here, ne mund të përdorim të dhënat tuaja personale për të dërguar njoftime dhe komunikime të rëndësishme.
- Ne gjithashtu mund të përdorim të dhënat personale për qëllime të brendshme, si kryerja e auditimeve, analizave të të dhënave dhe kërkimeve të ndryshme, me qëllim që të përmirësojmë shërbimet që ofrojmë dhe t'ju ofrojmë rekomandime në lidhje me shërbimet tona.
- Nëse merrni pjesë në një tërheqje çmimesh, konkurs ose promovim të ngjashëm, ne mund të përdorim informacionin që ju jepni për të administruar programe të tilla.
Zbulimi i informacionit palëve të treta
Ne nuk ua zbulojmë informacionin e marrë nga ju palëve të treta.
Përjashtimet:
- Nëse është e nevojshme - në përputhje me ligjin, procedurën gjyqësore, në procedurat ligjore dhe/ose në bazë të kërkesave publike ose kërkesave nga organet qeveritare në Federatën Ruse - për të zbuluar informacionin tuaj personal. Ne gjithashtu mund të zbulojmë informacione për ju nëse përcaktojmë se një zbulim i tillë është i nevojshëm ose i përshtatshëm për qëllime sigurie, zbatimi të ligjit ose qëllime të tjera me rëndësi publike.
- Në rast të një riorganizimi, bashkimi ose shitjeje, ne mund t'i transferojmë informacionet personale që mbledhim te pala e tretë pasardhëse e aplikueshme.
Mbrojtja e informacionit personal
Ne marrim masa paraprake - duke përfshirë administrative, teknike dhe fizike - për të mbrojtur informacionin tuaj personal nga humbja, vjedhja dhe keqpërdorimi, si dhe qasja, zbulimi, ndryshimi dhe shkatërrimi i paautorizuar.
Respektimi i privatësisë suaj në nivel kompanie
Për t'u siguruar që informacioni juaj personal është i sigurt, ne i komunikojmë punonjësve tanë standardet e privatësisë dhe sigurisë dhe zbatojmë në mënyrë rigoroze praktikat e privatësisë.
Në këtë artikull do të shqyrtojmë në detaje moduli i numrit. Ne do të japim përkufizime të ndryshme të modulit të një numri, do të prezantojmë shënimin dhe do të ofrojmë ilustrime grafike. Në të njëjtën kohë, le të shohim shembuj të ndryshëm të gjetjes së modulit të një numri sipas përkufizimit. Pas kësaj, ne do të rendisim dhe justifikojmë vetitë kryesore të modulit. Në fund të artikullit, ne do të flasim se si përcaktohet dhe gjendet moduli i një numri kompleks.
Navigimi i faqes.
Moduli i numrave - përkufizimi, shënimi dhe shembuj
Fillimisht prezantojmë përcaktimi i modulit të numrit. Modulin e numrit a do ta shkruajmë si , pra majtas dhe djathtas numrit do të vendosim viza vertikale për të formuar shenjën e modulit. Le të japim disa shembuj. Për shembull, moduli −7 mund të shkruhet si ; moduli 4.125 shkruhet si dhe moduli ka një shënim të formës.
Përkufizimi i mëposhtëm i modulit i referohet , dhe për rrjedhojë , dhe numrave të plotë, dhe numrave racionalë dhe irracionalë, si pjesë përbërëse të grupit të numrave realë. Ne do të flasim për modulin e një numri kompleks në.
Përkufizimi.
Moduli i numrit a– ky është ose vetë numri a, nëse a është numër pozitiv, ose numri −a, e kundërta e numrit a, nëse a është numër negativ, ose 0, nëse a=0.
Përkufizimi i shprehur i modulit të një numri shpesh shkruhet në formën e mëposhtme  , kjo hyrje do të thotë se nëse a>0, nëse a=0, dhe nëse a<0
.
, kjo hyrje do të thotë se nëse a>0, nëse a=0, dhe nëse a<0
.
Regjistrimi mund të paraqitet në një formë më kompakte  . Ky shënim do të thotë se nëse (a është më e madhe ose e barabartë me 0), dhe nëse a<0
.
. Ky shënim do të thotë se nëse (a është më e madhe ose e barabartë me 0), dhe nëse a<0
.
Ekziston edhe hyrja  . Këtu duhet të shpjegojmë veçmas rastin kur a=0. Në këtë rast kemi , por −0=0, pasi zero konsiderohet një numër që është i kundërt me vetveten.
. Këtu duhet të shpjegojmë veçmas rastin kur a=0. Në këtë rast kemi , por −0=0, pasi zero konsiderohet një numër që është i kundërt me vetveten.
Le të japim shembuj të gjetjes së modulit të një numri duke përdorur përkufizimin e dhënë. Për shembull, le të gjejmë modulet e numrave 15 dhe . Le të fillojmë duke gjetur. Meqenëse numri 15 është pozitiv, moduli i tij, sipas përkufizimit, është i barabartë me vetë këtë numër, domethënë . Cili është moduli i një numri? Meqenëse është një numër negativ, moduli i tij është i barabartë me numrin e kundërt me numrin, domethënë numrin  . Kështu,.
. Kështu,.
Për të përfunduar këtë pikë, ne paraqesim një përfundim që është shumë i përshtatshëm për t'u përdorur në praktikë kur gjejmë modulin e një numri. Nga përkufizimi i modulit të një numri rezulton se moduli i një numri është i barabartë me numrin nën shenjën e modulit pa marrë parasysh shenjën e tij, dhe nga shembujt e diskutuar më sipër kjo është shumë qartë e dukshme. Deklarata e deklaruar shpjegon pse quhet edhe moduli i një numri vlera absolute e numrit. Pra, moduli i një numri dhe vlera absolute e një numri janë një dhe e njëjta.
Moduli i një numri si distancë
Gjeometrikisht, moduli i një numri mund të interpretohet si distancë. Le të japim përcaktimi i modulit të një numri në distancë.
Përkufizimi.
Moduli i numrit a– kjo është distanca nga origjina në vijën koordinative deri në pikën që i përgjigjet numrit a.
Ky përkufizim është në përputhje me përkufizimin e modulit të një numri të dhënë në paragrafin e parë. Le ta sqarojmë këtë pikë. Distanca nga origjina në pikën që i korrespondon një numri pozitiv është e barabartë me këtë numër. Zero korrespondon me origjinën, prandaj distanca nga origjina në pikën me koordinatë 0 është e barabartë me zero (nuk keni nevojë të lini mënjanë një segment të vetëm njësi dhe asnjë segment të vetëm që përbën ndonjë fraksion të një segmenti njësi në mënyrë për të arritur nga pika O në një pikë me koordinatë 0). Distanca nga origjina në një pikë me një koordinatë negative është e barabartë me numrin e kundërt të koordinatës së kësaj pike, pasi është e barabartë me distancën nga origjina në pikën koordinata e së cilës është numri i kundërt.
Për shembull, moduli i numrit 9 është i barabartë me 9, pasi distanca nga origjina në pikën me koordinatë 9 është e barabartë me nëntë. Le të japim një shembull tjetër. Pika me koordinatë −3.25 ndodhet në një distancë prej 3.25 nga pika O, pra ![]() .
.
Përkufizimi i deklaruar i modulit të një numri është një rast i veçantë i përcaktimit të modulit të ndryshimit të dy numrave.
Përkufizimi.
Moduli i ndryshimit të dy numrave a dhe b është e barabartë me distancën ndërmjet pikave të drejtëzës koordinative me koordinatat a dhe b.

Kjo do të thotë, nëse jepen pikat në vijën koordinative A(a) dhe B(b), atëherë distanca nga pika A në pikën B është e barabartë me modulin e ndryshimit midis numrave a dhe b. Nëse marrim pikën O (origjina) si pikën B, atëherë marrim përkufizimin e modulit të një numri të dhënë në fillim të këtij paragrafi.
Përcaktimi i modulit të një numri duke përdorur rrënjën katrore aritmetike
Herë pas here ndodh përcaktimi i modulit nëpërmjet rrënjës katrore aritmetike.
Për shembull, le të llogarisim modulin e numrave −30 dhe bazuar në këtë përkufizim. ne kemi. Në mënyrë të ngjashme, ne llogarisim modulin e dy të tretave:  .
.
Përkufizimi i modulit të një numri përmes rrënjës katrore aritmetike është gjithashtu në përputhje me përkufizimin e dhënë në paragrafin e parë të këtij neni. Le ta tregojmë. Le të jetë a një numër pozitiv dhe le të jetë −a një numër negativ. Pastaj ![]() Dhe
Dhe ![]() , nëse a=0 , atëherë
, nëse a=0 , atëherë ![]() .
.
Karakteristikat e modulit
Moduli ka një numër rezultatesh karakteristike - vetitë e modulit. Tani do të paraqesim kryesoret dhe më të përdorurat prej tyre. Kur justifikojmë këto veti, ne do të mbështetemi në përkufizimin e modulit të një numri për sa i përket distancës.
Le të fillojmë me vetinë më të dukshme të modulit - Moduli i një numri nuk mund të jetë një numër negativ. Në formë literale, kjo veti ka formën për çdo numër a. Kjo veti është shumë e lehtë për t'u justifikuar: moduli i një numri është një distancë, dhe distanca nuk mund të shprehet si një numër negativ.
Le të kalojmë te vetia e modulit tjetër. Moduli i një numri është zero nëse dhe vetëm nëse ky numër është zero. Moduli i zeros është zero sipas definicionit. Zero korrespondon me origjinën, asnjë pikë tjetër në vijën koordinative nuk korrespondon me zero, pasi çdo numër real shoqërohet me një pikë të vetme në vijën koordinative. Për të njëjtën arsye, çdo numër tjetër përveç zeros korrespondon me një pikë të ndryshme nga origjina. Dhe distanca nga origjina në çdo pikë tjetër përveç pikës O nuk është zero, pasi distanca midis dy pikave është zero nëse dhe vetëm nëse këto pika përkojnë. Arsyetimi i mësipërm vërteton se vetëm moduli i zeros është i barabartë me zero.
Le të vazhdojmë. Numrat e kundërt kanë module të barabarta, domethënë për çdo numër a. Në të vërtetë, dy pika në vijën koordinative, koordinatat e të cilave janë numra të kundërt, janë në të njëjtën distancë nga origjina, që do të thotë se modulet e numrave të kundërt janë të barabarta.
Vetia e mëposhtme e modulit është: Moduli i prodhimit të dy numrave është i barabartë me prodhimin e moduleve të këtyre numrave, domethënë, . Sipas përkufizimit, moduli i prodhimit të numrave a dhe b është i barabartë ose me a·b nëse , ose me −(a·b) nëse . Nga rregullat e shumëzimit të numrave real del se prodhimi i moduleve të numrave a dhe b është i barabartë ose me a·b, , ose me −(a·b) nëse , që vërteton vetinë në fjalë.
Moduli i herësit të një pjesëtuar me b është i barabartë me herësin e modulit të një numri të pjesëtuar me modulin e b, domethënë, . Le të justifikojmë këtë veti të modulit. Meqenëse herësi është i barabartë me produktin, atëherë. Në bazë të pasurisë së mëparshme që kemi  . Gjithçka që mbetet është të përdoret barazia , e cila është e vlefshme në bazë të përcaktimit të modulit të një numri.
. Gjithçka që mbetet është të përdoret barazia , e cila është e vlefshme në bazë të përcaktimit të modulit të një numri.
Vetia e mëposhtme e një moduli shkruhet si një pabarazi: ![]() , a , b dhe c janë numra realë arbitrarë. Pabarazia e shkruar nuk është gjë tjetër veçse pabarazia e trekëndëshit. Për ta bërë këtë të qartë, le të marrim pikat A(a), B(b), C(c) në vijën e koordinatave dhe të shqyrtojmë një trekëndësh të degjeneruar ABC, kulmet e të cilit shtrihen në të njëjtën drejtëz. Sipas definicionit, moduli i diferencës është i barabartë me gjatësinë e segmentit AB, - gjatësinë e segmentit AC dhe - gjatësinë e segmentit CB. Meqenëse gjatësia e njërës anë të trekëndëshit nuk e kalon shumën e gjatësive të dy brinjëve të tjera, atëherë pabarazia është e vërtetë
, a , b dhe c janë numra realë arbitrarë. Pabarazia e shkruar nuk është gjë tjetër veçse pabarazia e trekëndëshit. Për ta bërë këtë të qartë, le të marrim pikat A(a), B(b), C(c) në vijën e koordinatave dhe të shqyrtojmë një trekëndësh të degjeneruar ABC, kulmet e të cilit shtrihen në të njëjtën drejtëz. Sipas definicionit, moduli i diferencës është i barabartë me gjatësinë e segmentit AB, - gjatësinë e segmentit AC dhe - gjatësinë e segmentit CB. Meqenëse gjatësia e njërës anë të trekëndëshit nuk e kalon shumën e gjatësive të dy brinjëve të tjera, atëherë pabarazia është e vërtetë ![]() Prandaj, pabarazia është gjithashtu e vërtetë.
Prandaj, pabarazia është gjithashtu e vërtetë.
Pabarazia e sapo provuar është shumë më e zakonshme në formë ![]() . Pabarazia e shkruar zakonisht konsiderohet si një veti e veçantë e modulit me formulimin: " Moduli i shumës së dy numrave nuk e kalon shumën e moduleve të këtyre numrave" Por pabarazia vjen drejtpërdrejt nga mosbarazimi nëse vendosim −b në vend të b dhe marrim c=0.
. Pabarazia e shkruar zakonisht konsiderohet si një veti e veçantë e modulit me formulimin: " Moduli i shumës së dy numrave nuk e kalon shumën e moduleve të këtyre numrave" Por pabarazia vjen drejtpërdrejt nga mosbarazimi nëse vendosim −b në vend të b dhe marrim c=0.
Moduli i një numri kompleks
Le të japim përcaktimi i modulit të një numri kompleks. Të na jepet numër kompleks, i shkruar në formë algjebrike, ku x dhe y janë disa numra realë, që përfaqësojnë, përkatësisht, pjesët reale dhe imagjinare të një numri kompleks të dhënë z, dhe është njësia imagjinare.
Artikulli i mëparshëm: Sa është shpejtësia e dritës Artikulli vijues: Lëkundjet harmonike Formula e fizikës së frekuencës së lëkundjeve
