Pikat ekstreme të një funksioni. Cilat janë ekstremet e një funksioni: pikat kritike të maksimumit dhe minimumit

Duke kaluar në këto pabarazi në kufirin në Δ x→ 0 dhe duke marrë parasysh se derivati f "(x 0) ekziston, dhe për këtë arsye kufiri në të majtë nuk varet nga mënyra se si Δ x→ 0, marrim: në Δ x → 0 – 0 f"(x 0) ≥ 0 a në Δ x → 0 + 0 f"(x 0) ≤ 0. Meqenëse f"(x 0) përcakton një numër, atëherë këto dy pabarazi janë të pajtueshme vetëm nëse f"(x 0) = 0.

Teorema e provuar thotë se pikat maksimale dhe minimale mund të gjenden vetëm midis atyre vlerave të argumentit në të cilat derivati ​​bëhet zero.

Shqyrtuam rastin kur një funksion ka një derivat në të gjitha pikat e një segmenti të caktuar. Si është situata në rastet kur derivati ​​nuk ekziston? Le të shohim shembuj.

Shembuj.

1. y=|x|.

   Funksioni nuk ka derivat në pikë x=0 (në këtë pikë grafiku i funksionit nuk ka një tangjente të përcaktuar), por në këtë pikë funksioni ka një minimum, pasi y(0)=0, dhe për të gjitha x≠ 0y > 0.



Funksioni nuk ka derivat në x=0, pasi shkon në pafundësi në x=0. Por në këtë pikë funksioni ka një maksimum.



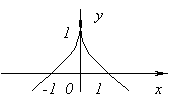
Funksioni nuk ka derivat në x=0, pasi në x→0. Në këtë pikë funksioni nuk ka as një maksimum dhe as një minimum. Vërtet, f(x)=0 dhe në x<0f(x)<0, а при x>0f(x)>0.



Kështu, nga shembujt e dhënë dhe nga teorema e formuluar del qartë se një funksion mund të ketë një ekstrem vetëm në dy raste: 1) në pikat ku derivati ​​ekziston dhe është i barabartë me zero; 2) në pikën ku derivati ​​nuk ekziston.

Megjithatë, nëse në një moment x 0 ne e dimë këtë f" (x 0 ) =0, atëherë nuk mund të konkludohet nga kjo se në pikën x 0 funksioni ka një ekstrem.

Për shembull. .



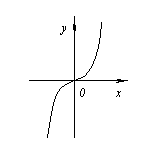
Por periudha x=0 nuk është një pikë ekstreme, pasi në të majtë të kësaj pike vlerat e funksionit janë të vendosura poshtë boshtit kau, dhe në të djathtë sipër.

Quhen vlerat e një argumenti nga fusha e një funksioni në të cilin derivati ​​i funksionit zhduket ose nuk ekziston. pikat kritike.




Nga të gjitha sa më sipër, rezulton se pikat ekstreme të funksionit janë ndër pikat kritike, dhe, megjithatë, jo çdo pikë kritike është një pikë ekstreme. Prandaj, për të gjetur ekstremin e një funksioni, duhet të gjeni të gjitha pikat kritike të funksionit dhe më pas të ekzaminoni secilën prej këtyre pikave veçmas për maksimumin dhe minimumin. Teorema e mëposhtme i shërben këtij qëllimi.

Teorema 2. (Kusht i mjaftueshëm për ekzistencën e një ekstremi.) Le të jetë funksioni i vazhdueshëm në një interval që përmban pikën kritike x 0, dhe është i diferencueshëm në të gjitha pikat e këtij intervali (përveç, ndoshta, vetë pikës x 0). Nëse, kur lëviz nga e majta në të djathtë përmes kësaj pike, derivati ​​ndryshon shenjën nga plus në minus, atëherë në pikën x = x Funksioni 0 ka një maksimum. Nëse, kur kaloni x 0 nga e majta në të djathtë, derivati ​​ndryshon shenjën nga minus në plus, atëherë funksioni ka një minimum në këtë pikë.

Kështu, nëse

Dëshmi. Së pari, le të supozojmë se kur kalojmë x 0 derivati ​​ndryshon shenjën nga plus në minus, d.m.th. para të gjithëve x, afër pikës x 0 f "(x)> 0 për x< x 0 , f" (x)< 0 për x>x 0 . Le të zbatojmë teoremën e Lagranzhit për diferencën f(x) - f(x 0 ) = f "(c) (x- x 0), ku c shtrihet mes x Dhe x 0 .

1. Le x< x 0 . Pastaj c< x 0 dhe f "(c)> 0. Kjo është arsyeja pse f "(c) (x- x 0)< 0 dhe prandaj

   f(x) - f(x 0 )< 0, d.m.th. f(x)< f(x 0 ).

2. Le x > x 0 . Pastaj c>x 0 dhe f" (c)< 0. Mjetet f "(c) (x- x 0)< 0. Kjo është arsyeja pse f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Kështu, për të gjitha vlerat x mjaft afër x 0 f(x)< f(x 0 ) . Dhe kjo do të thotë se në pikën x Funksioni 0 ka një maksimum.

Pjesa e dytë e teoremës minimale vërtetohet në mënyrë të ngjashme.



Le të ilustrojmë kuptimin e kësaj teoreme në figurë. Le f" (x 1 ) =0 dhe për cilindo x, mjaft afër x 1, pabarazitë janë të kënaqura

f" (x)< 0 në x< x 1 , f "(x)> 0 në x>x 1 .

Pastaj në të majtë të pikës x 1 funksioni rritet dhe zvogëlohet në të djathtë, pra, kur x = x 1 funksion shkon nga rritja në zvogëlim, domethënë ka një maksimum.

Në mënyrë të ngjashme, ne mund të shqyrtojmë pikat x 2 dhe x 3 .


Të gjitha sa më sipër mund të përshkruhen skematikisht në foto:

Rregulla për studimin e funksionit y=f(x) për ekstremin

1. Gjeni domenin e një funksioni f(x).
2. Gjeni derivatin e parë të një funksioni f" (x).
3. Përcaktoni pikat kritike për këtë:
   1. gjeni rrënjët reale të ekuacionit f" (x)=0;
   2. gjeni të gjitha vlerat x për të cilat derivati f" (x) nuk ekziston.
4. Përcaktoni shenjën e derivatit majtas dhe djathtas të pikës kritike. Meqenëse shenja e derivatit mbetet konstante ndërmjet dy pikave kritike, mjafton të përcaktohet shenja e derivatit në një pikë në të majtë dhe një pikë në të djathtë të pikës kritike.
5. Llogaritni vlerën e funksionit në pikat ekstreme.

Shembuj. Eksploroni funksionet për minimumin dhe maksimumin.




VLERA MAKSIMALE DHE MË E VOGLA E NJË FUNKSIONI NË NJË Segment

Më i madhi vlera e një funksioni në një interval është më e madhja nga të gjitha vlerat e tij në këtë interval, dhe më i vogli– më e vogla nga të gjitha vlerat e saj.

Merrni parasysh funksionin y=f(x) e vazhdueshme në segmentin [ a, b]. Siç dihet, një funksion i tillë arrin vlerat e tij maksimale dhe minimale, qoftë në kufirin e segmentit ose brenda tij. Nëse vlera më e madhe ose më e vogël e një funksioni arrihet në një pikë të brendshme të segmentit, atëherë kjo vlerë është maksimumi ose minimumi i funksionit, domethënë arrihet në pikat kritike.

Kështu, marrim sa vijon rregull për gjetjen e vlerave më të mëdha dhe më të vogla të një funksioni në një segment a, b] :

1. Gjeni të gjitha pikat kritike të funksionit në intervalin ( a, b) dhe llogaritni vlerat e funksionit në këto pika.
2. Llogaritni vlerat e funksionit në skajet e segmentit kur x = a, x = b.
3. Nga të gjitha vlerat e marra, zgjidhni më të madhin dhe më të voglin.

Gjeni vlerën më të madhe të funksionit y=(7x^2-56x+56)e^x në segmentin [-3; 2].

Zgjidhje

Le të gjejmë derivatin e funksionit origjinal duke përdorur formulën e derivatit të produktit y"=(7x^2-56x+56)"e^x\,+ (7x^2-56x+56)\majtas(e^x\djathtas)"= (14x-56)e^x+(7x^2-56x+56)e^x= (7x^2-42x)e^x= 7x(x-6)e^x. Le të llogarisim zerot e derivatit: y"=0;

7x(x-6)e^x=0,

x_1=0, x_2=6.

Le të rregullojmë shenjat e derivatit dhe të përcaktojmë intervalet e monotonitetit të funksionit origjinal në një segment të caktuar.

Nga figura duket qartë se në segmentin [-3; 0] funksioni origjinal rritet, dhe në segment zvogëlohet. Kështu, vlera më e madhe në segment [-3; 2] arrihet në x=0 dhe është e barabartë me y(0)= 7\cdot 0^2-56\cdot 0+56=56.

Përgjigju

gjendja

Gjeni vlerën më të madhe të funksionit y=12x-12tg x-18 në segment \majtas.

Zgjidhje

y"= (12x)"-12(tg x)"-(18)"= 12-\frac(12)(\cos ^2x)= \frac(12\cos ^2x-12)(\cos ^2x)\leqslant0. Kjo do të thotë që funksioni origjinal nuk është në rritje në intervalin në shqyrtim dhe merr vlerën më të madhe në skajin e majtë të intervalit, pra në x=0. y(0)= Vlera më e madhe është -18.

Përgjigju

12\cdot 0-12 tg (0)-18=

gjendja

Burimi: “Matematika. Përgatitja për Provimin e Unifikuar të Shtetit 2017. Niveli i profilit." Ed. F. F. Lysenko, S. Yu.

Zgjidhje

Gjeni pikën minimale të funksionit y=(x+8)^2e^(x+52).

Ne do të gjejmë pikën minimale të funksionit duke përdorur derivatin. Le të gjejmë derivatin e një funksioni të caktuar duke përdorur formulat për derivatin e produktit, derivatin e x^\alfa dhe e^x: y"(x)= \left((x+8)^2\djathtas)"e^(x+52)+(x+8)^2\left(e^(x+52)\djathtas)"= 2(x+8)e^(x+52)+(x+8)^2e^(x+52)= (x+8)e^(x+52)(2+x+8)=

(x+8)(x+10)e^(x+52). Le të renditim shenjat e derivatit dhe të përcaktojmë intervalet e monotonitetit të funksionit origjinal. e^(x+52)>0 për çdo x. y"=0 në x=-8,

x=-10.

Përgjigju

12\cdot 0-12 tg (0)-18=

gjendja

Figura tregon se funksioni y=(x+8)^2e^(x+52) ka një pikë minimale të vetme x=-8. Gjeni pikën maksimale të funksionit

Zgjidhje

y=8x-\frac23x^\tfrac32-106.

ODZ: x \geqslant 0. Le të gjejmë derivatin e funksionit origjinal:

y"=8-\frac23\cdot\frac32x^\tfrac12=8-\sqrt x.

Le të llogarisim zerot e derivatit:

8-\sqrt x=0;

\sqrt x=8;

x=64.

Le të renditim shenjat e derivatit dhe të përcaktojmë intervalet e monotonitetit të funksionit origjinal.

Përgjigju

12\cdot 0-12 tg (0)-18=

gjendja

Figura tregon se pika x=64 është e vetmja pikë maksimale e funksionit të dhënë. Gjeni vlerën më të vogël të funksionit y=5x^2-12x+2\n x+37 në segment

Zgjidhje

\left[\frac35; \frac75\djathtas].

ODZ: x>0.

Ne do të gjejmë pikën minimale të funksionit duke përdorur derivatin. Le të gjejmë derivatin e një funksioni të caktuar duke përdorur formulat për derivatin e produktit, derivatin e x^\alfa dhe e^x: Le të gjejmë derivatin e funksionit origjinal: 10x-12+\frac(2)(x)=

\frac(10x^2-12x+2)(x).

Le të përcaktojmë zerot e derivatit: y"(x)=0;

\frac(10x^2-12x+2)(x)=0,

5x^2-6x+1=0, x_(1,2)= \frac(3\pm\sqrt(3^2-5\cdot1))(5)=

\frac(3\pm2)(5),

x_1=\frac15\notin\majtas[\frac35; \frac75\djathtas],

x_2=1\në\majtas[\frac35; \frac75\djathtas].

Le të rregullojmë shenjat e derivatit dhe të përcaktojmë intervalet e monotonitetit të funksionit origjinal në intervalin në shqyrtim. Nga figura duket qartë se në segment\left[\frac35; 1\djathtas] funksioni origjinal zvogëlohet, dhe në segment rritet. Kështu, vlera më e vogël në segment \left[\frac35; \frac75\djathtas] arrihet në x=1 dhe është e barabartë me y(1)= 5\cdot 1^2-12\cdot 1+2 \ln 1+37= 30.

Përgjigju

12\cdot 0-12 tg (0)-18=

gjendja

Gjeni vlerën më të madhe të funksionit y=(x+4)^2(x+1)+19 në segmentin [-5; -3].

Zgjidhje

Le të gjejmë derivatin e funksionit origjinal duke përdorur formulën e derivatit të produktit.

Siç mund ta shihni, kjo shenjë e një ekstremi të një funksioni kërkon ekzistencën e një derivati ​​të paktën në rendin e dytë në pikë.

Shembull.

Gjeni ekstremin e funksionit.

Zgjidhje.

Le të fillojmë me fushën e përkufizimit:

Le të dallojmë funksionin origjinal:

x=1, domethënë kjo është një pikë e ekstremit të mundshëm. Gjejmë derivatin e dytë të funksionit dhe llogarisim vlerën e tij në:

x = 1 x=1 Prandaj, me kushtin e dytë të mjaftueshëm për një ekstrem, - pikë maksimale. Pastaj

- funksioni maksimal.

Ilustrim grafik.

Përgjigje:

Kushti i tretë i mjaftueshëm për ekstremin e një funksioni. y=f(x) Lëreni funksionin ka derivate deri në n -rendi i -te fqinjesise se pikes dhe derivateve deri n+1

Shembull.

-rendit në vetë pikën. Le të jetë. .

Zgjidhje.

Gjeni pikat ekstreme të funksionit

Funksioni origjinal është një funksion i tërë racional;

Le të dallojmë funksionin: Derivati ​​shkon në zero në

Prandaj, këto janë pika të ekstremit të mundshëm. Le të përdorim kushtin e tretë të mjaftueshëm për një ekstrem.

Ne gjejmë derivatin e dytë dhe llogarisim vlerën e tij në pikat e ekstremit të mundshëm (do të heqim llogaritjet e ndërmjetme): Rrjedhimisht, është pika maksimale (për shenjën e tretë të mjaftueshme të ekstremit që kemi n=1

Dhe). Për të zbuluar natyrën e pikave

gjejmë derivatin e tretë dhe llogarisim vlerën e tij në këto pika: Prandaj, a është pika e lakimit të funksionit ( n=1

n=2

Mbetet të merremi me çështjen. Gjejmë derivatin e katërt dhe llogarisim vlerën e tij në këtë pikë:

- funksioni maksimal.

Ilustrim grafik.

Prandaj, është pika minimale e funksionit.

Pika maksimale është pika minimale e funksionit.

10. Ekstrema e një funksioni Përkufizimi i një ekstremi Thirret funksioni y = f(x). (në rritje në rënie< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >) në një interval të caktuar, nëse për x 1

f (x 2)).

Nëse funksioni i diferencueshëm y = f(x) rritet (zvogëlohet) në një interval, atëherë derivati ​​i tij në këtë interval f " (x)  0

(f " (x)  0). x Pika O thirrur (pikë maksimale lokale minimale x Pika) funksioni f(x), nëse ka një fqinjësi të pikës

, për të gjitha pikat e të cilave mosbarazimi f(x) ≤ f(x о) (f(x) ≥ f(x о)) është i vërtetë. Quhen pikët maksimale dhe minimale pika ekstreme , dhe vlerat e funksionit në këto pika janë të tij

ekstremet.

Pikat ekstreme Kushtet e nevojshme për një ekstrem x Pikaështë një pikë ekstreme e funksionit f(x), atëherë ose f " (x o) = 0, ose f (x o) nuk ekziston. Pika të tilla quhen kritike, dhe vetë funksioni përcaktohet në pikën kritike. Ekstrema e një funksioni duhet kërkuar ndër pikat e tij kritike.

Kushti i parë i mjaftueshëm. Le x Pika- pika kritike. Nëse f "(x) kur kalon nëpër një pikë x Pika ndryshon shenjën plus në minus, pastaj në pikë x Pika funksioni ka një maksimum, përndryshe ka një minimum. Nëse, gjatë kalimit nëpër pikën kritike, derivati ​​nuk ndryshon shenjë, atëherë në pikën x Pika nuk ka ekstrem.

Kushti i dytë i mjaftueshëm. Le të ketë funksioni f(x) një derivat f " (x) në afërsi të pikës x Pika dhe derivati ​​i dytë në vetë pikën x Pika. Nëse f "(x o) = 0, >0 (<0), то точка x Pikaështë pika minimale (maksimale) lokale e funksionit f(x). Nëse =0, atëherë duhet të përdorni kushtin e parë të mjaftueshëm ose të përdorni derivate më të lartë.

Në një segment, funksioni y = f(x) mund të arrijë vlerën e tij minimale ose maksimale qoftë në pikat kritike ose në skajet e segmentit.

Shembulli 3.22. Gjeni ekstremin e funksionit f(x) = 2x 3 - 15x 2 + 36x - 14.

Zgjidhje. Meqenëse f "(x) = 6x 2 - 30x +36 = 6(x‑2)(x - 3), atëherë pikat kritike të funksionit x 1 = 2 dhe x 2 = 3. Ekstrema mund të jetë vetëm në Pra, kur kalon në pikën x 1 = 2, derivati ​​ndryshon shenjën e tij nga plus në minus, atëherë në këtë pikë funksioni ka një maksimum kur kalon në pikën x 2 = 3 në plus, pra në pikën x 2 = 3 funksioni ka një minimum, pasi kemi llogaritur vlerat e funksionit në pikat x 1 = 2 dhe x 2 = 3, gjejmë ekstremin e funksionit: maksimumi f(. 2) = 14 dhe minimumi f(3) = 13.

Para se të mësoni se si të gjeni ekstremet e një funksioni, duhet të kuptoni se çfarë është një ekstrem. Përkufizimi më i përgjithshëm i një ekstremi është se ai është, siç përdoret në matematikë, vlera më e vogël ose më e madhe e një funksioni në një grup të caktuar të një rreshti numerik ose grafik. Në vendin ku ndodhet minimumi shfaqet ekstremi minimal dhe aty ku ndodhet maksimumi shfaqet ekstremi maksimal. Gjithashtu në një disiplinë të tillë si analiza matematikore, identifikohen ekstremet lokale të një funksioni. Tani le të shohim se si të gjejmë pikat ekstreme.

Ekstremet në matematikë janë ndër karakteristikat më të rëndësishme të një funksioni, ato tregojnë vlerat më të mëdha dhe më të vogla të tij. Ekstremat gjenden kryesisht në pikat kritike të funksioneve që gjenden. Vlen të përmendet se është në pikën ekstreme që funksioni ndryshon rrënjësisht drejtimin e tij. Nëse llogaritni derivatin e pikës ekstreme, atëherë, sipas përkufizimit, ai duhet të jetë i barabartë me zero ose do të mungojë plotësisht. Kështu, për të zbuluar se si të gjeni ekstremin e një funksioni, duhet të kryeni dy detyra vijuese:

• gjeni derivatin për funksionin që duhet të përcaktohet nga detyra;
• gjeni rrënjët e ekuacionit.

Sekuenca e gjetjes së ekstremit

1. Shkruani funksionin f(x) që është dhënë. Gjeni derivatin e tij të rendit të parë f "(x). Barazoni shprehjen që rezulton me zero.
2. Tani ju duhet të zgjidhni ekuacionin që rezulton. Zgjidhjet që rezultojnë do të jenë rrënjët e ekuacionit, si dhe pikat kritike të funksionit që përcaktohet.
3. Tani përcaktojmë se cilat pika kritike (maksimale ose minimale) janë rrënjët e gjetura. Hapi tjetër, pasi të kemi mësuar se si të gjejmë pikat ekstreme të një funksioni, është të gjejmë derivatin e dytë të funksionit të dëshiruar f "(x). Do të jetë e nevojshme të zëvendësohen vlerat e pikave kritike të gjetura në një pabarazi specifike dhe më pas llogarisni çfarë ndodh nëse kjo ndodh, nëse derivati ​​i dytë rezulton të jetë më i madh se zero në pikën kritike, atëherë ajo do të jetë pika minimale, dhe përndryshe ajo do të jetë pika maksimale.
4. Mbetet për të llogaritur vlerën e funksionit fillestar në pikat maksimale dhe minimale të kërkuara të funksionit. Për ta bërë këtë, ne zëvendësojmë vlerat e marra në funksion dhe llogarisim. Sidoqoftë, vlen të përmendet se nëse pika kritike rezulton të jetë një maksimum, atëherë ekstremi do të jetë maksimal, dhe nëse është një minimum, atëherë do të jetë minimal për analogji.

Algoritmi për gjetjen e ekstremit

Për të përmbledhur njohuritë e marra, ne do të krijojmë një algoritëm të shkurtër se si të gjejmë pikat ekstreme.

1. Gjejmë domenin e përkufizimit të një funksioni të caktuar dhe intervalet e tij, të cilat përcaktojnë saktësisht se në cilat intervale funksioni është i vazhdueshëm.
2. Gjeni derivatin e funksionit f "(x).
3. Llogaritim pikat kritike të ekuacionit y = f (x).
4. Ne analizojmë ndryshimet në drejtimin e funksionit f (x), si dhe shenjën e derivatit f "(x) ku pikat kritike ndajnë domenin e përcaktimit të këtij funksioni.
5. Tani përcaktojmë nëse çdo pikë në grafik është maksimumi apo minimumi.
6. Vlerat e funksionit i gjejmë në ato pika që janë ekstreme.
7. Ne regjistrojmë rezultatin e këtij studimi - ekstremet dhe intervalet e monotonitetit. Kjo është e gjitha. Tani ne kemi parë se si mund të gjeni një ekstrem në çdo interval. Nëse keni nevojë të gjeni një ekstrem në një interval të caktuar të një funksioni, atëherë kjo bëhet në mënyrë të ngjashme, duhet të merren parasysh vetëm kufijtë e kërkimit që kryhet.

Pra, ne shikuam se si të gjejmë pikat ekstreme të një funksioni. Me ndihmën e llogaritjeve të thjeshta, si dhe njohurive për gjetjen e derivateve, mund të gjeni çdo ekstrem dhe ta llogaritni atë, si dhe ta tregoni grafikisht. Gjetja e ekstremeve është një nga seksionet më të rëndësishme të matematikës, si në shkollë ashtu edhe në arsimin e lartë, prandaj, nëse mësoni t'i identifikoni saktë ato, atëherë studimi do të bëhet shumë më i lehtë dhe më interesant.

Për të përcaktuar natyrën e një funksioni dhe për të folur për sjelljen e tij, është e nevojshme të gjenden intervalet e rritjes dhe uljes. Ky proces quhet hulumtimi i funksionit dhe grafiku. Pika ekstreme përdoret kur gjenden vlerat më të mëdha dhe më të vogla të një funksioni, pasi në to funksioni rritet ose zvogëlohet nga intervali.

Ky artikull zbulon përkufizimet, formulon një shenjë të mjaftueshme të rritjes dhe uljes së intervalit dhe një kusht për ekzistencën e një ekstremi. Kjo vlen për zgjidhjen e shembujve dhe problemeve. Seksioni për funksionet diferencuese duhet të përsëritet, sepse zgjidhja do të duhet të përdorë gjetjen e derivatit.

Yandex.RTB R-A-339285-1 Përkufizimi 1

Funksioni y = f (x) do të rritet në intervalin x kur, për çdo x 1 ∈ X dhe x 2 ∈ X, x 2 > x 1, pabarazia f (x 2) > f (x 1) plotësohet. Me fjalë të tjera, një vlerë më e madhe e argumentit korrespondon me një vlerë më të madhe të funksionit.

Përkufizimi 2

Funksioni y = f (x) konsiderohet të jetë në rënie në intervalin x kur, për çdo x 1 ∈ X, x 2 ∈ X, x 2 > x 1, barazia f (x 2) > f (x 1) konsiderohet e vërtetë. Me fjalë të tjera, një vlerë më e madhe funksioni korrespondon me një vlerë më të vogël të argumentit. Konsideroni figurën më poshtë.

Koment: Kur funksioni është i caktuar dhe i vazhdueshëm në skajet e intervalit të rritjes dhe zvogëlimit, domethënë (a; b), ku x = a, x = b, pikat përfshihen në intervalin e rritjes dhe zvogëlimit. Kjo nuk bie ndesh me përkufizimin, do të thotë se ndodh në intervalin x.

Vetitë kryesore të funksioneve elementare të tipit y = sin x janë siguria dhe vazhdimësia për vlerat reale të argumenteve. Nga këtu marrim se sinusi rritet gjatë intervalit - π 2; π 2, atëherë rritja në segment ka formën - π 2; π 2.

Pika x 0 quhet pikë maksimale për funksionin y = f (x), kur për të gjitha vlerat e x është i vlefshëm pabarazia f (x 0) ≥ f (x). Funksioni maksimalështë vlera e funksionit në një pikë dhe shënohet me y m a x.

Pika x 0 quhet pika minimale për funksionin y = f (x), kur për të gjitha vlerat e x është e vlefshme pabarazia f (x 0) ≤ f (x). Funksionet minimaleështë vlera e funksionit në një pikë dhe ka një emërtim të formës y m i n.

Konsiderohen lagjet e pikës x 0 pikat ekstreme, dhe vlera e funksionit që korrespondon me pikat ekstreme. Konsideroni figurën më poshtë.

Ekstrema e një funksioni me vlerën më të madhe dhe më të vogël të funksionit. Konsideroni figurën më poshtë.

Figura e parë thotë se është e nevojshme të gjendet vlera më e madhe e funksionit nga segmenti [a; b]. Gjendet duke përdorur pikat maksimale dhe është e barabartë me vlerën maksimale të funksionit, dhe figura e dytë është më shumë si gjetja e pikës maksimale në x = b.

Kushtet e mjaftueshme që një funksion të rritet dhe ulet

Për të gjetur maksimumin dhe minimumin e një funksioni, është e nevojshme të aplikohen shenjat e ekstremit në rastin kur funksioni i plotëson këto kushte. Shenja e parë konsiderohet më e përdorura.

Kushti i parë i mjaftueshëm për një ekstrem

Le të jepet një funksion y = f (x), i cili është i diferencueshëm në një lagje ε të pikës x 0 dhe ka vazhdimësi në pikën e dhënë x 0. Nga këtu ne e marrim atë

• kur f " (x) > 0 me x ∈ (x 0 - ε ; x 0) dhe f " (x)< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• kur f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 për x ∈ (x 0 ; x 0 + ε), atëherë x 0 është pika minimale.

Me fjalë të tjera, marrim kushtet e tyre për vendosjen e shenjës:

• kur funksioni është i vazhdueshëm në pikën x 0, atëherë ai ka një derivat me shenjë ndryshimi, domethënë nga + në -, që do të thotë se pika quhet maksimum;
• kur funksioni është i vazhdueshëm në pikën x 0, atëherë ai ka një derivat me shenjë ndryshimi nga - në +, që do të thotë se pika quhet minimale.

Për të përcaktuar saktë pikat maksimale dhe minimale të një funksioni, duhet të ndiqni algoritmin për gjetjen e tyre:

• gjeni domenin e përkufizimit;
• gjeni derivatin e funksionit në këtë zonë;
• të identifikojë zero dhe pika ku funksioni nuk ekziston;
• përcaktimi i shenjës së derivatit në intervale;
• zgjidhni pikat ku funksioni ndryshon shenjën.

Le të shqyrtojmë algoritmin duke zgjidhur disa shembuj të gjetjes së ekstremeve të një funksioni.

Shembulli 1

Gjeni pikat maksimale dhe minimale të funksionit të dhënë y = 2 (x + 1) 2 x - 2 .

Zgjidhje

Fusha e përkufizimit të këtij funksioni janë të gjithë numrat realë përveç x = 2. Së pari, le të gjejmë derivatin e funksionit dhe të marrim:

y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2 ) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Nga këtu shohim se zerot e funksionit janë x = - 1, x = 5, x = 2, domethënë secila kllapa duhet të barazohet me zero. Le ta shënojmë në boshtin e numrave dhe të marrim:

Tani përcaktojmë shenjat e derivatit nga çdo interval. Është e nevojshme të zgjidhni një pikë të përfshirë në interval dhe ta zëvendësoni atë në shprehje. Për shembull, pikat x = - 2, x = 0, x = 3, x = 6.

Ne e kuptojmë atë

y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, që do të thotë se intervali - ∞ - 1 ka një derivat pozitiv në mënyrë të ngjashme.

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Meqenëse intervali i dytë doli të jetë më i vogël se zero, do të thotë që derivati ​​në interval do të jetë negativ. E treta me një minus, e katërta me një plus. Për të përcaktuar vazhdimësinë, duhet t'i kushtoni vëmendje shenjës së derivatit nëse ndryshon, atëherë kjo është një pikë ekstreme.

Gjejmë se në pikën x = - 1 funksioni do të jetë i vazhdueshëm, që do të thotë se derivati ​​do të ndryshojë shenjën nga + në -. Sipas shenjës së parë, ne kemi se x = - 1 është një pikë maksimale, që do të thotë se marrim

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

Pika x = 5 tregon se funksioni është i vazhdueshëm dhe derivati ​​do të ndryshojë shenjën nga – në +. Kjo do të thotë se x = -1 është pika minimale, dhe përcaktimi i saj ka formën

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Imazhi grafik

Ilustrim grafik. y m a x = y (- 1) = 0, y m i n = y (5) = 24.

Vlen t'i kushtohet vëmendje faktit që përdorimi i kriterit të parë të mjaftueshëm për një ekstrem nuk kërkon që funksioni të jetë i diferencueshëm në pikën x 0, gjë që thjeshton llogaritjen.

Shembulli 2

Gjeni pikat maksimale dhe minimale të funksionit y = 1 6 x 3 = 2 x 2 + 22 3 x - 8.

Zgjidhje.

Fusha e një funksioni janë të gjithë numrat realë. Kjo mund të shkruhet si një sistem ekuacionesh të formës:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Pastaj ju duhet të gjeni derivatin:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

Pika x = 0 nuk ka një derivat, sepse vlerat e kufijve të njëanshëm janë të ndryshme. Ne marrim se:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

Nga kjo rrjedh se funksioni është i vazhdueshëm në pikën x = 0, atëherë ne llogarisim

lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

Është e nevojshme të kryhen llogaritjet për të gjetur vlerën e argumentit kur derivati ​​bëhet zero:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

Të gjitha pikat e marra duhet të shënohen në një vijë të drejtë për të përcaktuar shenjën e çdo intervali. Prandaj, është e nevojshme të llogaritet derivati ​​në pika arbitrare për çdo interval. Për shembull, mund të marrim pikë me vlera x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6. Ne e kuptojmë atë

y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Imazhi në vijën e drejtë duket si

Kjo do të thotë se arrijmë në përfundimin se është e nevojshme t'i drejtohemi shenjës së parë të një ekstremi. Le ta llogarisim dhe ta gjejmë atë

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , pastaj nga këtu pikët maksimale kanë vlerat x = - 4 + 2 3 3 , x = 4 - 2 3 3

Le të kalojmë në llogaritjen e minimumeve:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Le të llogarisim maksimumin e funksionit. Ne e kuptojmë atë

y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Imazhi grafik

Ilustrim grafik.

y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 m 27 x3 = y 4 - 2 3 3 = 8 27 3

Nëse është dhënë një funksion f "(x 0) = 0, atëherë nëse f "" (x 0) > 0, marrim se x 0 është një pikë minimale nëse f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

Shembulli 3

Gjeni maksimumin dhe minimumin e funksionit y = 8 x x + 1.

Zgjidhje

Së pari, gjejmë domenin e përkufizimit. Ne e kuptojmë atë

D(y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Është e nevojshme të diferencojmë funksionin, pas së cilës marrim

y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

Në x = 1, derivati ​​bëhet zero, që do të thotë se pika është një ekstrem i mundshëm. Për të sqaruar, është e nevojshme të gjendet derivati ​​i dytë dhe të llogaritet vlera në x = 1. Ne marrim:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2 "x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0

Kjo do të thotë që duke përdorur kushtin 2 të mjaftueshëm për një ekstrem, marrim se x = 1 është një pikë maksimale. Përndryshe, hyrja duket si y m a x = y (1) = 8 1 1 + 1 = 4.

Imazhi grafik

Ilustrim grafik. y m a x = y (1) = 4 ..

Funksioni y = f (x) ka derivatin e tij deri në rendin e n-të në lagjen ε të një pike të dhënë x 0 dhe derivatin e tij deri në rendin n + 1 në pikën x 0 . Pastaj f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Nga kjo rrjedh se kur n është një numër çift, atëherë x 0 konsiderohet një pikë lakimi, kur n është një numër tek, atëherë x 0 është një pikë ekstreme dhe f (n + 1) (x 0) > 0, atëherë x 0 është një pikë minimale, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.

Shembulli 4

Gjeni pikat maksimale dhe minimale të funksionit y y = 1 16 (x + 1) 3 (x - 3) 4.

Zgjidhje

Funksioni origjinal është një funksion i tërë racional, që do të thotë se domeni i përkufizimit janë të gjithë numrat realë. Është e nevojshme të diferencohet funksioni. Ne e kuptojmë atë

y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Ky derivat do të shkojë në zero në x 1 = - 1, x 2 = 5 7, x 3 = 3. Kjo do të thotë, pikat mund të jenë pika ekstreme të mundshme. Është e nevojshme të zbatohet kushti i tretë i mjaftueshëm për ekstremin. Gjetja e derivatit të dytë ju lejon të përcaktoni me saktësi praninë e një maksimumi dhe minimumi të një funksioni. Derivati ​​i dytë llogaritet në pikat e ekstremumit të tij të mundshëm. Ne e kuptojmë atë

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

Kjo do të thotë se x 2 = 5 7 është pika maksimale. Duke zbatuar kriterin e tretë të mjaftueshëm, gjejmë se për n = 1 dhe f (n + 1) 5 7< 0 .

Është e nevojshme të përcaktohet natyra e pikave x 1 = - 1, x 3 = 3. Për ta bërë këtë, ju duhet të gjeni derivatin e tretë dhe të llogaritni vlerat në këto pika. Ne e kuptojmë atë

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Kjo do të thotë se x 1 = - 1 është pika e lakimit të funksionit, pasi për n = 2 dhe f (n + 1) (- 1) ≠ 0. Është e nevojshme të hulumtohet pika x 3 = 3. Për ta bërë këtë, gjejmë derivatin e 4-të dhe kryejmë llogaritjet në këtë pikë:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

Nga sa u vendos më sipër, arrijmë në përfundimin se x 3 = 3 është pika minimale e funksionit.

Imazhi grafik

Ilustrim grafik. x 2 = 5 7 është pika maksimale, x 3 = 3 është pika minimale e funksionit të dhënë.

Nëse vëreni një gabim në tekst, ju lutemi theksoni atë dhe shtypni Ctrl+Enter