Az óra céljai:

Fejleszteni kell ismereteket, készségeket és képességeket az intervallumok általánosított módszerének hatékony használatához, a folytonos függvények tulajdonságai alapján;

Fogalmazzon meg egy algoritmust az ekvivalens transzformációhoz vezető műveletekből;

Tanítsa meg önállóan alkalmazni az egyenlőtlenségek megoldása során;

A tudás, készségek és képességek átadása új körülmények között.

Oktatási: ismeretek, készségek, képességek rendszerezése, megszilárdítása, általánosítása.

Nevelés: a teljes értékű következetes érvelés, pontosság és függetlenség igényének ápolása.

Fejlesztő: a matematikai logika fejlesztése, a matematikai gondolkodásmód kialakítása (az érvelés menetének egyértelmű boncolgatása), kognitív érdeklődés.

1) Bevezetés, az óra céljainak és célkitűzéseinek meghatározása - 2 perc.

2) Házi feladat ellenőrzése - 2 perc. (frontális munka, önkontroll).

3) Az egyenlőtlenségek megoldásának szakaszainak matematikai alátámasztása intervallum módszerrel - 4 perc (elkészített tanulói válaszok).

4) Egyenlőtlenségek tulajdonságainak ismétlődése – 2 perc.

5) Felkészülés új oktatási anyagok elsajátítására (tanulmányozására) ismétléssel, alapismeretek frissítésével – 5 perc. (frontmunka, kérdésekre adott válaszok, problémahelyzetek).

6) Intervallumok általánosított módszere egyenlőtlenségek megoldására, kezdeti megértés – 13 perc. (egyenlőtlenségek kollektív megoldása intervallum módszerrel: táblán és füzetekben).

7) Tájékoztatás a házi feladatról, kitöltési útmutató – 1 perc.

8) Új ismeretek megszilárdítása – 15 perc. (önálló munka – 1. lehetőség).

9) Az óra összegzése, elmélkedés – 1 perc.

1) Bevezetés, a tanórai célok és célkitűzések meghatározása. (tanár története)

1) Az intervallummódszer iskolai szélesebb körű alkalmazásának szükségességét a matematikatanítás egész folyamatának ideológiája diktálja. A lényeg az, hogy a funkcionális vonal (az egyik legfontosabb a matematika alapjainak tanulmányozásakor) erőteljes technológiai támogatást kap. Az intervallum-módszer a funkcionális függőség olyan fontos jellemzőin alapul, mint a függvény nullái, állandó előjelének intervallumai és monotonitása. Ekkor világosabbá válik az egyenletek és egyenlőtlenségek funkcionális eredete, valamint a megoldási módszerek. Világosabbá válnak egy függvény folytonossági kategóriái, gráfjának viselkedése végtelen diszkontinuitás pontok környezetében, gyöktételek, előjelállandóság, szélsőpontok és típusaik. És mindez szervesen kapcsolódik egyetlen funkcionális egésszé.

Másrészt felbecsülhetetlen a felhasznált kutatási objektumok geometrizáltsága is, i. vizuálisan és képletesen ábrázolják a funkcionális függőség összes használt matematikai eszközét.

Az intervallummódszer alapelvei:

• funkcionális (általánosított) megközelítés;
• a funkcionális tulajdonságok geometrizálására való hagyatkozás;
• kutatási vizualizáció.

Ez a módszer következő előnyeihez vezet az azonos típusú feladatoknál alkalmazott többi módszerhez képest: egyszerűség és a cél elérésének gyorsasága; láthatóság (és az ellenőrzés vagy a kettős ellenőrzés képessége); gazdaságosság a számítási erőforrások és idő tekintetében; a teljes helyzet lefedettségének szélessége, az általánosított gondolkodás és elemzés képességeinek kialakítása és fejlesztése, valamint az ehhez kapcsolódó logikus következtetések levonásának képessége.

2) Házi feladat ellenőrzése.(4. dia)

3) Egy történet az egyenlőtlenségek megoldásának intervallum módszeréről. (Diákok válaszai).

Egyenlőtlenségek megoldásának matematikai indoklása intervallummódszerrel.

1) Tekintsük az (x-2)(x-3)>0 egyenlőtlenségeket. (5. dia)

Megoldhatod a következőképpen: Két tényező szorzata (hányadosa) akkor és csak akkor pozitív, ha mindkét tényező azonos előjelű, pl. az egyenlőtlenség két rendszer kombinációjával ekvivalens: (6. sz. dia)

Az első rendszerből x >3, a másodikból x-et kapunk< 2.

A megoldás a két rendszer megoldásainak kombinálása.

Válasz:

Grafikus módszer (7. dia)

Egy másik módszer az intervallum módszer(8. dia).

Ötlete a következő.

Jelöljük a számegyenesen az (x-2)(x-3) polinom nulláit (gyökeit)

az egyenlőtlenség bal oldalán, azaz. 2. és 3. szám.

Ha x >3 (a nagyobb gyökértől jobbra), akkor (x-2)(x-3)>0, mivel minden tényező pozitív.

Ha a tengely mentén negatív irányba mozog, akkor az x=3 ponton való áthaladáskor az (x-3) tényező előjelet vált. Az (x-2)(x-3) szorzatban egy negatív tényező jelenik meg, ami (x-2)(x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Most már könnyű megírni az egyenlőtlenség megoldását:

Következtetés: a szorzat csak az x=2 és x=3 pontokon áthaladva változtathat előjelet

és ezért megőrzi a jelet az egyes eredő intervallumokon.

Ebből az egyszerű példából könnyen megérthető az intervallummódszer gondolata, de nem mutatja meg jelentős előnyeit.

Tekintsük az intervallummódszer racionalitását és erejét a következő példában (9., 10.,11., 12. dia)!

2) Oldja meg az (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) egyenlőtlenséget. (x-10)>0.

Ennek az egyenlőtlenségnek a rendszerhalmaz segítségével történő megoldásához egy 512 rendszerből álló halmazt kell figyelembe venni, mindegyik rendszerben 10 egyenlőtlenséggel.

Használjuk az intervallum módszert. Jelöljük a polinom nulláit a számegyenesen. Az x>10 intervallumon a polinom pozitív lesz, mivel minden tényező pozitív. Minden következő gyökön áthaladva a polinom előjelet vált, mivel egy további negatív tényező jelenik meg a szorzatban. Most már könnyű felírni az egyenlőtlenség megoldását váltakozó előjelekkel.

Az intervallum módszer előnyei.

• a cél elérésének egyszerűsége és gyorsasága;
• láthatóság (és az ellenőrzés vagy a kettős ellenőrzés képessége);
• a számítási munka és idő jelentős csökkenése;
• a teljes helyzet lefedettsége;
• az általánosított gondolkodás és elemzés készségeinek kialakítása és fejlesztése, valamint az ehhez kapcsolódó logikus következtetések levonására való képesség.

Megjegyzés. Nagyon kényelmes megoldani az egyenlőtlenségeket, amelyek bal oldala faktorizált, mivel nem nehéz megtalálni a nullákat (gyököket).

Feladat: Oldja meg az egyenlőtlenséget intervallum módszerrel! (x+3) 3 (x-4) 2 (x-5)>0(13. dia)

4) Az egyenlőtlenségek tulajdonságainak ismétlődése.

a) Kérdés: Milyen egyenlőtlenségeket nevezünk ekvivalensnek?

(Két egyenlőtlenséget ekvivalensnek mondunk, ha az első egyenlőtlenség bármely megoldása a második megoldása, és fordítva, a második egyenlőtlenség bármely megoldása az első megoldása).

Vagy: két egyenlőtlenséget ekvivalensnek nevezünk, ha megoldásaik halmazai egybeesnek.

14. dia. Egyenlőtlenségek tulajdonságainak ismétlődése.

15. dia. Válaszoljon a kérdésre, és magyarázza el.

Egyenértékűek az egyenlőtlenségek?

1) 4x-5<0 и 4х<5

2) -2x+5>0 és 2x-5<0

3) -3x 2 +5x-7>0 és 3x 2 -5x+7<0

4) (x+1)>0 és (x2 +5x+10) (x+1)>0

5) Szóbeli frontális munka az új oktatási anyagok asszimilálására (tanulmányozására) az alapismeretek ismétlésével és frissítésével történő felkészítés.

16. dia. Egy pontban folytonos függvény definíciója.

17. dia. Folyamatos függvények tulajdonsága.

18. dia. Keresse meg a folytonossági intervallumokat.

19. dia Keresse meg a hibát.

20. dia. Oldja meg az egyenlőtlenséget szóban,
diagram segítségével.

21., 22. dia. Az egyenlőtlenség helyettesítése egyenértékű feltétellel.

Oldja meg az egyenlőtlenséget

Ez az egyenlőtlenség ekvivalens az f(x) feltétellel < 0, számolva

Ezért meg kell találnunk x minden olyan értékét, amelyre az f(x) feltétel teljesül < 0.

6) Intervallumok általánosított módszere egyenlőtlenségek megoldására, kezdeti megértés – 10 perc. (egyenlőtlenségek kollektív megoldása intervallum módszerrel: táblán és füzetekben).

23. dia. Algoritmus. Általánosított módszer az egyenlőtlenségek megoldására.

Egyenlőtlenségek megoldása f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 intervallum módszerrel. (Rendszer)

24. és 25. dia. Egyenlőtlenségek megoldása algoritmus segítségével. (Megjegyzések az algoritmus minden pontjához).

26. dia. Ennek az egyenlőtlenségnek a megoldásának grafikus ábrázolása.

27. dia. Oldja meg az egyenlőtlenségeket a táblán és a füzetekben! .

28. dia. Ennek az egyenlőtlenségnek a megoldásának grafikus ábrázolása.

29. dia. Oldja meg az egyenlőtlenségeket a táblán és a füzetekben!

30. dia. Ennek az egyenlőtlenségnek a megoldásának grafikus ábrázolása.

31., 32. dia. Oldja meg az egyenlőtlenséget szóban, kép segítségével!

7) Információk a házi feladatról.(Megoldása intervallum módszerrel 2. lehetőség)

8) Új ismeretek megszilárdítása (önálló munka, 1. lehetőség).

9) Óra összegzése, önkontroll kész megoldásokkal (33., 34., 35. dia), az általánosított intervallum módszer algoritmusának megismétlése és alkalmazása.

10) A tanulók tanulásának és a téma iránti érdeklődésének elemzése. Ez a módszer univerzális bármilyen egyenlőtlenség megoldására, beleértve a racionális, modulus, irracionális, exponenciális, logaritmikus egyenlőtlenségeket, mivel az intervallumok megoldása az egyenlőtlenségek megoldását az egyenletek megoldására redukálja nem okoz nehézségeket. De példákat kellett hoznom olyan egyenlőtlenségekre, ahol nem indokolt ennek a módszernek az alkalmazása, ahol ésszerűbb más módszereket alkalmazni az egyenlőtlenségek megoldására.

„A folytonosság alkalmazása az egyenlőtlenségek megoldásában” című előadás. (35 dia)

Meghatározás. Legyen egy f(x) függvény definiálva valamilyen intervallumon, és legyen x 0 egy pont ebben az intervallumban. Ha , akkor f(x) folytonosnak mondható az x 0 pontban.
A definícióból az következik, hogy folytonosságról csak azokra a pontokra vonatkoztatva beszélhetünk, ahol f(x) definiálva van (egy függvény határértékének meghatározásakor ilyen feltételt nem állítottunk fel). Folyamatos funkciókhoz , azaz az f és a lim műveletek kommutálhatóak. Ennek megfelelően egy függvény határértékének egy pontban két definíciója adható a folytonosság két definíciójához - „a sorozatok nyelvén” és „az egyenlőtlenségek nyelvén” (ε-δ nyelvén). Javasoljuk, hogy ezt saját maga végezze el.
Gyakorlati használatra néha kényelmesebb a folytonosság meghatározása a növekmény nyelvén.
A Δx=x-x 0 értéket az argumentum növekményének nevezzük, Δy=f(x)-f(x 0) pedig a függvény növekményét, amikor x 0 pontból x pontba lépünk.
Meghatározás. Legyen f(x) az x 0 pontban. Egy f(x) függvényt folytonosnak nevezünk egy x 0 pontban, ha az argumentum végtelen kis növekménye ebben a pontban megfelel a függvény végtelen kicsi növekményének, azaz Δy→0 Δx→0 esetén.

1. példa Bizonyítsuk be, hogy az y=sinx függvény folytonos x bármely értékére.
Megoldás. Legyen x 0 tetszőleges pont. Ha Δx növekményt adunk neki, megkapjuk az x=x 0 +Δx pontot. Akkor . Kapunk .
Meghatározás. Az y=f(x) függvényt folytonosnak nevezzük a jobb (bal) x 0 pontban, ha
.
Egy belső pontban folytonos függvény jobbra és balra is folyamatos lesz. Ennek a fordítottja is igaz: ha egy függvény folytonos a bal és a jobb oldalon lévő pontban, akkor az adott pontban folytonos lesz. Egy függvény azonban csak az egyik oldalon lehet folytonos. Például azért , , f(1)=1, ezért ez a függvény csak a bal oldalon folytonos (a függvény grafikonját lásd fent az 5.7.2. bekezdésben).
Meghatározás. Egy függvényt folytonosnak nevezünk valamely intervallumon, ha az ennek az intervallumnak minden pontjában folytonos.
Különösen, ha az intervallum egy szegmens, akkor a végei egyoldalú folytonosságra utalnak.

A folytonos függvények tulajdonságai

1. Minden elemi függvény folytonos a definíciós tartományában.
2. Ha egy bizonyos intervallumon adott f(x) és φ(x) ennek az intervallumnak az x 0 pontjában folytonosak, akkor a függvények ebben a pontban is folytonosak lesznek.
3. Ha y=f(x) folytonos az x 0 pontban X-ből, és z=φ(y) folytonos a megfelelő y 0 =f(x 0) pontban Y-ból, akkor a z=φ komplex függvény (f(x )) folytonos lesz az x 0 pontban.

A funkciótörések és osztályozásuk

Az f(x) függvény folytonosságának jele az x 0 pontban az egyenlőség, amely három feltétel meglétét jelenti:
1) f(x) az x 0 pontban van definiálva;
2) ;
3) .
Ha ezen követelmények közül legalább egy megsértődik, akkor x 0-t a függvény töréspontjának nevezzük. Más szóval, a töréspont az a pont, ahol ez a függvény nem folyamatos. A töréspontok definíciójából következik, hogy egy függvény töréspontjai a következők:
a) a függvény definíciós tartományába tartozó pontok, amelyeknél f(x) elveszti a folytonossági tulajdonságát,
b) f(x) definíciós tartományába nem tartozó pontok, amelyek a függvény definíciós tartományának két intervallumának szomszédos pontjai.
Például egy függvénynél az x=0 pont töréspont, mivel a függvény ezen a ponton nincs definiálva, és a függvény diszkontinuitása van az f(x) definíciós tartományának két (-∞,1) és (1,∞) intervallumával szomszédos x=1 pontban, és nem létezik.

A következő besorolást alkalmazzuk a töréspontokhoz.
1) Ha az x 0 pontban végesek vannak És , de f(x 0 +0)≠f(x 0 -0), akkor x 0-t hívunk az első típusú megszakítási pont , és hívják funkcióugrás .

2. példa Fontolja meg a funkciót
A függvény csak az x=2 pontban törhető (más pontokban folytonos, mint bármely polinom).
meg fogjuk találni , . Mivel az egyoldali határértékek végesek, de nem egyenlőek egymással, ezért az x=2 pontban a függvénynek van egy első típusú diszkontinuitása. vegye észre, az , ezért a függvény ezen a ponton a jobb oldalon folytonos (2. ábra).
2) Második típusú megszakítási pontok pontoknak nevezzük, ahol az egyoldali határértékek legalább egyike egyenlő ∞-vel, vagy nem létezik.

3. példa Az y=2 1/x függvény folytonos x minden értékére, kivéve x=0. Keressünk egyoldalú korlátokat: , , ezért x=0 egy második típusú szakadási pont (3. ábra).
3) Az x=x 0 pontot hívjuk kivehető töréspont , ha f(x 0 +0)=f(x 0 -0)≠f(x 0).
A rést abban az értelemben „kiküszöböljük”, hogy ezen a ponton elég megváltoztatni (újradefiniálni vagy újradefiniálni) a függvény értékét a beállítással, és a függvény az x 0 pontban folytonossá válik.
4. példa Ismeretes, hogy , és ez a határ nem függ attól, hogy x hogyan hajlik nullára. De az x=0 pontban lévő függvény nincs definiálva. Ha a függvényt újradefiniáljuk f(0)=1 beállítással, akkor ezen a ponton folytonosnak bizonyul (más pontokon a sinx és x folytonos függvények hányadosaként folytonos).
5. példa. Vizsgálja meg egy függvény folytonosságát! .
Megoldás. Az y=x 3 és y=2x függvények mindenhol definiáltak és folytonosak, a jelzett intervallumokban is. Vizsgáljuk meg az x=0 intervallumok találkozási pontját:
, , . Azt kapjuk, hogy , ami azt jelenti, hogy az x=0 pontban a függvény folytonos.
Meghatározás. Azt a függvényt, amely egy intervallumon folytonos, kivéve az első típusú vagy eltávolítható szakadási pontok véges számát, ezen az intervallumon darabonként folytonosnak nevezzük.

Példák nem folytonos funkciókra

1. példa A függvény definiált és folytonos be (-∞,+∞), kivéve az x=2 pontot. Határozzuk meg a szünet típusát. Mert a És , akkor az x=2 pontban egy második típusú szakadás van (6. ábra).
2. példa A függvény definiált és folytonos minden x-re, kivéve x=0, ahol a nevező nulla. Keressünk egyoldalú határértékeket az x=0 pontban:
Az egyoldali határértékek végesek és különbözőek, ezért x=0 az első típusú szakadási pont (7. ábra).
3. példa Határozza meg, hogy mely pontokon és milyen szakadásai vannak a függvénynek!
Ez a függvény a [-2,2]-en van definiálva. Mivel x 2 és 1/x folytonos a [-2,0], illetve a intervallumokban, ezért a folytonossági zavar csak az intervallumok találkozásánál, azaz az x=0 pontban fordulhat elő. Mivel , akkor x=0 egy második típusú szakadási pont.

4. példa Kiküszöbölhetők-e a funkcióhézagok:
a) az x=2 pontban;
b) pontban x=2;
V) x=1 pontban?
Megoldás. Az a) példáról azonnal elmondhatjuk, hogy az x=2 pontban az f(x) szakadást nem lehet kiküszöbölni, mivel ezen a ponton végtelen egyoldalú határérték van (lásd 1. példa).
b) A g(x) függvénynek véges egyoldalú határértékei vannak az x=2 pontban

(,),

de nem esnek egybe, így a szakadék sem szüntethető meg.
c) A φ(x) függvénynek az x=1 szakadási pontban egyenlő egyoldalú véges határai vannak: . Ezért a rés kiküszöbölhető az x=1-es függvény újradefiniálásával, ha f(1)=2 helyett f(1)=1-et teszünk.

5. példa. Mutassuk meg, hogy a Dirichlet függvény

nem folytonos a numerikus tengely minden pontjában.
Megoldás. Legyen x 0 a (-∞,+∞) bármely pontja. Bármelyik szomszédságában vannak racionális és irracionális pontok. Ez azt jelenti, hogy x 0 bármely környezetében a függvénynek 0 és 1 értéke lesz. Ebben az esetben a függvény határértéke az x 0 pontban nem létezhet sem a bal, sem a jobb oldalon, ami azt jelenti, hogy a Dirichlet-függvénynek a valós tengely minden pontjában másodlagos folytonossági zavarai vannak.

6. példa. Funkciótöréspontok keresése

és meghatározzák a típusukat.
Megoldás. A törésre gyanús pontok az x 1 =2, x 2 =5, x 3 =3 pontok.
Az x 1 =2 pontban f(x)-nek van egy második típusú szakadása, mivel
.
Az x 2 =5 pont egy folytonossági pont, mivel a függvény értékét ebben a pontban és annak közelében a második egyenes határozza meg, és nem az első: .
Vizsgáljuk meg az x 3 =3 pontot: , , amiből az következik, hogy x=3 egy első típusú szakadási pont.

Önálló döntésre.
Vizsgálja meg a folytonossági függvényeket, és határozza meg a folytonossági pontok típusát:
1) ; Válasz: x=-1 – eltávolítható folytonossági pont;
2) ; Válasz: Második típusú szakadás az x=8 pontban;
3) ; Válasz: Az első típusú megszakadás x=1-nél;
4)
Válasz: Az x 1 =-5 pontban eltávolítható rés van, az x 2 =1 pontban egy második típusú rés, az x 3 =0 pontban pedig az első típusú rés.
5) Hogyan kell az A számot kiválasztani, hogy a függvény

folytonos lenne x=0-nál?
Válasz: A=2.
6) Kiválasztható-e az A szám úgy, hogy a függvény

folytonos lenne x=2-nél?
Válasz: nem.

A funkció folytonossága. Kitörési pontok.

A bika sétál, ringatóz, sóhajt menet közben:
- Ó, fogy a deszka, most lezuhanok!

Ebben a leckében megvizsgáljuk a függvény folytonosságának fogalmát, a szakadási pontok osztályozását és egy gyakori gyakorlati problémát. függvények folytonossági vizsgálata. Sokan már a téma nevéből is kitalálják, hogy miről lesz szó, és azt gondolják, hogy az anyag meglehetősen egyszerű. Ez igaz. De az egyszerű feladatokat leggyakrabban elhanyagolásért és a megoldásuk felületes megközelítéséért büntetik. Ezért azt javaslom, hogy alaposan tanulmányozza át a cikket, és ismerje meg az összes finomságot és technikát.

Mit kell tudni és tudni kell? Nem nagyon. Ahhoz, hogy jól megtanuld a leckét, meg kell értened, mi az függvény határértéke. Az alacsony felkészültségű olvasók számára elegendő a cikk megértése Funkciókorlátok. Példák megoldásokraés nézd meg a határérték geometriai jelentését a kézikönyvben Elemi függvények grafikonjai és tulajdonságai. Szintén tanácsos megismerkedni gráfok geometriai transzformációi, mivel a gyakorlat a legtöbb esetben egy rajz elkészítésével jár. A kilátások mindenki számára bizakodóak, és a következő egy-két órában egy teli vízforraló is megbirkózik magával a feladattal!

A funkció folytonossága. Töréspontok és osztályozásuk

A funkció folytonosságának fogalma

Tekintsünk egy olyan függvényt, amely a teljes számegyenesen folytonos:

Vagy tömörebben fogalmazva a függvényünk folytonos on (valós számok halmaza).

Mi a folytonosság „filiszteus” kritériuma? Nyilvánvaló, hogy egy folytonos függvény grafikonja megrajzolható anélkül, hogy felemelné a ceruzát a papírról.

Ebben az esetben két egyszerű fogalmat kell egyértelműen megkülönböztetni: egy függvény tartományaÉs a funkció folytonossága. Általában ez nem ugyanaz. Például:

Ez a függvény a teljes számegyenesen van definiálva, azaz for mindenki Az „x” jelentésének megvan a maga „y” jelentése. Különösen, ha , akkor . Figyeljük meg, hogy a másik pont írásjeles, mert a függvény definíciója szerint az argumentum értékének meg kell felelnie Az egyetlen dolog függvény értéke. És így, tartomány funkciónk: .

azonban ez a funkció nem folyamatos! Teljesen nyilvánvaló, hogy pont szenved rés. A kifejezés is eléggé érthető, valóban, itt a ceruzát úgyis le kell majd tépni a papírról. Kicsit később megnézzük a töréspontok osztályozását.

Egy függvény folytonossága egy pontban és egy intervallumon

Egy adott matematikai feladatban beszélhetünk egy függvény folytonosságáról egy ponton, egy függvény folytonosságáról egy intervallumon, egy félintervallumról vagy egy függvény folytonosságáról egy szakaszon. vagyis nincs "csupán folytonosság"– a függvény VALAHOL folyamatos lehet. És minden más alapvető „építőköve”. a funkció folytonossága azon a ponton .

A matematikai analízis elmélete „delta” és „epszilon” körzetek segítségével definiálja egy függvény folytonosságát egy pontban, de a gyakorlatban ettől eltérő definíció van használatban, amelyre kiemelt figyelmet fordítunk.

Először is emlékezzünk egyoldalú határok aki az első leckében berobbant az életünkbe a függvénygrafikonokról. Vegyünk egy mindennapi helyzetet:

Ha a ponthoz közelítjük a tengelyt bal(piros nyíl), akkor a „játékok” megfelelő értékei a tengely mentén a pontig mennek (bíbor nyíl). Matematikailag ezt a tényt a segítségével rögzítjük bal oldali határ:

Ügyeljen a bejegyzésre (a bal oldalon „x hajlamos a ka-ra”). Az „adalék” „mínusz nulla” jelképezi , ez lényegében azt jelenti, hogy bal oldalról közelítünk a számhoz.

Hasonlóképpen, ha a „ka” ponthoz közelítünk jobb oldalon(kék nyíl), akkor a „játékok” azonos értékűek lesznek, de a zöld nyíl mentén, és jobb oldali határ a következőképpen lesz formázva:

Az "adalék" szimbolizálja , és a bejegyzés így hangzik: „x a jobb oldalon a ka-ra irányul.”

Ha az egyoldali határértékek végesek és egyenlőek(mint a mi esetünkben): , akkor azt mondjuk, hogy van egy ÁLTALÁNOS korlát. Egyszerű, az általános határ a mi „szokásunk” függvény határértéke, egyenlő egy véges számmal.

Vegye figyelembe, hogy ha a függvény nincs definiálva (dugja ki a fekete pontot a grafikon ágán), akkor a fenti számítások érvényben maradnak. Amint azt többször is megjegyezték, különösen a cikkben végtelenül kicsi függvényeken, kifejezések azt jelentik, hogy "x" végtelenül közel közeledik a lényeghez, miközben NEM SZÁMÍT, hogy maga a függvény definiált-e egy adott pontban vagy sem. Egy jó példát találunk a következő bekezdésben, amikor a függvényt elemezzük.

Meghatározás: egy függvény folytonos egy pontban, ha a függvény határértéke egy adott pontban egyenlő a függvény értékével abban a pontban: .

A meghatározást a következő kifejezések részletezik:

1) A függvényt a ponton kell definiálni, vagyis az értéknek léteznie kell.

2) A függvénynek meg kell lennie egy általános korlátnak. Amint fentebb megjegyeztük, ez egyoldalú korlátok létezését és egyenlőségét jelenti: .

3) A függvény határértékének egy adott pontban meg kell egyeznie a függvény értékével ebben a pontban: .

Ha megsértették legalább egy a három feltétel közül, akkor a függvény elveszti a folytonosság tulajdonságát a pontban.

Egy függvény folytonossága egy intervallumon keresztül zseniálisan és nagyon egyszerűen van megfogalmazva: egy függvény folytonos az intervallumon, ha az adott intervallum minden pontjában folytonos.

Különösen sok függvény folytonos egy végtelen intervallumon, azaz a valós számok halmazán. Ez egy lineáris függvény, polinomok, exponenciális, szinusz, koszinusz stb. És általában bármilyen elemi funkció folyamatos rajta definíciós tartomány például egy logaritmikus függvény folytonos az intervallumon. Remélhetőleg mostanra már elég jó elképzelése van arról, hogyan néznek ki az alapvető függvények grafikonjai. Folyamatosságukról egy Fichtenholtz nevű kedves embertől kaphatunk részletesebb információkat.

Egy függvény folytonossága egy szegmensen és félintervallumokkal szintén nem nehéz, de célszerűbb erről beszélni az órán egy függvény minimális és maximális értékének megtalálásáról egy szakaszon, de egyelőre ne törődjünk vele.

A töréspontok osztályozása

A funkciók lenyűgöző élete mindenféle különleges pontban gazdag, a töréspontok pedig életrajzuknak csak egy lapja.

jegyzet : minden esetre kitérek egy elemi pontra: a töréspont mindig az egyetlen pont– nincs „több töréspont egymás után”, vagyis nincs olyan, hogy „szünetköz”.

Ezek a pontok viszont két nagy csoportra oszthatók: az első típusú szakadásokÉs a második típusú szakadások. Minden réstípusnak megvannak a saját jellemzői, amelyeket most megvizsgálunk:

Az első típusú megszakítási pont

Ha a folytonossági feltételt egy ponton megsértik és egyoldalú korlátok véges , akkor úgy hívják az első típusú megszakítási pont.

Kezdjük a legoptimistább esettel. A lecke eredeti elképzelése szerint az elméletet "általánosan" szerettem volna elmondani, de az anyag valóságának bemutatása érdekében a konkrét karakterek opciója mellett döntöttem.

Szomorú, mint az ifjú házasok fotója az örök láng hátterében, de a következő felvétel általánosan elfogadott. Ábrázoljuk a függvény grafikonját a rajzon:


Ez a függvény a pont kivételével a teljes számegyenesen folyamatos. És valójában a nevező nem lehet egyenlő nullával. A korlát jelentésének megfelelően azonban megtehetjük végtelenül közel balról és jobbról is megközelíti a „nullát”, vagyis léteznek egyoldalú határok, és nyilvánvalóan egybeesnek:
(A folytonosság 2. feltétele teljesül).

De a függvény a ponton nincs definiálva, ezért a folytonosság 1. feltétele sérül, és a függvény ezen a ponton megszakadást szenved.

Egy ilyen típusú szünet (a meglévővel általános határérték) hívják javítható hézag. Miért eltávolítható? Mert a függvény képes újradefiniál a törésponton:

Furcsán néz ki? Talán. De egy ilyen függvényjelölés semminek sem mond ellent! Most a szakadék bezárult, és mindenki boldog:


Végezzünk el egy formális ellenőrzést:

2) – van egy általános korlát;
3)

Így mindhárom feltétel teljesül, és a függvény egy pontban folytonos a függvény folytonosságának meghatározása szerint egy pontban.

A matan gyűlölők azonban például rosszul definiálhatják a funkciót :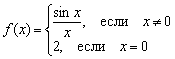


Érdekes, hogy itt az első két folytonossági feltétel teljesül:
1) – a függvény egy adott pontban van definiálva;
2) – van egy általános határ.

De a harmadik határt nem léptük át: , vagyis a függvény határát a pontban nem egyenlő egy adott függvény értéke egy adott pontban.

Így a függvény egy ponton megszakadást szenved.

A második, szomorúbb eset az ún az első típusú szakadás egy ugrással. A szomorúságot pedig egyoldalú korlátok váltják ki, hogy véges és különböző. Egy példa látható a lecke második rajzán. Az ilyen rés általában akkor fordul elő darabonként meghatározott függvények, amelyekről a cikkben már szó esett gráftranszformációkról.

Tekintsük a darabonkénti függvényt és befejezzük a rajzát. Hogyan készítsünk grafikont? Nagyon egyszerű. Fél intervallumon egy parabola töredéket (zöld), egy intervallumon - egy egyenes szakaszt (piros) és egy fél intervallumon - egy egyenest (kék) rajzolunk.

Ráadásul az egyenlőtlenség miatt a másodfokú függvény értéke (zöld pont), az egyenlőtlenség miatt pedig a lineáris függvény (kék pont) értékét határozza meg:

A legnehezebb esetben a grafikon minden egyes darabjának pontról pontra történő felépítéséhez kell folyamodnia (lásd az elsőt lecke a függvénygrafikonokról).

Most már csak a lényeg fog minket érdekelni. Vizsgáljuk meg a folytonosság szempontjából:

2) Számítsunk egyoldalú határértékeket.

A bal oldalon van egy piros vonalszakasz, így a bal oldali határ a következő:

A jobb oldalon a kék egyenes vonal és a jobb oldali határ:

Ennek eredményeként megkaptuk véges számok, és ők nem egyenlő. Mivel az egyoldalú korlátok véges és különböző: , akkor funkciónk tolerálja az első fajta folytonossági zavar ugrással.

Logikus, hogy a rést nem lehet megszüntetni - a függvényt valóban nem lehet tovább definiálni és „összeragasztani”, mint az előző példában.

Második típusú megszakítási pontok

Általában az összes többi szakadási esetet ügyesen ebbe a kategóriába sorolják. Nem sorolok fel mindent, mert a gyakorlatban a problémák 99%-ában találkozni fog végtelen szakadék– ha balkezes vagy jobbkezes, és gyakrabban mindkét határ végtelen.

És természetesen a legszembetűnőbb kép a nullapontban lévő hiperbola. Itt mindkét egyoldalú határ végtelen: , ezért a függvény a pontban másodlagos folytonossági hiányt szenved.

Cikkeimet igyekszem minél változatosabb tartalommal megtölteni, ezért nézzünk egy olyan függvény grafikonját, amivel még nem találkoztunk:

szabványos séma szerint:

1) A függvény ezen a ponton nincs meghatározva, mert a nevező nullára megy.

Természetesen azonnal levonhatjuk azt a következtetést, hogy a függvény pontban megszakadást szenved, de jó lenne osztályozni a folytonossági zavar jellegét, amit a feltétel gyakran megkövetel. Ezért:

Hadd emlékeztesselek arra, hogy a felvétel alatt azt értjük végtelenül kicsi negatív szám, és a bejegyzés alatt - végtelenül kicsi pozitív szám.

Az egyoldalú határértékek végtelenek, ami azt jelenti, hogy a függvény 2. típusú folytonossági hiányt szenved a pontban. Az y tengely az függőleges aszimptota a grafikonhoz.

Nem ritka, hogy mindkét egyoldalú határ létezik, de csak az egyik végtelen, pl.

Ez a függvény grafikonja.

Megvizsgáljuk a folytonosságot:

1) A függvény ezen a ponton nincs meghatározva.

2) Számítsunk egyoldalú határértékeket: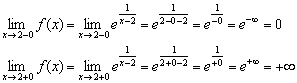

Az ilyen egyoldalú határértékek kiszámításának módszeréről az előadás utolsó két példájában lesz szó, bár sok olvasó már mindent látott és kitalált.

A bal oldali határ véges és egyenlő nullával (magához a ponthoz nem megyünk), a jobb oldali határ viszont végtelen, és a gráf narancssárga ága végtelenül közelít a függőleges aszimptota, amelyet az egyenlet (fekete pontozott vonal) ad meg.

Tehát a funkció szenved második fajta folytonossági hiány pontban.

Ami az 1. típusú megszakítást illeti, a függvény magában a megszakítási pontban definiálható. Például egy darabonkénti függvényhez Nyugodtan tegyen egy fekete félkövér pontot a koordináták origójába. A jobb oldalon egy hiperbola ága látható, a jobb oldali határ pedig végtelen. Azt hiszem, szinte mindenkinek van fogalma arról, hogy néz ki ez a grafikon.

Amit mindenki nagyon várt:

Hogyan vizsgáljunk meg egy függvényt a folytonosság szempontjából?

Egy pontban a folytonosság függvényének vizsgálata egy már kialakított rutinséma szerint történik, amely a folytonosság három feltételének ellenőrzéséből áll:

1. példa

Funkció felfedezése

Megoldás:

1) A hatókörön belül az egyetlen pont az, ahol a függvény nincs definiálva.

2) Számítsunk egyoldalú határértékeket: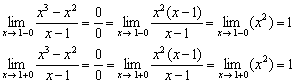

Az egyoldalú határértékek végesek és egyenlőek.

Így azon a ponton a függvény eltávolítható folytonossági hiányt szenved.

Hogyan néz ki ennek a függvénynek a grafikonja?

Szeretnék egyszerűsíteni , és úgy tűnik, egy közönséges parabolát kapunk. DE pontban az eredeti függvény nincs definiálva, ezért a következő záradék szükséges:

Készítsük el a rajzot:

Válasz: a függvény folytonos a teljes számegyenesen, kivéve azt a pontot, ahol eltávolítható folytonossági hiányt szenved.

A függvény tovább definiálható jó vagy nem túl jó módon, de a feltételtől függően ez nem szükséges.

Azt mondod, ez egy távoli példa? Egyáltalán nem. Ez a gyakorlatban több tucatszor megtörtént. Az oldal szinte minden feladata valódi független munkából és tesztekből származik.

Megszabadulunk kedvenc moduljainktól:

2. példa

Funkció felfedezése a folytonosság érdekében. Határozza meg a függvényszakadások természetét, ha léteznek. Hajtsa végre a rajzot.

Megoldás: Valamiért a hallgatók félnek és nem szeretik a modulos függvényeket, pedig nincs bennük semmi bonyolult. A leckében már érintettünk egy kicsit ilyesmit. Gráfok geometriai transzformációi. Mivel a modul nem negatív, a következőképpen bővül: , ahol az „alfa” valamilyen kifejezés. Ebben az esetben a függvényünket darabonként kell felírni:

De mindkét darab törtrészét csökkenteni kell -vel. A csökkentés az előző példához hasonlóan nem megy következmények nélkül. Az eredeti függvény nincs definiálva a ponton, mivel a nevező nullára megy. Ezért a rendszernek ezenkívül meg kell adnia a feltételt, és szigorúvá kell tennie az első egyenlőtlenséget:

Most egy NAGYON HASZNOS döntési technikáról: a feladat tervezeten történő véglegesítése előtt előnyös rajzot készíteni (függetlenül attól, hogy a feltételek megkívánják vagy sem). Ez egyrészt segít azonnal látni a folytonossági pontokat és a megszakadási pontokat, másrészt 100%-ban megvédi Önt a hibáktól az egyoldalú határok megtalálásakor.

Csináljuk a rajzot. Számításaink szerint a ponttól balra egy parabola töredéket kell rajzolni (kék szín), jobbra pedig egy parabola darabot (piros szín), míg a függvény nincs meghatározva a maga a pont:

Ha kétségei vannak, vegyen néhány x értéket, és csatlakoztassa őket a függvényhez (ne feledje, hogy a modul megsemmisíti a lehetséges mínuszjelet), és ellenőrizze a grafikont.

Vizsgáljuk meg analitikusan a folytonosság függvényét:

1) A függvény a ponton nincs definiálva, így azonnal kijelenthetjük, hogy nem folytonos benne.

2) Határozzuk meg a folytonossági hiány jellegét, egyoldalú határértékeket számolunk:

Az egyoldalú határértékek végesek és különbözőek, ami azt jelenti, hogy a függvény az 1. típusú folytonossági hiányt szenved a pontban történő ugrással. Megjegyezzük még egyszer, hogy a határértékek megtalálásakor nem számít, hogy a töréspontban lévő függvény definiálva van-e vagy sem.

Most már csak át kell vinni a rajzot a vázlatból (mintha kutatás segítségével készült ;-)) és teljesíteni a feladatot:

Válasz: a függvény folytonos a teljes számegyenesen, kivéve azt a pontot, ahol egy ugrással az első típusú folytonossági hiányt szenved.

Néha további jelzést igényelnek a folytonossági ugrásról. Kiszámítása egyszerűen történik - a jobb oldali határból le kell vonni a bal határt: , vagyis a töréspontnál a függvényünk 2 egységet ugrott lejjebb (ahogy a mínusz jel is mondja).

3. példa

Funkció felfedezése a folytonosság érdekében. Határozza meg a függvényszakadások természetét, ha léteznek. Készítsen rajzot.

Ez egy példa, amelyet önállóan kell megoldania, mintamegoldás a lecke végén.

Térjünk át a feladat legnépszerűbb és legelterjedtebb változatára, amikor a funkció három részből áll:

4. példa

Vizsgáljunk meg egy függvényt a folytonosságra, és ábrázoljuk a függvény grafikonját .

Megoldás: nyilvánvaló, hogy a függvény mindhárom része folytonos a megfelelő intervallumokon, így csak két „csomópontot” kell ellenőrizni a darabok között. Először készítsünk vázlatrajzot a cikk első részében kellő részletességgel kommentáltam az építési technikát. Az egyetlen dolog, hogy gondosan követni kell az egyes pontjainkat: az egyenlőtlenség miatt az érték az egyeneshez (zöld pont), az egyenlőtlenség miatt pedig a parabolához (piros pont) tartozik:


Nos, elvileg minden világos =) Már csak a döntés formalizálása van hátra. A két „csatlakozási” pont mindegyikénél általában 3 folytonossági feltételt ellenőrizünk:

ÉN) Megvizsgáljuk a lényeget a folytonosság szempontjából

1)

Az egyoldalú határértékek végesek és különbözőek, ami azt jelenti, hogy a függvény az 1. típusú folytonossági hiányt szenved a pontban történő ugrással.

Számítsuk ki a folytonossági ugrást a jobb és bal határ közötti különbségként:
, vagyis a grafikon egy egységgel feljebb rándult.

II) Megvizsgáljuk a lényeget a folytonosság szempontjából

1) – a függvény egy adott pontban van definiálva.

2) Keresse meg az egyoldalú határokat:

– az egyoldalú határértékek végesek és egyenlőek, ami azt jelenti, hogy van egy általános határ.

3) – egy függvény határértéke egy pontban egyenlő ennek a függvénynek az értékével egy adott pontban.

Az utolsó szakaszban átvisszük a rajzot a végső verzióba, majd feltesszük a végső akkordot:

Válasz: a függvény a teljes számegyenesen folytonos, kivéve azt a pontot, ahol egy ugrással az első típusú folytonossági hiányt szenved.

5. példa

Vizsgáljunk meg egy függvényt a folytonosságra, és készítsük el a gráfját .

Ez egy példa az önálló megoldásra, egy rövid megoldás és egy hozzávetőleges minta a feladatból a lecke végén.

Azt a benyomást keltheti, hogy a függvénynek egy ponton folytonosnak kell lennie, a másikon pedig megszakításnak kell lennie. A gyakorlatban ez nem mindig van így. Ne hagyja figyelmen kívül a fennmaradó példákat - számos érdekes és fontos funkció lesz:

6. példa

Adott egy függvény . Vizsgáljuk meg a pontokban a folytonosság függvényét. Készítsen grafikont.

Megoldás: és ismét azonnal hajtsa végre a rajzot a piszkozaton:

Ennek a grafikonnak az a sajátossága, hogy a darabonkénti függvényt az abszcissza tengely egyenlete adja meg. Itt ez a terület zölddel van megrajzolva, de egy jegyzetfüzetben általában egy egyszerű ceruzával félkövérrel kiemelve. És persze ne feledkezzünk meg a kosainkról sem: az érték az érintő ághoz (piros pont), az érték pedig az egyeneshez tartozik.

A rajzból minden világos - a függvény a teljes számegyenesen folyamatos, csak formalizálni kell a megoldást, amely szó szerint 3-4 hasonló példa után teljes automatizálásra kerül:

ÉN) Megvizsgáljuk a lényeget a folytonosság szempontjából

1) – a függvény egy adott pontban van definiálva.

2) Számítsunk egyoldalú határértékeket:

, ami azt jelenti, hogy van egy általános korlát.

Minden esetre hadd emlékeztessek egy triviális tényre: egy állandó határértéke megegyezik magával az állandóval. Ebben az esetben a nulla határértéke megegyezik magával a nullával (bal oldali határ).

3) – egy függvény határértéke egy pontban egyenlő ennek a függvénynek az értékével egy adott pontban.

Így egy függvény egy pontban folytonos a függvény folytonosságának meghatározása szerint egy pontban.

II) Megvizsgáljuk a lényeget a folytonosság szempontjából

1) – a függvény egy adott pontban van definiálva.

2) Keresse meg az egyoldalú határokat:

És itt – az egy határa magával az egységgel egyenlő.

– van egy általános határ.

3) – egy függvény határértéke egy pontban egyenlő ennek a függvénynek az értékével egy adott pontban.

Így egy függvény egy pontban folytonos a függvény folytonosságának meghatározása szerint egy pontban.

Szokás szerint kutatás után rajzunkat átvisszük a végleges változatba.

Válasz: a függvény a pontokban folytonos.

Kérjük, vegye figyelembe, hogy abban az esetben nem kérdeztünk semmit a teljes függvény tanulmányozásáról a folytonosság érdekében, és jó matematikai formának tekinthető a megfogalmazása. pontos és világos a választ a feltett kérdésre. Egyébként, ha a feltételek nem követelik meg, hogy grafikont készíts, akkor minden jogod megvan, hogy ne építsd (bár később a tanár rákényszeríthet erre).

Egy kis matematikai „nyelvforgató” a megoldáshoz:

7. példa

Adott egy függvény . Vizsgáljuk meg a pontokban a folytonosság függvényét. Osztályozza a töréspontokat, ha vannak. Hajtsa végre a rajzot.

Próbáld meg helyesen "kiejteni" az összes "szót" =) És rajzold meg pontosabban a grafikont, pontosság, nem lesz mindenhol felesleges;-)

Ahogy emlékszel, javasoltam, hogy azonnal fejezd be a rajzot vázlatként, de időnként találkozol olyan példákkal, ahol nem tudod azonnal kitalálni, hogy néz ki a grafikon. Ezért bizonyos esetekben előnyös, ha először egyoldalú határokat találunk, és csak ezután, a tanulmány alapján ábrázoljuk az ágakat. Az utolsó két példában egy technikát is megtanulunk néhány egyoldalú határérték kiszámítására:

8. példa

Vizsgálja meg a folytonossági függvényt, és készítse el sematikus gráfját.

Megoldás: a rossz pontok nyilvánvalóak: (nullára csökkenti a kitevő nevezőjét) és (nullára csökkenti a teljes tört nevezőjét). Nem világos, hogy néz ki ennek a függvénynek a grafikonja, ami azt jelenti, hogy jobb, ha először kutatást végez.

Egy függvényt folytonosnak mondunk egy x0 pontban, ha f(x) f(x0)-ra, mint x x0-ra. Ebben az esetben f(x) - A = f(x) - f(x0) = ∆f. Ha egy f függvény egy bizonyos A intervallum minden pontjában folytonos, akkor ez a függvény folytonos lesz a teljes A intervallumon. Magát az A intervallumot pedig ebben az esetben hívjuk. folytonossági rés függvények f.

Az iskolai matematika tanfolyamon tanult folytonos függvények grafikonja „anélkül rajzolható meg, hogy felemelné a ceruzát a papírról”, mivel ez egy folytonos vonal. Ha valamely (a;b) intervallumon az f függvény folytonos és nem tűnik el, akkor ezen az intervallumon állandó előjelet fog tartani.

Ez a tulajdonság nagyon könnyen érthető. Az ökör tengelye felett elhelyezkedő függvénynek plusz, az ökör tengelye alatti függvénynek mínuszjele van. Ha a függvényvonal nem metszi az Ox tengelyt (a függvény nulla az Ox tengelyen), akkor nyilvánvalóan nem fogja megváltoztatni az előjelét.

Intervallum módszer

A függvények folytonossági tulajdonságainak egyik szembetűnő alkalmazása az intervallum-módszer, amely egy változó egyenlőtlenségeinek megoldására szolgál. Legyen valamilyen függvény folytonos az A intervallumon, és tűnjön el az ehhez az intervallumhoz tartozó véges számú pontban.

A fent megadott tulajdonságot használva ezek a pontok a teljes A intervallumot olyan intervallumokra osztják, amelyekben a függvény megtartja előjelét. Az összes intervallum előjelének meghatározásához elegendő ismerni ezen intervallumok bármelyikének előjelét.

Példa egy nem folytonos függvényre

Eddig csak folyamatos függvényekkel találkoztunk. De vannak olyan függvények, amelyek nem folytonosak minden olyan ponton, ahol meghatározásra kerülnek. Például az f(x) = (x) függvény, ahol (x) az x szám tört része. Ennek grafikonja a következő ábrán látható.

Könnyen belátható, hogy a függvény folytonosságának fő tulajdonsága az x0 pontban, amely bármely egész számmal egyenlő, nem teljesül. Ugyanakkor az f(x) = (x) függvény folytonos minden más pontban, ahol meghatározásra került, kivéve azokat a pontokat, ahol x egyenlő egész számmal. A grafikonon az ilyen pontokat szúrt körök jelzik.

Folyamatos, de egy adott pontban nem differenciálható függvények

Vannak olyan függvények, amelyek definíciós tartományuk minden pontján folytonosak. Ugyanakkor bizonyos pontokon nem lesznek származékaik. Például az y=|x| függvény folytonos a teljes numerikus egyenes mentén, de nem differenciálható az x = 0 pontban. Az alábbiakban ennek a függvénynek a grafikonja látható.

Előző cikk: Mekkora a fénysebesség Következő cikk: Harmonikus rezgések Az oszcillációs frekvencia fizikai képlete