Keresse meg a 0 3p szakaszhoz tartozó egyenlet gyökereit! Trigonometrikus egyenletek megoldása, gyökválasztási módszerek adott intervallumon

a) Oldja meg az egyenletet: .

b) Keresse meg ennek az egyenletnek a szegmenshez tartozó összes gyökerét!

A probléma megoldása

Ez a lecke egy trigonometrikus egyenlet megoldásának példáját tárgyalja, amely példaként használható C1 típusú feladatok megoldására a matematika egységes államvizsgára való felkészülés során.

Először is meg kell határozni a funkció hatókörét - az argumentum összes érvényes értéke. Ezután a megoldás során a trigonometrikus szinuszfüggvényt a redukciós képlet segítségével koszinuszra alakítjuk. Ezután az egyenlet összes tagja átkerül a bal oldalára, ahol a közös tényezőt a zárójelekből kivesszük. Minden tényező egyenlő nullával, ami lehetővé teszi az egyenlet gyökereinek meghatározását. Ezután a fordulatok módszerével meghatározzuk az adott szegmenshez tartozó gyökereket. Ehhez a megszerkesztett egységkörön egy adott szakasz bal szélétől jobbra egy kanyart jelölünk. Ezután az egységkörön talált gyökereket szakaszokkal összekötjük a középpontjával, és meghatározzuk azokat a pontokat, ahol ezek a szakaszok metszik a fordulatot. Ezek a metszéspontok jelentik a kívánt választ a probléma második részére.

Problémájára részletes megoldást rendelhet!!!

A trigonometrikus függvény (`sin x, cos x, tan x` vagy `ctg x`) előjele alatt ismeretlent tartalmazó egyenlőséget trigonometrikus egyenletnek nevezzük, és ezek képleteit vizsgáljuk meg a továbbiakban.

A legegyszerűbb egyenletek a `sin x=a, cos x=a, tg x=a, ctg x=a`, ahol `x` a keresendő szög, `a` tetszőleges szám. Írjuk fel mindegyikhez a gyökképleteket.

1. `sin x=a` egyenlet.

Az `|a|>1` esetén nincs megoldás.

Amikor `|a| A \leq 1` végtelen számú megoldást tartalmaz.

Gyökképlet: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. "cos x=a" egyenlet

Az `|a|>1` - mint a szinusz esetében - nincs megoldása valós számok között.

Amikor `|a| A \leq 1` végtelen számú megoldást tartalmaz.

Gyökképlet: `x=\pm arccos a + 2\pi n, n \in Z`

Szinusz és koszinusz speciális esetei grafikonokban.

3. "tg x=a" egyenlet

Végtelen számú megoldása van az "a" bármely értékére.

Gyökérképlet: `x=arctg a + \pi n, n \in Z`

4. `ctg x=a` egyenlet

Ezenkívül végtelen számú megoldása van az "a" bármely értékére.

Gyökérképlet: `x=arcctg a + \pi n, n \in Z`

A táblázatban szereplő trigonometrikus egyenletek gyökereinek képletei

A szinuszhoz:
A koszinuszhoz:
Érintő és kotangens esetén:
Képletek inverz trigonometrikus függvényeket tartalmazó egyenletek megoldására:

Trigonometrikus egyenletek megoldási módszerei

Bármely trigonometrikus egyenlet megoldása két lépésből áll:

• a legegyszerűbbre való átalakítás segítségével;
• oldja meg a fent leírt gyökképletek és táblázatok segítségével kapott legegyszerűbb egyenletet.

Nézzük meg a fő megoldási módszereket példákon keresztül.

Algebrai módszer.

Ez a módszer magában foglalja egy változó lecserélését és egyenlőségbe való behelyettesítését.

Példa. Oldja meg az egyenletet: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0,

cserélje ki: `cos(x+\frac \pi 6)=y, majd `2y^2-3y+1=0`,

megtaláljuk a gyökereket: `y_1=1, y_2=1/2`, amiből két eset következik:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Válasz: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktorizáció.

Példa. Oldja meg az egyenletet: `sin x+cos x=1`.

Megoldás. Mozgassuk az egyenlőség összes tagját balra: `sin x+cos x-1=0`. Használatával a bal oldalt transzformáljuk és faktorizáljuk:

"sin x - 2sin^2 x/2=0",

"2sin x/2 cos x/2-2sin^2 x/2=0",

"2sin x/2 (cos x/2-sin x/2)=0",

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. „cos x/2-sin x/2=0”, „tg x/2=1”, „x/2=arctg 1+ \pi n”, „x/2=\pi/4+ \pi n” , `x_2=\pi/2+ 2\pi n`.

Válasz: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Redukálás homogén egyenletre

Először is le kell redukálnia ezt a trigonometrikus egyenletet a két alak egyikére:

`a sin x+b cos x=0` (elsőfokú homogén egyenlet) vagy `a sin^2 x + b sin x cos x +c cos^2 x=0` (másodfokú homogén egyenlet).

Ezután ossza el mindkét részt `cos x \ne 0` -val - az első esetben, és "cos^2 x \ne 0" - a második esetben. Egyenleteket kapunk a `tg x`-re: `a tg x+b=0` és `a tg^2 x + b tg x +c =0`, amelyeket ismert módszerekkel kell megoldani.

Példa. Oldja meg az egyenletet: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Megoldás. Írjuk a jobb oldalt a következőképpen: `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Ez egy homogén másodfokú trigonometrikus egyenlet, bal és jobb oldalát elosztjuk `cos^2 x \ne 0`-val, így kapjuk:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0

`tg^2 x+tg x — 2=0`. Vezessük be a `tg x=t` helyettesítést, ami `t^2 + t - 2=0`-t eredményez. Ennek az egyenletnek a gyöke: `t_1=-2` és `t_2=1`. Akkor:

1. „tg x=-2”, „x_1=arctg (-2)+\pi n”, „n \in Z”
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

Válasz. `x_1=arctg (-2)+\pi n`, `n \in Z, `x_2=\pi/4+\pi n`, `n \in Z`.

Áttérés félszögre

Példa. Oldja meg az egyenletet: "11 sin x - 2 cos x = 10".

Megoldás. Alkalmazzuk a kettős szögképleteket, aminek eredménye: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

"4 tg^2 x/2 – 11 tg x/2 +6=0".

A fent leírt algebrai módszert alkalmazva a következőket kapjuk:

1. „tg x/2=2”, „x_1=2 arctg 2+2\pi n”, „n \in Z”,
2. „tg x/2=3/4”, „x_2=arctg 3/4+2\pi n”, „n \in Z”.

Válasz. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Segédszög bevezetése

Az „a sin x + b cos x =c” trigonometrikus egyenletben, ahol a,b,c együtthatók, x pedig egy változó, mindkét oldalt ossza el „sqrt (a^2+b^2)”-vel:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))".

A bal oldali együtthatók szinusz és koszinusz tulajdonságaival rendelkeznek, vagyis négyzeteinek összege 1, moduljaik pedig nem nagyobbak 1-nél. Jelöljük őket a következőképpen: `\frac a(sqrt (a^2) +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, akkor:

`cos \varphi sin x + sin \varphi cos x =C`.

Nézzük meg közelebbről a következő példát:

Példa. Oldja meg az egyenletet: `3 sin x+4 cos x=2`.

Megoldás. Az egyenlőség mindkét oldalát elosztjuk `sqrt (3^2+4^2)-vel, így kapjuk:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))".

"3/5 sin x+4/5 cos x=2/5".

Jelöljük `3/5 = cos \varphi` , `4/5=sin \varphi`. Mivel a `sin \varphi>0`, `cos \varphi>0`, akkor a `\varphi=arcsin 4/5`-t vesszük segédszögnek. Ezután az egyenlőségünket a következő formában írjuk fel:

`cos \varphi sin x+sin \varphi cos x=2/5`

A szinusz szögösszegének képletét alkalmazva egyenlőségünket a következő formában írjuk fel:

"sin (x+\varphi)=2/5",

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Válasz. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Törtracionális trigonometrikus egyenletek

Ezek olyan tört egyenlőségek, amelyek számlálói és nevezői trigonometrikus függvényeket tartalmaznak.

Példa. Oldja meg az egyenletet. `\frac (sin x)(1+cos x)=1-cos x.

Megoldás. Szorozd meg és oszd el az egyenlőség jobb oldalát "(1+cos x)"-vel. Ennek eredményeként a következőket kapjuk:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0

"\frac (sin x-sin^2 x)(1+cos x)=0".

Figyelembe véve, hogy a nevező nem lehet egyenlő nullával, a következőt kapjuk: `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Tegyük egyenlővé a tört számlálóját nullával: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Ezután `sin x=0` vagy `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Tekintettel arra, hogy ` x \ne \pi+2\pi n, n \in Z`, a megoldások: `x=2\pi n, n \in Z` és `x=\pi /2+2\pi n` , `n \in Z`.

Válasz. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

A trigonometriát, és különösen a trigonometrikus egyenleteket a geometria, a fizika és a mérnöki tudomány szinte minden területén használják. A tanulás a 10. osztályban kezdődik, az egységes államvizsgához mindig vannak feladatok, ezért próbálja meg emlékezni a trigonometrikus egyenletek összes képletére - ezek biztosan hasznosak lesznek az Ön számára!

Azonban még csak memorizálni sem kell őket, a lényeg az, hogy megértsük a lényeget és le tudjuk vezetni. Nem olyan nehéz, mint amilyennek látszik. Győződjön meg Ön is a videó megtekintésével.

Ebben a cikkben 2 módszert próbálok megmagyarázni gyökök kiválasztása egy trigonometrikus egyenletben: egyenlőtlenségek és a trigonometrikus kör használata. Térjünk át egy szemléltető példára, és rájövünk, hogyan működnek a dolgok.

A) Oldja meg az sqrt(2)cos^2x=sin(Pi/2+x) egyenletet
b) Határozzuk meg ennek az egyenletnek a [-7Pi/2 intervallumhoz tartozó gyökét; -2Pi]

Oldjuk meg az a) pontot.

Használjuk a szinusz sin(Pi/2+x) = cos(x) redukciós képletét

Sqrt(2)cos^2x = cosx

Sqrt(2)cos^2x - cosx = 0

Cosx(sqrt(2)cosx - 1) = 0

X1 = Pi/2 + Pin, n ∈ Z

Sqrt(2)cosx - 1 = 0

Cosx = 1/sqrt(2)

Cosx = sqrt(2)/2

X2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

X2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Oldjuk meg a b pontot.

1) Gyökök kiválasztása egyenlőtlenségek segítségével

Itt minden egyszerűen történik, a kapott gyököket behelyettesítjük a nekünk adott intervallumba [-7Pi/2; -2Pi], keresse meg n egész értékét.

7Pi/2 kisebb vagy egyenlő, mint Pi/2 + Pin kisebb vagy egyenlő, mint -2Pi

Azonnal mindent elosztunk Pi-vel

7/2 kisebb vagy egyenlő, mint 1/2 + n kisebb vagy egyenlő, mint -2

7/2 - 1/2 kisebb vagy egyenlő, mint n kisebb vagy egyenlő, mint -2 - 1/2

4 kisebb vagy egyenlő, mint n kisebb vagy egyenlő, mint -5/2

Az n egész szám ebben az intervallumban -4 és -3. Ez azt jelenti, hogy az ehhez az intervallumhoz tartozó gyökök Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Hasonlóképpen készítünk még két egyenlőtlenséget

7Pi/2 kisebb vagy egyenlő, mint Pi/4 + 2Pin kisebb vagy egyenlő, mint -2Pi
-15/8 kisebb vagy egyenlő, mint n kisebb vagy egyenlő, mint -9/8

Ebben az intervallumban nincs egész n

7Pi/2 kisebb vagy egyenlő, mint -Pi/4 + 2Pin kisebb vagy egyenlő, mint -2Pi
-13/8 kisebb vagy egyenlő, mint n kisebb vagy egyenlő, mint -7/8

Ebben az intervallumban egy n egész szám -1. Ez azt jelenti, hogy a kiválasztott gyök ezen az intervallumon -Pi/4 + 2Pi*(-1) = -9Pi/4.

Tehát a válasz a b pontban: -7Pi/2, -5Pi/2, -9Pi/4

2) Gyökerek kiválasztása trigonometrikus kör segítségével

A módszer használatához meg kell értened, hogyan működik ez a kör. Megpróbálom egyszerű nyelven elmagyarázni, hogyan értem ezt. Szerintem az iskolákban, algebra órán sokszor okos szavakkal fejtették ki ezt a témát a tanártól, a tankönyvekben bonyolult megfogalmazások voltak. Én személy szerint ezt egy végtelen sokszor körbejárható körként értem, ez azzal magyarázható, hogy a szinusz és a koszinusz függvények periodikusak.

Menjünk körbe az óramutató járásával ellentétes irányba

Kerüljünk 2-szer az óramutató járásával ellentétes irányba

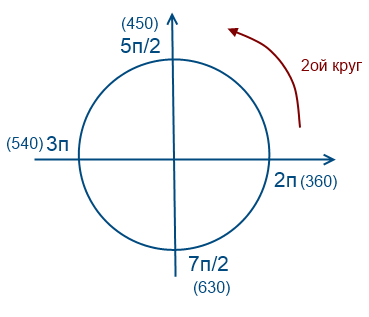
Kerüljünk 1-szer az óramutató járásával megegyezően (az értékek negatívak lesznek)

Térjünk vissza kérdésünkre, gyököket kell kiválasztanunk a [-7Pi/2; -2Pi]

A -7Pi/2 és -2Pi számok eléréséhez kétszer kell megkerülni a kört az óramutató járásával ellentétes irányba. Ahhoz, hogy megtaláljuk az egyenlet gyökereit ezen az intervallumon, meg kell becsülnünk és be kell cserélnünk.

Tekintsük x = Pi/2 + Pin. Körülbelül mi legyen n, hogy x valahol ebben a tartományban legyen? Behelyettesítjük mondjuk -2-t, Pi/2 - 2Pi = -3Pi/2-t kapunk, nyilván ez nincs benne az intervallumunkban, tehát -3-nál kevesebbet veszünk, Pi/2 - 3Pi = -5Pi/2, ez alkalmas, próbáljuk újra -4 , Pi/2 - 4Pi = -7Pi/2, szintén megfelelő.

Hasonlóan érvelve a Pi/4 + 2Pin és -Pi/4 + 2Pin esetén, találunk még egy gyökér -9Pi/4.

Két módszer összehasonlítása.

Az első módszer (egyenlőtlenségeket használva) sokkal megbízhatóbb és sokkal könnyebben érthető, de ha komolyan foglalkozik a trigonometrikus körrel és a második kiválasztási módszerrel, akkor a gyökök kiválasztása sokkal gyorsabb lesz, körülbelül 15 percet takaríthat meg a vizsgán. .

Az óra célja:

A) erősíti az egyszerű trigonometrikus egyenletek megoldásának képességét;

b) tanítsa meg a trigonometrikus egyenletek gyökeinek kiválasztását egy adott intervallumból

Az órák alatt.

a) Házi feladat ellenőrzése: emelt szintű házi feladatot kap az osztály - oldjon meg egy egyenletet és találjon módot a gyökök kiválasztására egy adott intervallumból.

1) cos x= -0,5, ahol xI [- ]. Válasz:.

2) bűn x= , ahol xI . Válasz: ; .

3) cos 2 x= -, ahol xI. Válasz:

A tanulók felírják a táblára a megoldást, egyesek grafikon segítségével, mások kijelölési módszerrel.

Ebben az időben osztály szóban működik.

Keresse meg a kifejezés jelentését:

a) tg – sin + cos + sin. Válasz: 1.

b) 2 arccos 0 + 3 arccos 1. Válasz: ?

c) arcsin + arcsin. Válasz:.

d) 5 arctg (-) – arccos (-). Válasz:-.

- Ellenőrizzük a házi feladatot, nyissuk ki a füzeteket a házi feladattal.

Néhányan a kiválasztási módszerrel, mások a grafikon segítségével találták meg a megoldást.

2. Következtetések ezeknek a feladatoknak a megoldási módjairól és a probléma megfogalmazása, azaz az óra témájának és céljának közlése.

– a) Kiválasztással nehéz megoldani, ha nagy intervallum adott.

– b) A grafikus módszer nem ad pontos eredményt, ellenőrzést igényel, és sok időt vesz igénybe.

- Ezért kell lennie még legalább egy módszernek, a leguniverzálisabbnak - próbáljuk meg megtalálni. Szóval mit fogunk csinálni ma az órán? (Tanulja meg, hogyan kell kiválasztani a trigonometrikus egyenlet gyökereit egy adott intervallumon.)

– 1. példa (A tanuló a táblához megy)

kötözősaláta x= -0,5, ahol xI [- ].

Kérdés: Mi határozza meg erre a feladatra a választ? (Az egyenlet általános megoldásából. Írjuk fel a megoldást általános formában). A megoldás fel van írva a táblára

x = + 2?k, ahol k R.

– Írjuk fel ezt a megoldást halmaz formájában:

– Ön szerint a megoldás milyen jelölésében célszerű az intervallumon gyököket választani? (a második bejegyzésből). De ez megint egy kiválasztási módszer. Mit kell tudnunk a helyes válaszhoz? (Ismernie kell a k értékeit).

(Készítsünk matematikai modellt k megtalálásához).

Következtetés: Egy adott intervallum gyökeinek kiválasztásához trigonometrikus egyenlet megoldása során a következőket kell tennie:

1. alakú egyenlet megoldására sin x = a, cos x = a Kényelmesebb az egyenlet gyökereit két gyöksorozatként felírni.
2. alakú egyenletek megoldására tan x = a, ctg x = aírja le a gyökök általános képletét.
3. minden megoldáshoz készítsünk matematikai modellt kettős egyenlőtlenség formájában, és keressük meg a k vagy n paraméter egész értékét.
4. cserélje ki ezeket az értékeket a gyökérképletbe, és számítsa ki őket.

Oldja meg a 2. és 3. példát a házi feladatból a kapott algoritmus segítségével. Egyszerre két diák dolgozik a táblánál, majd a munka ellenőrzése következik.