Két vagy három, egymásra merőleges, közös origóval (koordináták origójával) és közös hosszegységgel metsző tengelyből álló rendezett rendszert ún. derékszögű derékszögű koordinátarendszer .

Általános derékszögű koordinátarendszer (affin koordinátarendszer) nem feltétlenül tartalmazhat merőleges tengelyeket. Rene Descartes (1596-1662) francia matematikus tiszteletére éppen egy olyan koordinátarendszert neveznek el, amelyben minden tengelyen közös hosszegységet mérnek, és a tengelyek egyenesek.

Derékszögű derékszögű koordinátarendszer egy síkon két tengelye és derékszögű derékszögű koordinátarendszer a térben - három tengely. A síkon vagy a térben minden pontot koordináták rendezett halmaza határoz meg - a koordinátarendszer hosszegységének megfelelő számok.

Vegyük észre, hogy a definícióból következik, hogy van egy derékszögű koordinátarendszer egy egyenesen, azaz egy dimenzióban. A derékszögű koordináták bevezetése egy egyenesre az egyik módja annak, hogy az egyenes bármely pontja jól meghatározott valós számhoz, azaz koordinátához rendelhető.

A koordináta-módszer, amely Rene Descartes munkáiban merült fel, az egész matematika forradalmi átstrukturálását jelentette. Lehetővé vált az algebrai egyenletek (vagy egyenlőtlenségek) geometriai képek (grafikonok) formájában történő értelmezése, és fordítva, a geometriai problémák megoldásának keresése analitikus képletek és egyenletrendszerek segítségével. Igen, egyenlőtlenség z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOyés e sík felett helyezkedik el 3 egységgel.

A derékszögű koordinátarendszer segítségével egy adott görbe pontjának tagsága megfelel annak, hogy a számok xÉs y kielégíteni valamilyen egyenletet. Így a kör azon pontjának koordinátái, amelynek középpontja egy adott pontban van ( a; b) teljesítik az egyenletet (x - a)² + ( y - b)² = R² .

Derékszögű derékszögű koordinátarendszer egy síkon

Egy síkon két egymásra merőleges tengely alakul ki, amelyeknek közös origója és azonos léptékegysége van Derékszögű derékszögű koordinátarendszer a síkon . Ezen tengelyek egyikét tengelynek nevezzük Ökör, vagy x tengely , a másik - a tengely Oy, vagy y tengely . Ezeket a tengelyeket koordinátatengelyeknek is nevezik. Jelöljük azzal MxÉs My illetve egy tetszőleges pont vetülete M a tengelyen ÖkörÉs Oy. Hogyan szerezzünk előrejelzéseket? Menjünk a lényegen M Ökör. Ez az egyenes metszi a tengelyt Ökör azon a ponton Mx. Menjünk a lényegen M tengelyre merőleges egyenes Oy. Ez az egyenes metszi a tengelyt Oy azon a ponton My. Ez az alábbi képen látható.

xÉs y pontokat M ennek megfelelően hívjuk az irányított szegmensek értékeit OMxÉs OMy. Ezen irányított szegmensek értéke ennek megfelelően kerül kiszámításra x = x0 - 0 És y = y0 - 0 . Derékszögű koordináták xÉs y pontokat M abszcissza És ordináta . Az a tény, hogy a lényeg M koordinátái vannak xÉs y, a következőképpen jelöljük: M(x, y) .

A koordinátatengelyek négy részre osztják a síkot negyedkör , melynek számozása az alábbi ábrán látható. Megmutatja a pontok koordinátáinak jeleinek elrendezését is, attól függően, hogy hol helyezkednek el egy adott negyedben.

A síkon a derékszögű derékszögű koordináták mellett gyakran figyelembe veszik a poláris koordináta-rendszert is. Az egyik koordinátarendszerből a másikba való átmenet módszeréről - a leckében poláris koordináta-rendszer .

Derékszögű derékszögű koordinátarendszer a térben

A térben a derékszögű koordinátákat a síkban lévő derékszögű koordinátákkal teljes analógiaként vezetjük be.

Három, egymásra merőleges tengely a térben (koordinátatengelyek), közös origóval Oés azonos léptékegységgel alkotják Derékszögű derékszögű koordinátarendszer a térben .

Ezen tengelyek egyikét tengelynek nevezzük Ökör, vagy x tengely , a másik - a tengely Oy, vagy y tengely , a harmadik - tengely Oz, vagy tengelyt alkalmazni . Hadd Mx, My Mz- tetszőleges pont vetületei M hely a tengelyen Ökör , OyÉs Oz illetőleg.

Menjünk át a lényegen M ÖkörÖkör azon a ponton Mx. Menjünk a lényegen M tengelyre merőleges sík Oy. Ez a sík metszi a tengelyt Oy azon a ponton My. Menjünk a lényegen M tengelyre merőleges sík Oz. Ez a sík metszi a tengelyt Oz azon a ponton Mz.

Derékszögű derékszögű koordináták x , yÉs z pontokat M ennek megfelelően hívjuk az irányított szegmensek értékeit OMx, OMyÉs OMz. Ezeknek az irányított szegmenseknek az értékeit ennek megfelelően számítjuk ki x = x0 - 0 , y = y0 - 0 És z = z0 - 0 .

Derékszögű koordináták x , yÉs z pontokat M ennek megfelelően hívják abszcissza , ordináta És alkalmazni .

A párban vett koordinátatengelyek koordinátasíkban helyezkednek el xOy , yOzÉs zOx .

Pontokkal kapcsolatos feladatok egy derékszögű koordinátarendszerben

1. példa

A(2; -3) ;

B(3; -1) ;

C(-5; 1) .

Keresse meg ezeknek a pontoknak az abszcissza tengelyre való vetületeinek koordinátáit.

Megoldás. A lecke elméleti részéből következően egy pontnak az abszcissza tengelyére való vetítése magán az abszcissza tengelyen található, vagyis a tengelyen Ökör, ezért van egy abszcisszája magának a pontnak az abszcisszájával, és van egy ordinátája (a tengely koordinátája Oy, amelyet az x tengely a 0) pontban metszi, ami egyenlő nullával. Így az x tengely pontjainak a következő koordinátáit kapjuk:

Ax(2;0);

Bx(3;0);

Cx (-5; 0).

2. példa A derékszögű koordinátarendszerben a pontok a síkon vannak megadva

A(-3; 2) ;

B(-5; 1) ;

C(3; -2) .

Keresse meg ezeknek a pontoknak az ordináta tengelyre való vetületeinek koordinátáit.

Megoldás. A lecke elméleti részéből az következik, hogy egy pont ordináta tengelyre vetítése magán az ordináta tengelyen, azaz a tengelyen található. Oy, ezért van egy ordinátája megegyezik magának a pont ordinátájával, és van egy abszcisszája (koordinátája a tengelyen Ökör, amelyet az ordináta tengelye a 0) pontban metszi, ami egyenlő nullával. Tehát ezeknek a pontoknak a következő koordinátáit kapjuk az ordináta tengelyen:

Ay(0;2);

By(0;1);

Cy(0;-2).

3. példa A derékszögű koordinátarendszerben a pontok a síkon vannak megadva

A(2; 3) ;

B(-3; 2) ;

C(-1; -1) .

Ökör .

Ökör Ökör Ökör, az adott pont abszcisszája lesz, és az ordináta abszolút értékében egyenlő az adott pont ordinátájával, és ellenkező előjelű. Így a tengelyhez képest ezekre a pontokra szimmetrikus pontok alábbi koordinátáit kapjuk Ökör :

A"(2; -3) ;

B"(-3; -2) ;

C"(-1; 1) .

Oldja meg a problémákat a derékszögű koordinátarendszer segítségével, majd nézze meg a megoldásokat

4. példa Határozza meg, mely negyedekben (negyedek, rajzolás kvadránsokkal - a „Téglalap derékszögű koordinátarendszer egy síkon” bekezdés végén) helyezhető el egy pont M(x; y) , Ha

1) xy > 0 ;

2) xy < 0 ;

3) x − y = 0 ;

4) x + y = 0 ;

5) x + y > 0 ;

6) x + y < 0 ;

7) x − y > 0 ;

8) x − y < 0 .

5. példa A derékszögű koordinátarendszerben a pontok a síkon vannak megadva

A(-2; 5) ;

B(3; -5) ;

C(a; b) .

Keresse meg az ezekre a pontokra szimmetrikus pontok koordinátáit a tengelyhez képest Oy .

Folytassuk a problémák közös megoldását

6. példa. A derékszögű koordinátarendszerben a pontok a síkon vannak megadva

A(-1; 2) ;

B(3; -1) ;

C(-2; -2) .

Keresse meg az ezekre a pontokra szimmetrikus pontok koordinátáit a tengelyhez képest Oy .

Megoldás. Forgassa el 180 fokkal a tengely körül Oy irányszegmens a tengelytől Oy eddig a pontig. Az ábrán, ahol a sík kvadránsai vannak feltüntetve, azt látjuk, hogy az adott pontra a tengelyhez képest szimmetrikus pont Oy, ugyanaz lesz az ordinátája, mint az adott pontnak, és egy abszcisszája abszolút értékben megegyezik az adott pont abszcisszájával, és ellentétes előjellel. Így a tengelyhez képest ezekre a pontokra szimmetrikus pontok alábbi koordinátáit kapjuk Oy :

A"(1; 2) ;

B"(-3; -1) ;

C"(2; -2) .

7. példa. A derékszögű koordinátarendszerben a pontok a síkon vannak megadva

A(3; 3) ;

B(2; -4) ;

C(-2; 1) .

Határozzuk meg az origóhoz képest ezekre a pontokra szimmetrikus pontok koordinátáit!

Megoldás. Az origótól az adott pontig tartó irányított szakaszt 180 fokkal elforgatjuk az origó körül. Az ábrán, ahol a sík kvadránsai vannak feltüntetve, azt látjuk, hogy az adott pontra a koordináták origójához képest szimmetrikus pontnak az abszcisszája és az ordinátája abszolút értékben megegyezik az adott pont abszcisszájával és ordinátájával, de ellentétes előjelben. Így az origóhoz képest ezekre a pontokra szimmetrikus pontok alábbi koordinátáit kapjuk:

A"(-3; -3) ;

B"(-2; 4) ;

C(2; -1) .

8. példa.

A(4; 3; 5) ;

B(-3; 2; 1) ;

C(2; -3; 0) .

Keresse meg ezen pontok vetületeinek koordinátáit:

1) repülőn Oxy ;

2) repülőn Oxz ;

3) a repülőre Oyz ;

4) az abszcissza tengelyen;

5) az ordináta tengelyen;

6) az alkalmazási tengelyen.

1) Egy pont síkra vetítése Oxy magán ezen a síkon helyezkedik el, ezért az abszcisszája és az ordinátája megegyezik egy adott pont abszcisszájával és ordinátájával, és az applikátuma nullával egyenlő. Így ezeknek a pontoknak a vetületeinek a következő koordinátáit kapjuk Oxy :

Axy (4; 3; 0);

Bxy (-3; 2; 0);

Cxy(2;-3;0).

2) Egy pont síkra vetítése Oxz magán ezen a síkon helyezkedik el, ezért az abszcisszája és az applikációja megegyezik egy adott pont abszcisszájával és applikációjával, és az ordinátája egyenlő nullával. Így ezeknek a pontoknak a vetületeinek a következő koordinátáit kapjuk Oxz :

Axz (4; 0; 5);

Bxz (-3; 0; 1);

Cxz (2; 0; 0).

3) Egy pont síkra vetítése Oyz magán ezen a síkon helyezkedik el, ezért az ordinátája és az applikációja egyenlő egy adott pont ordinátájával és applikációjával, az abszcisszája pedig nullával egyenlő. Így ezeknek a pontoknak a vetületeinek a következő koordinátáit kapjuk Oyz :

Ayz(0; 3; 5);

Byz (0; 2; 1);

Cyz (0; -3; 0).

4) A lecke elméleti részéből következően egy pontnak az abszcissza tengelyére vetítése magán az abszcissza tengelyen található, vagyis a tengelyen Ökör, ezért az abszcisszája megegyezik magának a pontnak abszcisszájával, a vetület ordinátája és applikátuma pedig nulla (mivel az ordináta és az applikációs tengely a 0 pontban metszi az abszcisszát). Ezeknek a pontoknak az abszcissza tengelyre való vetületeinek a következő koordinátáit kapjuk:

Ax (4; 0; 0);

Bx (-3; 0; 0);

Cx(2;0;0).

5) Egy pont ordináta tengelyre vetítése magán az ordináta tengelyen található, vagyis a tengelyen Oy, és ezért ordinátája megegyezik magának a pontnak az ordinátájával, és a vetítés abszcissza és applikátuma nulla (mivel az abszcissza és az applikációs tengely a 0 pontban metszi az ordináta tengelyét). Ezeknek a pontoknak az ordináta tengelyre való vetületeinek a következő koordinátáit kapjuk:

Ay(0; 3; 0);

By (0; 2; 0);

Cy(0;-3;0).

6) Egy pont vetülete az alkalmazási tengelyre magán az alkalmazási tengelyen, azaz a tengelyen található Oz, és ezért magának a pontnak az applikátumával egyenlő, és a vetítés abszcissza és ordinátája egyenlő nullával (mivel az abszcissza és az ordináta tengelye a 0 pontban metszi az applikációs tengelyt). Ezeknek a pontoknak az alkalmazási tengelyre való vetületeinek a következő koordinátáit kapjuk:

Az (0; 0; 5);

Bz (0; 0; 1);

Cz(0; 0; 0).

9. példa. A derékszögű koordinátarendszerben a pontok térben vannak megadva

A(2; 3; 1) ;

B(5; -3; 2) ;

C(-3; 2; -1) .

Határozzuk meg az ezekre a pontokra szimmetrikus pontok koordinátáit:

1) repülőgép Oxy ;

2) repülőgépek Oxz ;

3) repülőgépek Oyz ;

4) abszcissza tengelyek;

5) ordináta tengelyek;

6) alkalmazza a tengelyeket;

7) koordináták origója.

1) „Mozgassa” a pontot a tengely másik oldalán Oxy Oxy, az abszcisszája és az ordinátája megegyezik egy adott pont abszcisszájával és ordinátájával, valamint egy adott pont aplikátjával nagyságrendileg megegyező, de az előjelben ellentétes applikációja lesz. Tehát a következő koordinátákat kapjuk az adatokra szimmetrikusan a síkhoz képest Oxy :

A"(2; 3; -1) ;

B"(5; -3; -2) ;

C"(-3; 2; 1) .

2) „Mozgassa” a pontot a tengely másik oldalán Oxz ugyanarra a távolságra. A koordinátateret ábrázoló ábrán azt látjuk, hogy egy adott pontra a tengelyhez képest szimmetrikus pont Oxz, az abszcisszája és az applikációja megegyezik egy adott pont abszcisszájával és applikációjával, valamint egy adott pont ordinátájával nagyságrendileg megegyező, de előjelben ellentétes ordinátája. Tehát a következő koordinátákat kapjuk az adatokra szimmetrikusan a síkhoz képest Oxz :

A"(2; -3; 1) ;

B"(5; 3; 2) ;

C"(-3; -2; -1) .

3) „Mozgassa” a pontot a tengely másik oldalán Oyz ugyanarra a távolságra. A koordinátateret ábrázoló ábrán azt látjuk, hogy egy adott pontra a tengelyhez képest szimmetrikus pont Oyz, egy adott pont ordinátájával és aplikátjával egyenlő ordinátája és aplikátja, valamint egy adott pont abszcisszájával egyenlő értékű, de előjelben ellentétes abszcisszája lesz. Tehát a következő koordinátákat kapjuk az adatokra szimmetrikusan a síkhoz képest Oyz :

A"(-2; 3; 1) ;

B"(-5; -3; 2) ;

C"(3; 2; -1) .

A sík szimmetrikus pontjaihoz és a síkokhoz viszonyított adatokra szimmetrikus térbeli pontokhoz hasonlóan megjegyezzük, hogy a térbeli derékszögű koordinátarendszer valamely tengelyéhez viszonyított szimmetria esetén a tengelyen lévő koordináta a térbeli koordinátarendszerhez képest. amelynek szimmetriája adott, megtartja előjelét, a másik két tengely koordinátái pedig abszolút értékben megegyeznek egy adott pont koordinátáival, de ellentétes előjellel.

4) Az abszcissza megtartja jelét, de az ordináta és az applikátum jeleket vált. Így az adatokra szimmetrikus pontok alábbi koordinátáit kapjuk az abszcissza tengelyhez viszonyítva:

A"(2; -3; -1) ;

B"(5; 3; -2) ;

C"(-3; -2; 1) .

5) Az ordináta megtartja előjelét, de az abszcissza és az applikátum előjelet vált. Tehát az adatokkal szimmetrikus pontok alábbi koordinátáit kapjuk az ordinátatengelyhez képest:

A"(-2; 3; -1) ;

B"(-5; -3; -2) ;

C"(3; 2; 1) .

6) A kérvény megtartja a jelét, de az abszcissza és az ordináta jelet vált. Így a következő pontok koordinátáit kapjuk, amelyek szimmetrikusak az adatokkal az alkalmazási tengelyhez képest:

A"(-2; -3; 1) ;

B"(-5; 3; 2) ;

C"(3; -2; -1) .

7) A szimmetriával analóg módon egy síkon lévő pontok esetén a koordináták origójára vonatkozó szimmetria esetén egy adott pontra szimmetrikus pont összes koordinátája abszolút értékben egyenlő egy adott pont koordinátáival, de velük szemben jelben. Így az adatokkal szimmetrikus pontok alábbi koordinátáit kapjuk az origóhoz képest.

Egy síkon egy téglalap alakú koordinátarendszert két egymásra merőleges X’X és Y’Y koordinátatengely alkot. A koordinátatengelyek az O pontban metszik egymást, amelyet origónak nevezünk, minden tengelyen egy pozitív irányt választunk. az óramutató járásával ellentétes irányban 90°-kal, pozitív iránya egybeesik az Y'Y tengely pozitív irányával. Az X'X és Y'Y koordinátatengelyek által alkotott négy szöget (I, II, III, IV) koordinátaszögeknek nevezzük (lásd 1. ábra).

Az A pont helyzetét a síkon két x és y koordináta határozza meg. Az x koordináta egyenlő az OB szakasz hosszával, az y koordináta egyenlő az OC szakasz hosszával a kiválasztott mértékegységekben. Az OB és OC szakaszokat az A pontból az Y'Y és X'X tengellyel párhuzamos vonalak határozzák meg. Az x koordinátát az A pont abszcisszájának, az y koordinátát az A pont ordinátájának nevezzük. A következőképpen írjuk fel: A(x, y).

Ha az A pont az I koordinátaszögben van, akkor az A pont pozitív abszcissza és ordináta. Ha az A pont a II koordinátaszögben van, akkor az A pontnak negatív abszcissza és pozitív ordinátája van. Ha az A pont a III koordinátaszögben van, akkor az A pont negatív abszcissza és ordináta. Ha az A pont a IV koordinátaszögben van, akkor az A pontnak pozitív abszcissza és negatív ordinátája van.

Téglalap alakú koordinátarendszer a térben három egymásra merőleges OX, OY és OZ koordinátatengely alkotja. A koordinátatengelyek az O pontban metszik egymást, amelyet origónak nevezünk, minden tengelyen kiválasztunk egy pozitív irányt, amelyet nyilak jelölnek, és a tengelyeken lévő szakaszok mértékegységét. A mértékegységek minden tengelyre azonosak. OX - abszcissza tengely, OY - ordináta tengely, OZ - applikációs tengely. A tengelyek pozitív irányát úgy választjuk meg, hogy ha az OX tengelyt az óramutató járásával ellentétes irányban 90°-kal elforgatjuk, akkor annak pozitív iránya egybeessen az OY tengely pozitív irányával, ha ezt az elfordulást az OZ tengely pozitív irányából figyeljük meg. Az ilyen koordinátarendszert jobbkezesnek nevezzük. Ha a jobb kéz hüvelykujját X iránynak, a mutatóujját Y iránynak, a középső ujját pedig Z iránynak vesszük, akkor jobb kéz koordinátarendszere jön létre. A bal kéz hasonló ujjai alkotják a bal oldali koordinátarendszert. Lehetetlen úgy kombinálni a jobb és bal koordinátarendszert, hogy a megfelelő tengelyek egybeessenek (lásd 2. ábra).

Az A pont helyzetét a térben három x, y és z koordináta határozza meg. Az x koordináta egyenlő az OB szakasz hosszával, az y koordináta az OC szakasz hossza, a z koordináta az OD szakasz hossza a kiválasztott mértékegységekben. Az OB, OC és OD szakaszokat az A pontból a YOZ, XOZ és XOY síkkal párhuzamos síkok határozzák meg. Az x koordinátát az A pont abszcisszájának, az y koordinátát az A pont ordinátájának, a z koordinátát az A pont alkalmazásának nevezzük. A következőképpen írjuk fel: A(a, b, c).

Orty

A téglalap alakú koordinátarendszert (bármilyen méretben) a koordinátatengelyekhez igazított egységvektorok halmaza is leírja. Az egységvektorok száma megegyezik a koordinátarendszer méretével, és mind merőlegesek egymásra.

Háromdimenziós esetben általában ilyen egységvektorokat jelölnek én j k vagy e x e y e z. Ebben az esetben jobbos koordinátarendszer esetén a következő képletek érvényesek a vektorok vektorszorzatával:

• [én j]=k ;
• [j k]=én ;
• [k én]=j .

Sztori

A téglalap alakú koordináta-rendszert először Rene Descartes vezette be 1637-ben „Discourse on Method” című munkájában. Ezért a téglalap alakú koordinátarendszert - Derékszögű koordinátarendszer. A geometriai objektumok leírásának koordinátamódszere az analitikus geometria kezdetét jelentette. Pierre Fermat is hozzájárult a koordináta-módszer kidolgozásához, de munkái először halála után jelentek meg. Descartes és Fermat csak a síkon alkalmazta a koordináta módszert.

A háromdimenziós tér koordináta-módszerét először Leonhard Euler alkalmazta már a 18. században.

Lásd még

Linkek

Wikimédia Alapítvány. 2010.

• Derékszögű koordinátarendszer
• Descartes fokozat

Nézze meg, mik a „derékszögű koordináták” más szótárakban:

KARTESINE KOORDINÁTÁK- (derékszögű koordinátarendszer) egy síkon vagy térben lévő koordinátarendszer, általában egymásra merőleges tengelyekkel és a tengelyek mentén egyenlő léptékekkel. R. Descartes nevéhez fűződik... Nagy enciklopédikus szótár

Derékszögű koordináták- Két egymásra merőleges tengelyből álló koordinátarendszer. Egy pont helyzetét egy ilyen rendszerben két szám segítségével határozzuk meg, amelyek meghatározzák a koordináta középpontjától való távolságot az egyes tengelyek mentén. Tájékoztató témák...... Műszaki fordítói útmutató

Derékszögű koordináták- (derékszögű koordinátarendszer), egy síkon vagy térben lévő koordinátarendszer, általában egymásra merőleges tengelyekkel és a tengelyek mentén egyenlő skálákkal. R. Descartes nevéhez fűződik... enciklopédikus szótár

Derékszögű koordináták- Dekarto koordinatės statusas T terület Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: engl. Derékszögű koordináták vok. kartesische Koordinaten, f… Penkiakalbis aiškinamasis metrologijos terminų žodynas

Derékszögű koordináták- Dekarto koordinatės statusas T terület fizika atitikmenys: engl. derékszögű koordináták; rács koordináták vok. kartesische Koordinaten, f rus. Derékszögű koordináták, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas

KARTESINE KOORDINÁTÁK- egy módszer a pontok helyzetének meghatározására egy síkon két rögzített, merőleges egyenes tengelytől való távolságuk alapján. Ez a fogalom már több mint kétezer évvel ezelőtti Arkhimédészben és Pergai Appologiszban, sőt az ókori egyiptomiaknál is megtalálható. Ez az első alkalom...... Matematikai Enciklopédia

KARTESINE KOORDINÁTÁK- Derékszögű koordinátarendszer [a franciákról kapta a nevét. filozófus és matematikus R. Descartes (R. Descartes; 1596 1650)], koordinátarendszer egy síkon vagy térben, általában egymásra merőleges tengelyekkel és egyenlő léptékekkel a téglalap alakú tengelyek mentén ... Nagy enciklopédikus politechnikai szótár

KARTESINE KOORDINÁTÁK- (derékszögű koordinátarendszer), egy síkon vagy térben lévő koordinátarendszer, amely általában egymásra merőleges tengelyekkel és a téglalap alakú tengelyek mentén egyenlő léptékekkel rendelkezik R. Descartesről elnevezett... Természettudomány. enciklopédikus szótár

KARTESINE KOORDINÁTÁK- A rendszer a csontokon található bármely pont pozícionálására két, derékszögben metsző tengelyhez képest. A René Descartes által kifejlesztett rendszer az adatok grafikus ábrázolásának szabványos módszereinek alapja lett. Vízszintes vonal… … Pszichológiai magyarázó szótár

Koordináták- Koordináták. A síkon (balra) és a térben (jobbra). KOORDINÁTÁK (a latin co szóból együtt és ordinatus rendezett), számok, amelyek meghatározzák egy pont helyzetét egy egyenesen, síkon, felületen, térben. A koordináták távolságok... Illusztrált enciklopédikus szótár

Kör egyenlete a koordinátasíkon

1. definíció. Számtengely ( számegyenes, koordinátaegyenes) Az Ox az az egyenes, amelyen az O pont ki van választva origó (koordináták eredete)(1. ábra), irány

O → x

néven szerepel pozitív irányés egy szakaszt jelölünk ki, amelynek hosszát vesszük hossz egysége.

2. definíció. Azt a szakaszt, amelynek hosszát hosszegységnek vesszük, léptéknek nevezzük.

A számtengely minden pontjának van egy koordinátája, amely valós szám. Az O pont koordinátája nulla. Az Ox sugáron fekvő tetszőleges A pont koordinátája megegyezik az OA szakasz hosszával. A numerikus tengely egy tetszőleges A pontjának a koordinátája, amely nem az Ox sugáron fekszik, negatív, és abszolút értékben megegyezik az OA szakasz hosszával.

3. definíció. Derékszögű derékszögű Oxy koordinátarendszer a síkon hívj fel kettőt kölcsönösen merőleges Ox és Oy numerikus tengelyekkel ugyanaz a skálaÉs közös referenciapont az O pontban, és úgy, hogy az Ox sugártól 90°-os szögben az Oy sugárig a forgás iránya óramutató járásával ellentétes irányban(2. ábra).

Jegyzet. A 2. ábrán látható Oxy derékszögű derékszögű koordinátarendszert nevezzük jobb koordinátarendszer, Nem úgy mint bal oldali koordinátarendszerek, amelyben az Ox gerenda Oy gerendához képest 90°-os forgatását az óramutató járásával megegyező irányban hajtjuk végre. Ebben az útmutatóban mi csak jobbkezes koordinátarendszereket vesszük figyelembe, anélkül, hogy konkrétan meghatározná.

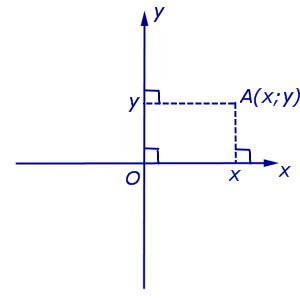
Ha bevezetünk valamilyen derékszögű Oxy koordinátarendszert a síkon, akkor a sík minden pontja megkapja két koordináta – abszcisszaÉs ordináta, amelyek kiszámítása a következőképpen történik. Legyen A tetszőleges pont a síkon. Vessünk merőlegeseket az A pontból A.A. 1 és A.A. 2. ábra az Ox és Oy egyenes vonalakhoz (3. ábra).

4. definíció. Az A pont abszcisszán a pont koordinátája A 1 az Ox számtengelyen az A pont ordinátája a pont koordinátája A 2 számtengelyen Oy.

Kijelölés A pont koordinátái (abszcissza és ordináta). A derékszögű derékszögű Oxy koordinátarendszerben (4. ábra) általában A-t jelölünk. A(x;y) vagy A = (x; y).

Jegyzet. O pont, ún eredet, koordinátái vannak O(0 ; 0) .

5. definíció. Az Oxy derékszögű derékszögű koordinátarendszerben az Ox numerikus tengelyt abszcissza tengelynek, az Oy numerikus tengelyt ordinátatengelynek nevezzük (5. ábra).

6. definíció. Mindegyik derékszögű derékszögű koordinátarendszer 4 negyedre (negyedrészre) osztja a síkot, amelyek számozását az 5. ábra mutatja.

7. definíció. Azt a síkot, amelyen egy derékszögű derékszögű koordinátarendszer adott, nevezzük Koordináta sík.

Jegyzet. Az abszcissza tengelyt a koordinátasíkon az egyenlet határozza meg y= 0, az ordinátatengelyt a koordinátasíkon az egyenlet adja meg x = 0.

1. állítás. Két pont közötti távolság Koordináta sík

A 1 (x 1 ;y 1) És A 2 (x 2 ;y 2)

számított képlet szerint

Bizonyíték . Tekintsük a 6. ábrát.

|A 1 A 2 | 2 = = (x 2 -x 1) 2 + (y 2 -y 1) 2 .

(1)

Ennélfogva,

Q.E.D.

Kör egyenlete a koordinátasíkon

Tekintsünk az Oxy koordinátasíkon (7. ábra) egy R sugarú kört, amelynek középpontja a pontban van. A 0 (x 0 ;y 0) .

Utasítás

Írja le a matematikai műveleteket szöveges formában, és írja be azokat a Google webhely főoldalának keresőmezőjébe, ha nem tud számológépet használni, de rendelkezik internet-hozzáféréssel. Ez a kereső egy beépített többfunkciós számológéppel rendelkezik, amely sokkal könnyebben használható, mint bármelyik másik. Nincs gombos felület – minden adatot szöveges formában, egyetlen mezőben kell megadni. Például ha ismert koordináták szélsőséges pontok szegmensben háromdimenziós A(51,34 17,2 13,02) és A(-11,82 7,46 33,5) koordinátarendszerben, akkor koordináták középpont szegmensben C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Ha a keresőmezőbe beírja az (51.34-11.82)/2, majd a (17.2+7.46)/2 és (13.02+33.5)/2 számokat, akkor a Google segítségével lekérheti koordináták C(19,76 12,33 23,26).

A kör szabványos egyenlete lehetővé teszi, hogy számos fontos információt megtudjon erről az ábráról, például a középpont koordinátáit, a sugár hosszát. Egyes feladatokban éppen ellenkezőleg, egy egyenletet kell létrehoznia adott paraméterek használatával.

Utasítás

Határozza meg, milyen információi vannak a körről a kapott feladat alapján. Ne feledje, hogy a végső cél a középpont koordinátáinak, valamint az átmérőnek a meghatározása. Minden tevékenységének ennek a konkrét eredménynek az elérésére kell irányulnia.

Használja a koordinátavonalakkal vagy más vonalakkal való metszéspontok jelenlétére vonatkozó adatokat. Vegye figyelembe, hogy ha a kör áthalad az abszcissza tengelyen, akkor a második koordinátája 0 lesz, ha pedig az ordinátatengelyen, akkor az elsőé. Ezek a koordináták lehetővé teszik, hogy megtalálja a kör középpontjának koordinátáit, és kiszámítsa a sugarat is.

Ne feledkezzünk meg a szekánsok és érintők alapvető tulajdonságairól. Különösen az a leghasznosabb tétel, hogy az érintkezési pontban a sugár és az érintő derékszöget alkot. De kérjük, vegye figyelembe, hogy előfordulhat, hogy bizonyítania kell a kurzus során használt összes tételt.

Oldja meg a legszokványosabb típusokat, hogy megtanulja azonnal látni, hogyan kell bizonyos adatokat használni a kör egyenletéhez. Tehát a már említett, közvetlenül megadott koordinátákkal és azokon a problémákon kívül, amelyekben a metszéspontok jelenlétéről adnak információt, a kör egyenletének összeállításához felhasználhatja a kör középpontjával, a kör hosszával kapcsolatos ismereteket. akkord, és amelyen ez az akkord fekszik.

A megoldáshoz készítsünk egy egyenlő szárú háromszöget, melynek alapja az adott húr lesz, az egyenlő oldalai pedig a sugarak. Összeállítás, amelyből könnyen megtalálhatja a szükséges adatokat. Ehhez elegendő egy síkban lévő szakasz hosszának meghatározására szolgáló képletet használni.

Videó a témáról

A kör alatt olyan alakzatot értünk, amely a középpontjától egyenlő távolságra lévő síkon sok pontból áll. Távolság a központtól a pontokig kör sugárnak nevezzük.

Poláris koordináták

A számot hívják poláris sugár pontok ill első poláris koordináta. A távolság nem lehet negatív, így bármely pont poláris sugara . Az első poláris koordinátát szintén görög betű („rho”) jelöli, de én a latin változathoz szoktam, és a jövőben is ezt fogom használni.

A számot hívják polárszög adott pont ill második poláris koordináta. A poláris szög jellemzően belül változik (ún főszögértékek). A tartomány használata azonban teljesen elfogadható, és bizonyos esetekben közvetlen szükség van az összes szögérték figyelembevételére a nullától a „plusz végtelenig”. Egyébként azt javaslom, hogy szokja meg a szög radián mértékét, mivel a fokokkal való operáció a felsőbb matematikában nem számít comme il fautnak.

A házaspárt úgy hívják poláris koordináták pontok Konkrét jelentésüket könnyű megtalálni. Egy derékszögű háromszög hegyesszögének érintője a szemközti oldal és a szomszédos oldal aránya: tehát maga a szög: . A Pitagorasz-tétel szerint a hipotenusz négyzete egyenlő a lábak négyzeteinek összegével: , ami a poláris sugarat jelenti:

És így, .

Egy pingvin jó, de egy nyáj jobb:


Negatív irányú sarkok Nyilakkal jelöltem, hátha az olvasók egy része még nem tudott erről a tájolásról. Igény szerint mindegyikhez „csavarhat” 1 fordulatot (rad. vagy 360 fok), és mellesleg kényelmes lesz táblázat értékeit:

De ezeknek a "hagyományosan" orientált szögeknek az a hátránya, hogy túl messzire (több mint 180 fokkal) az óramutató járásával ellentétes irányban vannak "csavarva". Előre vetem a kérdést: „miért van hátrány, és egyáltalán miért van szükség néhány negatív szögre?” A matematikában a legrövidebb és legracionálisabb utakat értékelik. Nos, a fizika szempontjából a forgásiránynak sokszor alapvető jelentősége van - mindannyian a kilincset rossz irányba húzva próbáltuk kinyitni az ajtót =)

A polárkoordinátákban történő pontalkotás rendje és technikája

A szép képek szépek, de poláris koordináta-rendszerben megszerkeszteni őket meglehetősen fáradságos feladat. Nincsenek nehézségek azokkal a pontokkal, amelyeknek poláris szögei vannak , példánkban ezek pontok ; A 45 fok többszörösei értékek sem okoznak nagy gondot: . De hogyan lehet helyesen és hozzáértően felépíteni mondjuk egy pontot?

Szükséged lesz egy kockás papírra, egy ceruzára és a következő rajzeszközökre: vonalzó, iránytű, szögmérő. Végső megoldásként meg lehet boldogulni egyetlen vonalzóval, vagy akár... anélkül is! Olvass tovább, és kapsz egy újabb bizonyítékot arra, hogy ez az ország legyőzhetetlen =)

1. példa

Szerkesszünk pontot a polárkoordináta-rendszerben.

Először is meg kell találnia a szög mértékét. Ha a sarok ismeretlen, vagy kétségei vannak, akkor mindig jobb használni asztal vagy egy általános képlet a radiánok fokokká alakítására. Tehát a szögünk (vagy).

Rajzoljunk poláris koordináta-rendszert (lásd a lecke elejét), és vegyünk fel egy szögmérőt. A kerek hangszer tulajdonosainak nem okoz nehézséget a 240 fokos jelölés, de valószínűleg a készülék félkör alakú változata lesz a kezében. A szögmérő teljes hiányának problémája nyomtató és olló jelenlétében kézimunkával oldják meg.

Két módja van: fordítsa meg a lapot és jelölje meg 120 fokkal, vagy „csavarja” fél fordulatot, és nézze meg az ellenkező szöget. Válasszuk a felnőtt módszert, és jelöljünk 60 fokot:


Vagy liliputi szögmérő, vagy óriási ketrec =) A szög méréséhez azonban a skála nem fontos.

Ceruzával rajzoljon egy vékony egyenes vonalat, amely áthalad a rúdon és a jelen:


Kiválasztottuk a szöget, most a sarki sugár következik. Vegyünk egy iránytűt és a vonal mentén megoldását 3 egységre állítottuk, leggyakrabban ez természetesen centiméter:

Most óvatosan ráhelyezzük a tűt a rúdra, és egy forgó mozdulattal kis bevágást készítünk (piros színű). A szükséges pont létrejött:


Iránytű nélkül is megteheti, ha a vonalzót közvetlenül a megépített egyenesre helyezi, és 3 centimétert mér. De mint később látni fogjuk, polárkoordináta-rendszerben történő konstrukcióval kapcsolatos problémákban Tipikus helyzet az, amikor két vagy több pontot kell azonos poláris sugárral megjelölni, így hatékonyabb a fém edzése. A rajzunkon különösen az iránytű lábának 180 fokkal elforgatásával könnyű egy második bevágást készíteni, és a pólushoz képest szimmetrikus pontot alkotni. Használjuk a következő bekezdés anyagának feldolgozásához:

Négyszögletes és poláris koordináta-rendszerek kapcsolata

Magától értetődően tegyük hozzá a poláris koordináta-rendszerhez egy „szabályos” koordináta-rácsot, és rajzoljon egy pontot a rajzon:

Ezt az összefüggést mindig célszerű szem előtt tartani, amikor polárkoordinátákat rajzolunk. Bár akarva-akaratlanul is minden további utalás nélkül sugallja magát.

Határozzuk meg a poláris és a derékszögű koordináták közötti kapcsolatot egy adott pont példáján. Tekintsünk egy derékszögű háromszöget, amelyben a hipotenusz egyenlő a poláris sugárral: , és a lábak egyenlőek a pont „X” és „Y” koordinátáival a derékszögű koordinátarendszerben: .

A hegyesszög szinusza a szemközti oldal és a hipotenusz aránya:

A hegyesszög koszinusza a szomszédos láb és a hipotenusz aránya:

Ugyanakkor megismételtük a szinusz, koszinusz (és kicsit korábbi érintő) definícióit egy általános iskola 9. osztályos tantervéből.

Kérjük, adjon hozzá olyan munkaképleteket a referenciakönyvéhez, amelyek egy pont derékszögű koordinátáit a poláris koordinátákon keresztül fejezik ki - többször is foglalkoznunk kell velük, és legközelebb most =)

Keressük meg egy pont koordinátáit egy téglalap alakú koordinátarendszerben:

És így:

Az így kapott képletek újabb kiskaput nyitnak a konstrukciós feladatban, amikor egyáltalán nem lehet szögmérőt nélkülözni: először megkeressük a pont derékszögű koordinátáit (természetesen a vázlatban), majd gondolatban megtaláljuk a kívánt helyet a rajzon és jelölje meg ezt a pontot. Az utolsó szakaszban egy vékony egyenes vonalat húzunk, amely áthalad a megszerkesztett ponton és a póluson. Ennek eredményeként kiderül, hogy a szöget állítólag szögmérővel mérték.

Vicces, hogy a nagyon kétségbeesett tanulók még vonalzó nélkül is megbirkóznak, helyette egy tankönyv, füzet vagy évfolyamkönyv sima szélét használják – elvégre a füzetgyártók ügyeltek a mérőszámokra, 1 négyzet = 5 milliméter.

Erről eszembe jutott egy jól ismert vicc, amelyben leleményes pilóták terveztek egy pályát egy falka Belomor mentén =) Bár a viccet félretéve, a vicc nem áll olyan messze a valóságtól, emlékszem, hogy az egyik belföldi járaton az orosz Föderáció, az összes navigációs műszer meghibásodott a repülőgépben, és a személyzet sikeresen leszállt a géppel egy szabályos pohár vízzel, amely megmutatta a gép talajhoz viszonyított szögét. És a leszállópálya – itt van, látszik a szélvédőről.

A lecke elején idézett Pitagorasz-tétel segítségével könnyen megkaphatjuk az inverz képleteket: , ezért:

Magát a „phi” szöget szabványosan az arctangenssel fejezik ki - teljesen ugyanaz, mint komplex szám argumentum minden bajával együtt.

A tápszerek második csoportját is célszerű referencia poggyászában elhelyezni.

Az egyes pontokat tartalmazó részletes kiigazítás után térjünk át a téma természetes folytatására:

Poláris koordinátákban lévő egyenes egyenlete

Lényegében az egyenlet egy poláris koordináta-rendszerben az a poláris sugár függvénye a poláris szögből (érv). Ebben az esetben a polárszöget veszik figyelembe radiánban(!) És folyamatosanértékeket vesz fel -tól (néha a végtelenségig kell tekinteni, vagy számos probléma esetén a kényelem érdekében től-ig). A „phi” szög minden értéke, amely benne van tartomány függvény, a poláris sugár egyetlen értékének felel meg.

A poláris funkció egyfajta radarhoz hasonlítható - amikor egy pólusból kiáramló fénysugár az óramutató járásával ellentétes irányba forog, és „észleli” (megrajzolja) a vonalat.

A poláris görbe szabványos példája az Arkhimédeszi spirál. A következő képen ő látható első kör– amikor a poláris szöget követő poláris sugár értéke 0-tól:

Ezen túlmenően, a sarki tengelyt a pontban keresztezve, a spirál tovább kitekerődik, végtelenül távol kerülve a pólustól. De az ilyen esetek meglehetősen ritkák a gyakorlatban; tipikusabb helyzet az, amikor minden további fordulatnál „ugyanazon a vonalon járunk”, amit a tartományban kaptunk.

Az első példában találkozunk a fogalommal definíciós tartomány polárfüggvény: mivel a poláris sugár nem negatív, a negatív szögek itt nem vehetők figyelembe.

! jegyzet : bizonyos esetekben szokás használni általánosított poláris koordináták, ahol a sugár negatív is lehet, és ezt a megközelítést egy kicsit később röviden tanulmányozzuk

Az Arkhimédész-spirálon kívül sok más híres görbe is van, de ahogy mondani szokás, a művészettel nem lehet betelni, ezért olyan példákat válogattam össze, amelyek nagyon gyakran megtalálhatók a valós gyakorlati feladatokban.

Először is a legegyszerűbb egyenletek és legegyszerűbb sorok:

A forma egyenlete megadja a pólusból kiinduló egyenletet Sugár. Valóban, gondolj bele, ha a szögérték Mindig(bármi legyen is az „er”) folyamatosan, akkor melyik vonalról van szó?

jegyzet : az általánosított poláris koordináta-rendszerben ez az egyenlet a póluson átmenő egyenest határoz meg

A forma egyenlete határozza meg... először tippeld meg - ha bárkinek A "phi" szög sugara állandó marad? Valójában ez a meghatározás kör középpontja a sugár pólusa .

Például, . Az érthetőség kedvéért keressük meg ennek az egyenesnek az egyenletét egy téglalap alakú koordinátarendszerben. Az előző bekezdésben kapott képlet segítségével végrehajtjuk a cserét:

Négyzetesítsük mindkét oldalt:

– kör egyenlete középponttal a 2. sugár origójában, amit ellenőrizni kellett.

A cikk létrehozása és megjelenése óta a vektorok lineáris függéséről és lineáris függetlenségéről Több levelet is kaptam az oldal látogatóitól, akik a következő szellemben tettek fel kérdést: "van egy egyszerű és kényelmes derékszögű koordinátarendszer, miért van szükség még egy ferde affin esetre?" A válasz egyszerű: a matematika arra törekszik, hogy mindent és mindenkit magába foglaljon! Ezenkívül adott helyzetben a kényelem is fontos - amint látja, az egyenlet rendkívüli egyszerűsége miatt sokkal kifizetődőbb polárkoordinátákban körrel dolgozni.

És néha egy matematikai modell előrevetíti a tudományos felfedezéseket. Tehát egy időben a Kazany Egyetem rektora N.I. Lobacsevszkij szigorúan bebizonyosodott, a sík tetszőleges pontján keresztül rajzolhatunk végtelen sok egyenes, ezzel párhuzamosan. Ennek eredményeként az egész tudományos világ megrágalmazta, de... ezt a tényt senki sem tudta megcáfolni. Csak egy jó évszázaddal később a csillagászok felfedezték, hogy a fény az űrben ívelt pályákon halad, ahol Lobacsevszkij nem-euklideszi geometriája, amelyet formálisan már jóval a felfedezés előtt dolgozott ki, működni kezd. Feltételezzük, hogy ez magának a térnek egy olyan tulajdonsága, amelynek görbülete a kis (csillagászati ​​mércével mért) távolságok miatt számunkra láthatatlan.

Nézzünk értelmesebb építési feladatokat:

2. példa

Építs egy vonalat

Megoldás: Először is keressük meg tartomány. Mivel a poláris sugár nem negatív, az egyenlőtlenségnek fennállnia kell. Emlékezhetsz a trigonometrikus egyenlőtlenségek megoldásának iskolai szabályaira, de az ehhez hasonló egyszerű esetekben javaslok egy gyorsabb és vizuálisabb megoldási módot:

Képzeljünk el egy koszinusz gráfot. Ha még nem regisztrált a memóriájában, akkor keresse meg az oldalon Elemi függvények grafikonjai. Mit mond nekünk az egyenlőtlenség? Azt mondja nekünk, hogy a koszinusz gráfot el kell helyezni nem kevesebb abszcissza tengely. És ez történik a szegmensben. És ennek megfelelően az intervallum nem megfelelő.

Így függvényünk definíciós tartománya: , vagyis a gráf a pólustól jobbra (a derékszögű rendszer terminológiájában - a jobb oldali félsíkban) helyezkedik el.

A poláris koordinátákban gyakran van egy homályos elképzelés arról, hogy melyik egyenes határoz meg egy adott egyenletet, ezért annak megalkotásához meg kell találni a hozzá tartozó pontokat – és minél többet, annál jobb. Általában egy-két tucatra (vagy még kevesebbre) korlátozódnak. A legegyszerűbb természetesen az, ha elvállalod táblázat szögértékei. A nagyobb érthetőség kedvéért egy fordulatot "csavarok" a negatív értékekre:

A koszinusz paritása miatt a megfelelő pozitív értékeket nem kell újra megszámolni:

Ábrázoljunk egy poláris koordináta-rendszert és ábrázoljuk a talált pontokat, miközben kényelmes egyszerre ugyanazokat az „er” értékeket ábrázolni, páros bevágásokat készítve egy iránytűvel a fent tárgyalt technológia segítségével:

A vonal elvileg jól megrajzolt, de a találgatás teljes igazolása érdekében keressük meg az egyenletét a derékszögű koordinátarendszerben. Alkalmazhatja a nemrég levezetett képleteket , de mesélek egy ravaszabb trükkről. Az egyenlet mindkét oldalát mesterségesen megszorozzuk „er”-vel: és kompaktabb átmeneti képleteket használunk:

Egy teljes négyzet kiválasztásával az egyenes egyenletét felismerhető formára hozzuk:

– kör egyenlete pontban középponttal, sugár 2.

Mivel a feltétel szerint egyszerűen el kellett végezni az építkezést, és ennyi, a talált pontokat simán összekötjük egy vonallal:

Kész. Nem baj, ha kicsit egyenetlen lesz, nem kellett tudni, hogy kör volt ;-)

Miért nem vettük figyelembe az intervallumon kívüli szögértékeket? A válasz egyszerű: nincs értelme. A függvény periodicitásából adódóan a megszerkesztett kör végtelen futása előtt állunk.

Könnyű elvégezni egy egyszerű elemzést, és arra a következtetésre jutni, hogy egy alakú egyenlet egy olyan átmérőjű kört határoz meg, amelynek középpontja a pontban van. Képletesen szólva, minden ilyen kör „ül” a poláris tengelyen, és szükségszerűen áthalad a póluson. Ha azonban, akkor a vidám társaság balra költözik - a sarki tengely folytatása felé (gondold meg, miért).

Hasonló, önállóan megoldható feladat:

3. példa

Szerkesszen meg egy egyenest, és keresse meg az egyenletét egy téglalap alakú koordinátarendszerben.

Rendszerezzük a probléma megoldásának menetét:

Először is megtaláljuk a függvény definíciós tartományát szinuszos hogy azonnal megértsük, hol a szinusz nem negatív.

A második lépésben a pontok polárkoordinátáit a segítségével számítjuk ki táblázat szögértékei; Elemezze, hogy csökkenthető-e a számítások száma?

A harmadik lépésben ábrázoljuk a pontokat a polárkoordináta-rendszerben, és óvatosan összekötjük egy vonallal.

És végül megtaláljuk az egyenes egyenletét a derékszögű koordinátarendszerben.

A mintamegoldás a lecke végén található.

Részletezzük az általános algoritmust és a szerkesztési technikát polárkoordinátákban
és jelentősen felgyorsítja az előadás második részében, de előtte még egy közös vonallal ismerkedünk meg:

Sarki Rózsa

Így van, szirmú virágról beszélünk:

4. példa

Szerkesszen meg egyenletekkel megadott egyeneseket polárkoordinátában

A sarki rózsa felépítésének két módja van. Először kövessük a recézett sávot, feltételezve, hogy a poláris sugár nem lehet negatív:

Megoldás:

a) Keressük meg a függvény definíciós tartományát:

Ez a trigonometrikus egyenlőtlenség grafikusan is könnyen megoldható: a cikk anyagaiból Gráfok geometriai transzformációi Ismeretes, hogy ha egy függvény argumentumát megduplázzuk, akkor a grafikonja 2-szeresére zsugorodik az ordináta tengelyére. Keresse meg a függvény grafikonját a lecke első példájában. Hol található ez a szinusz az x tengely felett? Időközönként . Következésképpen az egyenlőtlenséget a megfelelő szegmensek kielégítik, és tartomány funkciónk: .

Általánosságban elmondható, hogy a vizsgált egyenlőtlenségek megoldása végtelen számú szegmens uniója, de ismét csak egy periódusra vagyunk kíváncsiak.

Talán néhány olvasó könnyebben fogja használni az analitikus módszert a definíciós tartomány megtalálására. Vágjuk egyenlő részekreés mindenekelőtt keresse meg az első darab határait. A következőképpen érvelünk: a szinusz nem negatív, Amikor érvelését 0-tól rad-ig terjed. inkluzív. Példánkban: . A kettős egyenlőtlenség minden részét elosztva 2-vel, megkapjuk a szükséges intervallumot:

Most elkezdjük egymás után „90 fokos egyenlő darabokat vágni” az óramutató járásával ellentétes irányban:

– a talált szegmens természetesen beletartozik a definíciós tartományba;

– következő intervallum – nem tartalmazza;

– következő szegmens – tartalmazza;

– és végül az intervallum – nincs benne.

Akárcsak a százszorszép – „szeret, nem szeret, szeret, nem szeret” =) Azzal a különbséggel, hogy itt nincs jóslás. Igen, ez csak egyfajta szerelem kínai módon….

Így, a vonal pedig két egyforma szirmú rózsát ábrázol. Teljesen elfogadható a rajz sematikus megrajzolása, de nagyon tanácsos helyesen megtalálni és megjelölni szirmok teteje. A csúcsok megfelelnek definíciós tartomány szegmenseinek felezőpontjai, amelyeknek ebben a példában nyilvánvaló szögkoordinátái vannak . Ahol szirmok hossza vannak:

Íme a gondos kertész természetes eredménye:

Megjegyzendő, hogy a szirom hossza jól látható az egyenletből - mivel a szinusz korlátozott: , akkor az „er” maximális értéke biztosan nem haladja meg a kettőt.

b) Szerkesszük meg az egyenlet által adott egyenest! Nyilvánvaló, hogy ennek a rózsának a szirmának hossza is kettő, de mindenekelőtt a definíció tartománya érdekel. Alkalmazzuk az analitikus „szeletelés” módszert: a szinusz nem negatív, ha argumentuma a nullától a „pi”-ig terjedő tartományban van, ebben az esetben: . Az egyenlőtlenség minden részét elosztjuk 3-mal, és megkapjuk az első intervallumot:

Ezután elkezdjük „a pite darabokra vágását” rad által. (60 fok):
– a szegmens belép a definíciós tartományba;
– intervallum – nem szerepel;
– szegmens – elfér;
– intervallum – nem szerepel;
– szegmens – elfér;
– intervallum – nem szerepel.

A folyamat 360 fokban sikeresen befejeződött.

Így a meghatározás terjedelme a következő: .

Az egészben vagy részben végrehajtott cselekvések mentálisan könnyen végrehajthatók.

Építkezés. Ha az előző bekezdésben derékszögekkel és 45 fokos szögekkel minden jól működött, akkor itt egy kicsit trükköznie kell. Keressük szirmok teteje. A hosszuk már a feladat elején látható volt, csak a szögkoordinátákat kell kiszámítani, amelyek megegyeznek a definíciós tartomány szakaszainak felezőpontjaival:

Kérjük, vegye figyelembe, hogy a szirmok teteje között egyenlő távolságnak kell lennie, ebben az esetben 120 fok.

Célszerű a rajzot 60 fokos (zöld vonalakkal határolt) szektorokba jelölni, és megrajzolni a szirmok tetejének irányát (szürke vonalak). Kényelmes magát a csúcsokat megjelölni egy iránytű segítségével - mérjen meg egyszer 2 egység távolságot, és készítsen három bevágást a rajzolt 30, 150 és 270 fokos irányokban:

Kész. Megértem, hogy ez egy kellemetlen feladat, de ha mindent bölcsen akarsz elintézni, akkor időt kell töltened.

Fogalmazzunk meg egy általános képletet: alakú egyenlet, természetes szám), egy sarki szirmú rózsát definiál, amelynek szirmának hossza egyenlő .

Például az egyenlet egy 5 egység szirmhosszúságú négylevelű rózsát ad meg, az egyenlet egy 5 szirmú rózsát 3 egység szirmhosszúsággal. stb.

Előző cikk: Mekkora a fénysebesség Következő cikk: Harmonikus rezgések Az oszcillációs frekvencia fizikai képlete