Egy függvény szélső pontjai. Mik a függvény szélsőértékei: maximum és minimum kritikus pontjai

Ezeket az egyenlőtlenségeket átengedjük a Δ-nél lévő határértékre x→ 0 és figyelembe véve, hogy a derivált f "(x 0) létezik, ezért a bal oldali határérték nem függ attól, hogyan Δ x→ 0, kapjuk: Δ-nél x → 0 – 0 f"(x 0) ≥ 0 a Δ-nél x → 0 + 0 f"(x 0) ≤ 0. Mivel f"(x 0) definiál egy számot, akkor ez a két egyenlőtlenség csak akkor kompatibilis, ha f"(x 0) = 0.

A bizonyított tétel kimondja, hogy a maximum és a minimum pont csak az argumentum azon értékei között található, amelyeknél a derivált nullává válik.

Azt az esetet vizsgáltuk, amikor egy függvénynek egy adott szegmens minden pontján deriváltja van. Mi a helyzet azokban az esetekben, amikor a derivatíva nem létezik? Nézzünk példákat.

Példák.

1. y=|x|.

   A függvénynek nincs deriváltja a ponton x=0 (ezen a ponton a függvény grafikonjának nincs definiált érintője), de ezen a ponton a függvénynek van minimuma, mivel y(0)=0, és mindenre x≠ 0y > 0.



A függvénynek nincs at deriváltja x=0, mivel pontnál a végtelenbe megy x=0. De ezen a ponton a függvénynek van maximuma.



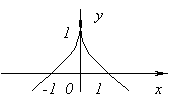
A függvénynek nincs at deriváltja x=0, mivel nál nél x→0. Ezen a ponton a függvénynek nincs sem maximuma, sem minimuma. Igazán, f(x)=0 és at x<0f(x)<0, а при x>0f(x)>0.



A megadott példákból és a megfogalmazott tételből tehát világos, hogy egy függvénynek csak két esetben lehet szélsőértéke: 1) azokon a pontokon, ahol a derivált létezik és egyenlő nullával; 2) azon a ponton, ahol a származék nem létezik.

Ha azonban valamikor x 0 ezt tudjuk f "(x 0 ) =0, akkor ebből nem lehet arra következtetni, hogy azon a ponton x 0 a függvénynek szélsőértéke van.

Például. .



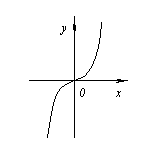
De időszak x A =0 nem szélsőséges pont, mivel ettől a ponttól balra a függvényértékek a tengely alatt találhatók Ökör, és jobbra fent.

Egy függvény tartományából származó argumentum értékeit, ahol a függvény deriváltja eltűnik vagy nem létezik, nevezzük. kritikus pontok.




A fentiekből következik, hogy a függvény szélsőpontjai a kritikus pontok közé tartoznak, de nem minden kritikus pont szélsőpont. Ezért egy függvény szélsőértékének megtalálásához meg kell találni a függvény összes kritikus pontját, majd ezeket a pontokat külön-külön meg kell vizsgálni a maximum és a minimum szempontjából. Ezt a célt szolgálja a következő tétel.

2. Tétel (Elegendő feltétel a szélsőség létezéséhez.) Legyen a függvény folytonos a kritikus pontot tartalmazó intervallumon x 0, és ennek az intervallumnak minden pontján differenciálható (kivéve talán magát a pontot x 0). Ha ezen a ponton balról jobbra haladva a derivált előjelet vált pluszról mínuszra, akkor a pontban x = x A 0 függvénynek maximuma van. Ha áthaladáskor x 0 balról jobbra, a derivált mínuszról pluszra változtatja az előjelet, ekkor a függvénynek ezen a ponton van minimuma.

Így ha

Bizonyíték. Először tegyük fel, hogy amikor áthaladunk x 0 a derivált az előjelet pluszról mínuszra változtatja, azaz. mindenki előtt x, közel a lényeghez x 0 f "(x)> 0 érte x< x 0 , f "(x)< 0 érte x> x 0 . Alkalmazzuk Lagrange tételét a különbségre f(x) - f(x 0 ) = f "(c)(x-x 0), hol c között fekszik xÉs x 0 .

1. Hadd x< x 0 . Akkor c< x 0 és f "c)> 0. Ezért f "(c)(x-x 0)< 0 és ezért

   f(x) - f(x 0 )< 0, azaz f(x)< f(x 0 ).

2. Hadd x > x 0 . Akkor c>x 0 és f "(c)< 0. Eszközök f "(c)(x-x 0)< 0. Ezért f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Így minden értékre x elég közel ahhoz x 0 f(x)< f(x 0 ) . Ez pedig azt jelenti, hogy pont x A 0 függvénynek maximuma van.

A minimumtétel második részét hasonló módon bizonyítjuk.



Illusztráljuk ennek a tételnek a jelentését az ábrán. Hadd f "(x 1 ) =0 és bármely x, elég közel ahhoz x 1, az egyenlőtlenségek teljesülnek

f "(x)< 0 órakor x< x 1 , f "(x)> 0 órakor x> x 1 .

Majd a pont bal oldalán x 1 a függvény a jobb oldalon növekszik és csökken, tehát amikor x = x 1 függvény növekvőről csökkenőre megy, vagyis van maximuma.

Hasonlóképpen figyelembe vehetjük a pontokat x 2 és x 3 .


A fentiek mindegyike sematikusan ábrázolható a képen:

Szabály az y=f(x) függvény tanulmányozására szélsőségre

1. Keresse meg egy függvény tartományát f(x).
2. Keresse meg egy függvény első deriváltját f "(x).
3. Határozza meg ehhez a kritikus pontokat:
   1. megtalálni az egyenlet valódi gyökereit f "(x)=0;
   2. megtalálja az összes értéket x amelyre a származék f "(x) nem létezik.
4. Határozzuk meg a kritikus ponttól balra és jobbra eső derivált előjelét! Mivel a derivált előjele két kritikus pont között állandó marad, elegendő a derivált előjelét a kritikus ponttól egy pontban balra és egy ponttal jobbra meghatározni.
5. Számítsa ki a függvény értékét a szélsőpontokban!

Példák. Fedezze fel a minimum és maximum funkciókat.




EGY SZEGMENS FUNKCIÓJÁNAK MAXIMÁLIS ÉS LEGKISEBB ÉRTÉKEI

A legnagyobb egy függvény értéke egy intervallumon a legnagyobb az ezen az intervallumon lévő összes értéke közül, és a legkisebb– értékei közül a legkisebb.

Vegye figyelembe a funkciót y=f(x) folyamatos a szakaszon [ a, b]. Mint ismeretes, egy ilyen függvény akár a szakasz határán, akár azon belül éri el maximális és minimális értékét. Ha egy függvény legnagyobb vagy legkisebb értékét a szakasz egy belső pontjában érjük el, akkor ez az érték a függvény maximuma vagy minimuma, vagyis a kritikus pontokon érhető el.

Így a következőket kapjuk szabály egy függvény legnagyobb és legkisebb értékének megtalálására egy szegmensen[ a, b] :

1. Keresse meg a függvény összes kritikus pontját az intervallumban ( a, b), és számítsa ki a függvényértékeket ezeken a pontokon.
2. Számítsa ki a függvény értékeit a szegmens végén, amikor x = a, x = b.
3. Az összes kapott érték közül válassza ki a legnagyobbat és a legkisebbet.

Keresse meg az y=(7x^2-56x+56)e^x függvény legnagyobb értékét a [-3; 2].

Megoldás

Keressük meg az eredeti függvény deriváltját a szorzati derivált képlet segítségével y"=(7x^2-56x+56)"e^x\,+ (7x^2-56x+56)\left(e^x\jobb)"= (14x-56)e^x+(7x^2-56x+56)e^x= (7x^2-42x)e^x= 7x(x-6)e^x. Számítsuk ki a derivált nulláit: y"=0;

7x(x-6)e^x=0,

x_1=0, x_2=6.

Rendezzük el a derivált előjeleit, és határozzuk meg az eredeti függvény monotonitási intervallumait egy adott szakaszon.

Az ábrából jól látható, hogy a [-3; 0] az eredeti függvény növekszik, a szegmensen pedig csökken. Így a szegmens legnagyobb értéke [-3; 2] értékét x=0 esetén érjük el, és egyenlő ezzel y(0)= 7\cdot 0^2-56\cdot 0+56=56.

Válasz

Feltétel

Keresse meg az y=12x-12tg x-18 függvény legnagyobb értékét a szakaszon \bal.

Megoldás

y"= (12x)"-12(tg x)"-(18)"= 12-\frac(12)(\cos ^2x)= \frac(12\cos ^2x-12)(\cos ^2x)\leqslant0. Ez azt jelenti, hogy az eredeti függvény nem növekszik a vizsgált intervallumon, és a legnagyobb értéket az intervallum bal végén, azaz x=0-nál veszi fel. A legnagyobb érték az y(0)= 12\cdot 0-12 tg (0)-18= -18.

Válasz

Forrás: „Matematika. Felkészülés a 2017-es egységes államvizsgára. Profilszint." Szerk. F. F. Liszenko, S. Kulabukhova.

Feltétel

Határozzuk meg az y=(x+8)^2e^(x+52) függvény minimális pontját!

Megoldás

A függvény minimumpontját a derivált segítségével találjuk meg. Keressük meg egy adott függvény deriváltját a szorzat deriváltjának, az x^\alpha és e^x deriváltjának képleteivel:

y"(x)= \left((x+8)^2\right)"e^(x+52)+(x+8)^2\left(e^(x+52)\right)"= 2(x+8)e^(x+52)+(x+8)^2e^(x+52)= (x+8)e^(x+52)(2+x+8)= (x+8)(x+10)e^(x+52).

Rendezzük el a derivált előjeleit, és határozzuk meg az eredeti függvény monotonitási intervallumait. e^(x+52)>0 bármely x esetén. y"=0 at x=-8, x=-10.

Az ábrán látható, hogy az y=(x+8)^2e^(x+52) függvénynek egyetlen x=-8 minimumpontja van.

Válasz

Forrás: „Matematika. Felkészülés a 2017-es egységes államvizsgára. Profilszint." Szerk. F. F. Liszenko, S. Kulabukhova.

Feltétel

Keresse meg a függvény maximális pontját y=8x-\frac23x^\tfrac32-106.

Megoldás

ODZ: x \geqslant 0. Keressük meg az eredeti függvény deriváltját:

y"=8-\frac23\cdot\frac32x^\tfrac12=8-\sqrt x.

Számítsuk ki a derivált nulláit:

8-\sqrt x=0;

\sqrt x=8;

x=64.

Rendezzük el a derivált előjeleit, és határozzuk meg az eredeti függvény monotonitási intervallumait.

Az ábrán látható, hogy az x=64 pont az adott függvény egyetlen maximális pontja.

Válasz

Forrás: „Matematika. Felkészülés a 2017-es egységes államvizsgára. Profilszint." Szerk. F. F. Liszenko, S. Kulabukhova.

Feltétel

Keresse meg az y=5x^2-12x+2\ln x+37 függvény legkisebb értékét a szakaszon \left[\frac35; \frac75\right].

Megoldás

ODZ: x>0.

Keressük meg az eredeti függvény deriváltját:

y"(x)= 10x-12+\frac(2)(x)= \frac(10x^2-12x+2)(x).

Határozzuk meg a derivált nulláit: y"(x)=0;

\frac(10x^2-12x+2)(x)=0,

5x^2-6x+1=0,

x_(1,2)= \frac(3\pm\sqrt(3^2-5\cdot1))(5)= \frac(3\pm2)(5),

x_1=\frac15\notin\left[\frac35; \frac75\right],

x_2=1\in\left[\frac35; \frac75\right].

Rendezzük el a derivált előjeleit, és határozzuk meg az eredeti függvény monotonitási intervallumait a vizsgált intervallumon.

Az ábráról jól látható, hogy a szegmensen \left[\frac35; 1\jobbra] az eredeti függvény csökken, és a szegmensen \bal növeli. Így a legkisebb érték a szegmensen \left[\frac35; \frac75\right] x=1-nél érhető el, és egyenlő y(1)= 5\cdot 1^2-12\cdot 1+2 \ln 1+37= 30.

Válasz

Forrás: „Matematika. Felkészülés a 2017-es egységes államvizsgára. Profilszint." Szerk. F. F. Liszenko, S. Kulabukhova.

Feltétel

Keresse meg az y=(x+4)^2(x+1)+19 függvény legnagyobb értékét a [-5; -3].

Megoldás

Keressük meg az eredeti függvény deriváltját a szorzati derivált képlet segítségével.

Amint láthatja, egy függvény szélsőértékének ez a jele megköveteli, hogy a ponton legalább másodrendű derivált legyen.

Példa.

Keresse meg a függvény szélsőértékét.

Megoldás.

Kezdjük a definíció tartományával:

Különböztessük meg az eredeti függvényt:

x=1, vagyis ez egy lehetséges szélsőpont. Megkeressük a függvény második deriváltját, és kiszámítjuk az értékét x = 1:

Ezért a második elégséges feltétel egy szélsőséghez, x=1- maximum pont. Akkor - maximális funkció.

Grafikus illusztráció.

Válasz:

Egy függvény szélsőértékének harmadik elégséges feltétele.

Legyen a függvény y=f(x) ig származékai vannak n-edik sorrend a pont szomszédságában és deriváltai ig n+1-edik sorrend magán a ponton. Hadd legyen.

Példa.

Keresse meg a függvény szélsőpontjait! .

Megoldás.

Az eredeti függvény egy racionális teljes függvény, definíciós tartománya a valós számok teljes halmaza.

Tegyük különbséget a függvény között:

A derivált nullára megy at , ezért ezek a lehetséges szélsőpontok. Használjuk a harmadik elégséges feltételt egy szélsőséghez.

Megkeressük a második deriváltot, és kiszámítjuk az értékét a lehetséges szélsőség pontjain (a közbenső számításokat elhagyjuk):

Következésképpen ez a maximum pont (a szélsőség harmadik elégséges jelére van n=1és ).

A pontok természetének megismerése megtaláljuk a harmadik deriváltot, és kiszámítjuk az értékét a következő pontokban:

Ezért a függvény inflexiós pontja ( n=2és ).

A lényeggel kell foglalkozni. Megkeressük a negyedik deriváltot, és ezen a ponton kiszámítjuk az értékét:

Ezért a függvény minimumpontja.

Grafikus illusztráció.

Válasz:

A maximum pont a függvény minimumpontja.

10. Függvény szélsőértéke Extrémum definíciója

Az y = f(x) függvényt meghívjuk növekvő (csökkenő) egy bizonyos intervallumban, ha x 1-re< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x 2)).

Ha az y = f(x) differenciálható függvény növekszik (csökken) egy intervallumon, akkor a deriváltja ezen az intervallumon f " (x)  0

(f " (x)  0).

Pont x O hívott helyi maximum pont (minimális) f(x) függvény, ha van a pont szomszédsága x O, minden olyan pontra igaz, amelynek f(x) ≤ f(x о) (f(x) ≥ f(x о)) egyenlőtlenség igaz.

A maximum és minimum pontokat hívjuk szélsőséges pontok, és a függvény értékei ezeken a pontokon az ő szélsőségek.

Extrém pontok

Az extrémumhoz szükséges feltételek. Ha a lényeg x O az f(x) függvény szélsőpontja, akkor vagy f " (x o) = 0, vagy f (x o) nem létezik. Az ilyen pontokat ún. kritikai, maga a függvény pedig a kritikus pontban van definiálva. Egy függvény szélsőpontját a kritikus pontjai között kell keresni.

Az első elégséges feltétel. Hadd x O- kritikus pont. Ha f "(x) ponton való áthaladáskor x O módosítja a plusz jelet mínuszra, majd a pontra x O a függvénynek van maximuma, egyébként minimuma. Ha a kritikus ponton áthaladva a derivált nem vált előjelet, akkor a pontban x O nincs szélsőség.

Második elégséges feltétel. Legyen az f(x) függvénynek egy f " (x) deriváltja a pont közelében x O a második derivált pedig magában a pontban x O. Ha f "(x o) = 0, >0 (<0), то точка x O az f(x) függvény lokális minimum (maximum) pontja. Ha =0, ​​akkor vagy az első elégséges feltételt kell használnia, vagy magasabb származékokat kell használnia.

Egy szakaszon az y = f(x) függvény akár a kritikus pontokon, akár a szakasz végein elérheti minimális vagy maximum értékét.

3.22. példa. Határozzuk meg az f(x) = 2x 3 - 15x 2 + 36x - 14 függvény szélsőértékét.

Megoldás. Mivel f "(x) = 6x 2 - 30x +36 = 6(x ​​-2) (x - 3), akkor az x 1 = 2 és x 2 = 3 függvény kritikus pontjai. Extréma csak Ezek a pontok tehát az x 1 = 2 ponton áthaladva a derivált előjelét mínuszra változtatja, akkor az x 2 = 3 ponton áthaladva a derivált az előjelét mínuszra változtatja pluszhoz, ezért az x 2 = 3 pontban a függvénynek van egy minimuma Az x 1 = 2 és x 2 = 3 pontokban a függvény értékeit megkapjuk a függvény szélsőértékét: maximum f(. 2) = 14 és minimum f(3) = 13.

Mielőtt megtanulná, hogyan találja meg egy függvény szélsőértékét, meg kell értenie, mi az a szélsőség. Az extrémum legáltalánosabb definíciója az, hogy a matematikában használatos módon a függvény legkisebb vagy legnagyobb értéke egy számegyenes vagy gráf egy bizonyos halmazán. Azon a helyen, ahol a minimum található, megjelenik a minimum szélsőség, ahol pedig a maximum, ott a maximum szélsőség. Az olyan tudományágban is, mint a matematikai elemzés, egy függvény lokális szélsőségeit azonosítják. Most nézzük meg, hogyan találhatunk szélsőséges pontokat.

A matematikában az extrémek a függvények legfontosabb jellemzői közé tartoznak, ezek mutatják a legnagyobb és legkisebb értékeit. A szélsőségek főleg a megtalált funkciók kritikus pontjain találhatók. Érdemes megjegyezni, hogy a függvény a szélsőponton gyökeresen megváltoztatja az irányát. Ha kiszámítja a szélsőpont deriváltját, akkor a definíció szerint nullának kell lennie, vagy teljesen hiányzik. Így ahhoz, hogy megtudja, hogyan találja meg egy függvény szélsőértékét, két egymást követő feladatot kell végrehajtania:

• keresse meg a függvény deriváltját, amelyet a feladatnak meg kell határoznia;
• keresse meg az egyenlet gyökereit.

Az extrémum megtalálásának sorrendje

1. Írd fel a megadott f(x) függvényt. Keresse meg f "(x) elsőrendű deriváltját. Az eredményül kapott kifejezést nullával egyenlővé tesszük.
2. Most meg kell oldania a kapott egyenletet. A kapott megoldások az egyenlet gyökerei, valamint a meghatározandó függvény kritikus pontjai lesznek.
3. Most határozzuk meg, hogy mely kritikus pontok (maximum vagy minimum) vannak a talált gyökerek. A következő lépés, miután megtanultuk, hogyan kell megtalálni egy függvény szélsőpontjait, meg kell keresni a kívánt f "(x) függvény második deriváltját. A talált kritikus pontok értékeit be kell majd cserélni egy adott egyenlőtlenség, majd számítsa ki, mi történik.
4. Marad a kezdeti függvény értékének kiszámítása a függvény szükséges maximum- és minimumpontjain. Ehhez a kapott értékeket behelyettesítjük a függvénybe, és kiszámítjuk. Érdemes azonban megjegyezni, hogy ha a kritikus pont maximumnak bizonyul, akkor az extrémum maximum lesz, ha pedig minimum, akkor analógia szerint minimum.

Algoritmus a szélsőség megtalálásához

A megszerzett ismeretek összegzésére készítünk egy rövid algoritmust a szélsőséges pontok megtalálására.

1. Megtaláljuk egy adott függvény definíciós tartományát és intervallumait, amelyek pontosan meghatározzák, hogy a függvény mely intervallumokon folytonos.
2. Keresse meg az f "(x) függvény deriváltját.
3. Kiszámítjuk az y = f (x) egyenlet kritikus pontjait.
4. Elemezzük az f (x) függvény irányának változásait, valamint az f "(x) derivált előjelét, ahol a kritikus pontok felosztják a függvény definíciós tartományát.
5. Most határozzuk meg, hogy a grafikon minden pontja maximum vagy minimum.
6. A függvény értékeit azokon a pontokon találjuk, amelyek szélsőségesek.
7. A vizsgálat eredményét rögzítjük - a monotonitás szélsőségeit és intervallumait. Ez minden. Most megvizsgáltuk, hogyan találhat szélsőséget bármely intervallumon. Ha egy függvény bizonyos intervallumán kell extrémumot találni, akkor ez hasonló módon történik, csak az elvégzett kutatás határait kell figyelembe venni.

Tehát megvizsgáltuk, hogyan találjuk meg egy függvény szélsőpontját. Egyszerű számítások segítségével, valamint a deriváltak keresésének ismeretével bármely szélsőértéket megtalálhat és kiszámolhat, valamint grafikusan jelezheti. A szélsőségek megtalálása a matematika egyik legfontosabb része, mind az iskolában, mind a felsőoktatásban, ezért ha megtanulja helyesen azonosítani őket, akkor a tanulás sokkal könnyebbé és érdekesebbé válik.

Egy függvény természetének meghatározásához és viselkedéséről beszélni meg kell találni a növekedés és a csökkenés intervallumait. Ezt a folyamatot függvénykutatásnak és grafikusnak nevezik. A szélsőpontot egy függvény legnagyobb és legkisebb értékének megtalálásakor használjuk, mivel ezeknél a függvény az intervallumtól növekszik vagy csökken.

Ez a cikk feltárja a definíciókat, megfogalmazza az intervallum növekedésének és csökkenésének kellő jelét, valamint a szélsőség fennállásának feltételét. Ez vonatkozik a példák és problémák megoldására. A függvények differenciálásáról szóló részt meg kell ismételni, mert a megoldáshoz a derivált keresését kell használni.

Yandex.RTB R-A-339285-1 1. definíció

Az y = f (x) függvény növekszik az x intervallumon, ha bármely x 1 ∈ X és x 2 ∈ X, x 2 > x 1 esetén teljesül az f (x 2) > f (x 1) egyenlőtlenség. Más szavakkal, az argumentum nagyobb értéke a függvény nagyobb értékének felel meg.

2. definíció

Az y = f (x) függvényt csökkenőnek tekintjük az x intervallumon, ha bármely x 1 ∈ X, x 2 ∈ X, x 2 > x 1 esetén az f (x 2) > f (x 1) egyenlőség igaznak számít. Más szóval, egy nagyobb függvényérték kisebb argumentumértéknek felel meg. Tekintsük az alábbi ábrát.

Megjegyzés: Ha a függvény határozott és folytonos a növekedési és csökkenési intervallum végén, azaz (a; b), ahol x = a, x = b, akkor a pontok a növekedés és a csökkenés intervallumába kerülnek. Ez nem mond ellent a definíciónak, hanem azt jelenti, hogy az x intervallumon történik.

Az y = sin x típusú elemi függvények fő tulajdonságai az argumentumok valós értékeinek bizonyossága és folytonossága. Innen azt kapjuk, hogy a szinusz növekszik a - π 2 intervallum alatt; π 2, akkor a szegmens növekedésének alakja - π 2; π 2.

Az x 0 pontot nevezzük maximális pont az y = f (x) függvényre, amikor x minden értékére érvényes az f (x 0) ≥ f (x) egyenlőtlenség. Maximális funkció a függvény értéke egy pontban, és y m a x jelöli.

Az x 0 pontot az y = f (x) függvény minimális pontjának nevezzük, amikor x minden értékére érvényes az f (x 0) ≤ f (x) egyenlőtlenség. Minimális funkciók a függvény értéke egy pontban, és y m i n alakú jelölése van.

Az x 0 pont szomszédságait tekintjük extrém pontok,és a szélsőpontoknak megfelelő függvény értéke. Tekintsük az alábbi ábrát.

A függvény legnagyobb és legkisebb értékével rendelkező függvény szélsőértéke. Tekintsük az alábbi ábrát.

Az első ábra azt mondja, hogy meg kell találni a függvény legnagyobb értékét az [a; b ] . Maximum pontok felhasználásával található, és egyenlő a függvény maximális értékével, a második ábra pedig inkább az x = b-nél lévő maximális pont megtalálásához hasonlít.

Elegendő feltételek egy függvény növekedéséhez és csökkenéséhez

Egy függvény maximumának és minimumának meghatározásához szélsőségjeleket kell alkalmazni abban az esetben, ha a függvény teljesíti ezeket a feltételeket. Az első jelet tekintik a leggyakrabban használtnak.

Az első elégséges feltétel az extrémumhoz

Legyen adott egy y = f (x) függvény, amely az x 0 pont ε szomszédságában differenciálható, és az adott x 0 pontban folytonos. Innentől azt kapjuk

• ha f " (x) > 0 x ∈ (x 0 - ε ; x 0) és f " (x) esetén< 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
• amikor f "(x)< 0 с x ∈ (x 0 - ε ; x 0) и f " (x) >0 x ∈ (x 0 ; x 0 + ε) esetén, akkor x 0 a minimumpont.

Más szavakkal, megkapjuk a feltételeket a jel beállításához:

• ha a függvény folytonos az x 0 pontban, akkor van változó előjelű deriváltja, azaz +-ból - -be, ami azt jelenti, hogy a pontot maximumnak nevezzük;
• ha a függvény folytonos az x 0 pontban, akkor van egy deriváltja, melynek előjele -ról +-ra változik, ami azt jelenti, hogy a pontot minimumnak nevezzük.

Egy függvény maximális és minimális pontjának helyes meghatározásához kövesse a keresési algoritmust:

• keresse meg a definíciós tartományt;
• keresse meg a függvény deriváltját ezen a területen;
• azonosítsa a nullákat és pontokat, ahol a függvény nem létezik;
• a derivált előjelének meghatározása intervallumokon;
• válassza ki azokat a pontokat, ahol a függvény előjelet vált.

Tekintsük az algoritmust úgy, hogy több példát is megoldunk egy függvény szélsőértékének meghatározására.

1. példa

Határozzuk meg az adott y = 2 (x + 1) 2 x - 2 függvény maximális és minimum pontját!

Megoldás

Ennek a függvénynek a definíciós tartománya minden valós szám, kivéve x = 2. Először keressük meg a függvény deriváltját, és kapjuk meg:

y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2 ) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2

Innen látjuk, hogy a függvény nullái x = - 1, x = 5, x = 2, vagyis minden zárójelet nullával kell egyenlővé tenni. Jelöljük a számtengelyen, és kapjuk:

Most minden intervallumból meghatározzuk a derivált előjeleit. Ki kell választani egy, az intervallumban szereplő pontot, és be kell cserélni a kifejezésbe. Például az x = - 2, x = 0, x = 3, x = 6 pontok.

Ezt értjük

y" (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, ami azt jelenti, hogy a - ∞ - 1 intervallumnak van pozitív deriváltja.

y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0

Mivel a második intervallum nullánál kisebbnek bizonyult, ez azt jelenti, hogy az intervallum deriváltja negatív lesz. A harmadik mínuszos, a negyedik plusz. A folytonosság meghatározásához figyelni kell a derivált előjelére, ha az megváltozik, akkor ez egy szélsőpont.

Azt találjuk, hogy az x = - 1 pontban a függvény folytonos lesz, ami azt jelenti, hogy a derivált előjelet vált +-ról --ra. Az első jel szerint azt kapjuk, hogy x = - 1 egy maximumpont, ami azt jelenti, hogy megkapjuk

y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0

Az x = 5 pont azt jelzi, hogy a függvény folytonos, és a derivált előjelet vált –ról +-ra. Ez azt jelenti, hogy x = -1 a minimumpont, és a meghatározás alakja

y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24

Grafikus kép

Válasz: y m a x = y (- 1) = 0, y m i n = y (5) = 24.

Érdemes odafigyelni arra, hogy a szélsőérték első elégséges kritériumának alkalmazása nem igényli, hogy a függvény az x 0 pontban differenciálható legyen, ami leegyszerűsíti a számítást.

2. példa

Határozzuk meg az y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 függvény maximális és minimum pontját!

Megoldás.

Egy függvény tartománya minden valós szám. Ez egyenletrendszerként írható fel a következő formájú:

1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0

Ezután meg kell találnia a származékot:

y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0

Az x = 0 pontnak nincs deriváltja, mert az egyoldali határértékek eltérőek. Ezt kapjuk:

lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y "x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3

Ebből következik, hogy a függvény folytonos az x = 0 pontban, akkor számolunk

lim y x → 0 - 0 = határ x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8

Számításokat kell végezni az argumentum értékének meghatározásához, amikor a derivált nullává válik:

1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0

1 2 x 2 - 4 x + 22 3, x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0

Minden kapott pontot egyenes vonalon kell megjelölni az egyes intervallumok előjelének meghatározásához. Ezért minden intervallumra tetszőleges ponton kell kiszámítani a deriváltot. Például vehetünk x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6 értékű pontokat. Ezt értjük

y" (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y "(- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 (- 1) 2 - 4 (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 év "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0

Az egyenes vonalon lévő kép így néz ki

Ez azt jelenti, hogy arra a következtetésre jutunk, hogy a szélsőség első jeléhez kell folyamodni. Számoljuk ki és találjuk meg

x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , akkor innentől a maximális pontok x = - 4 + 2 3 3 , x = 4 - 2 3 3 értékek

Térjünk át a minimumok kiszámítására:

y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 év m i n = év 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3

Számítsuk ki a függvény maximumait. Ezt értjük

év m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 év m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3

Grafikus kép

Válasz:

é m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 év m i n = é 4 + 2 3 3 = - 8 27 3 év m a x = é - 4 + 2 3 3 = 3 m 2 = y 4 - 2 3 3 = 8 27 3

Ha adott egy f "(x 0) = 0 függvény, akkor ha f "" (x 0) > 0, akkor azt kapjuk, hogy x 0 minimumpont, ha f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .

3. példa

Határozzuk meg az y = 8 x x + 1 függvény maximumát és minimumát!

Megoldás

Először is megtaláljuk a definíció tartományát. Ezt értjük

D(y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0

Meg kell különböztetni a függvényt, ami után megkapjuk

y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x

Ha x = 1, a derivált nullává válik, ami azt jelenti, hogy a pont egy lehetséges szélsőérték. A tisztázás érdekében meg kell találni a második deriváltot, és ki kell számítani az értéket x = 1-nél. Kapunk:

y "" = 4 - x + 1 (x + 1) 2 x " = = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2 " x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) "x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0

Ez azt jelenti, hogy a 2 elégséges feltételt használva egy szélsőséghez azt kapjuk, hogy x = 1 a maximális pont. Ellenkező esetben a bejegyzés így néz ki: y m a x = y (1) = 8 1 1 + 1 = 4.

Grafikus kép

Válasz: y m a x = y (1) = 4 ..

Az y = f (x) függvény deriváltja n-edrendig egy adott x 0 pont ε szomszédságában, deriváltja pedig n + 1. rendig az x 0 pontban. Ekkor f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .

Ebből következik, hogy ha n páros szám, akkor x 0 inflexiós pontnak tekinthető, ha n páratlan szám, akkor x 0 extrémumpont, és f (n + 1) (x 0) > 0, akkor x 0 egy minimumpont, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.

4. példa

Határozzuk meg az y y = 1 16 (x + 1) 3 (x - 3) 4 függvény maximális és minimum pontját!

Megoldás

Az eredeti függvény egy racionális teljes függvény, ami azt jelenti, hogy a definíciós tartomány minden valós szám. Szükséges a funkció megkülönböztetése. Ezt értjük

y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)

Ez a derivált nullára megy, ha x 1 = - 1, x 2 = 5 7, x 3 = 3. Vagyis a pontok lehetnek lehetséges szélsőpontok. Az extrémumra a harmadik elégséges feltételt kell alkalmazni. A második derivált megtalálása lehetővé teszi egy függvény maximumának és minimumának pontos meghatározását. A második derivált a lehetséges szélsőértékének pontjain kerül kiszámításra. Ezt értjük

y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0

Ez azt jelenti, hogy x 2 = 5 7 a maximális pont. A 3. elégséges feltételt alkalmazva azt kapjuk, hogy n = 1 és f (n + 1) esetén 5 7< 0 .

Meg kell határozni az x 1 = - 1, x 3 = 3 pontok jellegét. Ehhez meg kell találnia a harmadik deriváltot, és ki kell számítania az értékeket ezeken a pontokon. Ezt értjük

y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0

Ez azt jelenti, hogy x 1 = - 1 a függvény inflexiós pontja, mivel n = 2 és f (n + 1) esetén (- 1) ≠ 0. Meg kell vizsgálni az x 3 = 3 pontot. Ehhez keressük meg a 4. deriváltot, és ezen a ponton végezzük el a számításokat:

y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0

A fentiek alapján azt a következtetést vonjuk le, hogy x 3 = 3 a függvény minimumpontja.

Grafikus kép

Válasz: x 2 = 5 7 az adott függvény maximumpontja, x 3 = 3 a minimumpontja.

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt