Kockás papírra 28-as területű kört rajzolunk

December 7-én tehát megtörtént a következő matematika tesztvizsga. A legutóbbi alkalomhoz hasonlóan 16 lehetőséget kínáltak a hallgatóknak – mindegyik a közeljövőben megjelenik a honlapon.

A vizsgáról általában a következők mondhatók el:

A vizsga továbbra is logaritmus nélküli (de derivált) és derivált nélküli (de logaritmusos) opciókra oszlik. Ennek az az oka, hogy az iskolákban párhuzamosan két program működik: az egyik szerint a 10. évfolyamon a származékokat, a 11. évfolyamon a logaritmusokat, a másik szerint fordítva. Arra azonban fel kell készülnünk, hogy már 2012. január-februárban minden változatban lesz logaritmus és derivált is;

Az új lehetőségek nagyon hasonlítottak egymáshoz, a problémák körülményei szinte azonosak - csak a számok és tulajdonképpen a válaszok különböznek. Ez egyrészt jó, hiszen minden diák megközelítőleg egyenlő körülmények között van. De másrészt ebben semmi jó, hiszen a valós lehetőségek jelentősen (nagyon jelentősen!) eltérnek majd egymástól;

Furcsa módon új problémák jelentek meg, amelyekre korábban egyáltalán nem gondoltak – bárhol és soha. Mindenekelőtt ez a valószínűségszámításra vonatkozik, amelyet az alábbiakban tárgyalok. Az ilyen „újítások” semmivé teszik az egységesítési lehetőségeken végzett munkát.

Következtetések: Az új képzési lehetőségekben nincs jelentős változás. Maguk a lehetőségek egyre jobban hasonlítottak egymáshoz, de némelyiküknek új feladatai vannak, amelyekkel a legtöbb diák biztosan nem tud megbirkózni.

Most pedig nézzünk konkrét problémákat, különösen a valószínűségszámítás „újoncainak”.

B1 probléma: mennyibe kerül egy liter benzin?

A matematika egységes államvizsga előírásai szerint a B1 gyakorlati tartalmú feladat. Esetünkben az ügyfél vesz benzint és kap aprópénzt. Meg kell találnia ennek a változásnak a méretét vagy a vásárolt benzin mennyiségét.

Egy ilyen probléma megoldásához fontos tudni egyetlen tényt – nevezzük ezt szorzás törvénye. Ha ismert egy liter benzin költsége p és a vásárolt literek száma n, akkor a teljes költség p · n lesz. Például, ha 1 liter ára 28 rubel, és 15 litert szeretnénk vásárolni, akkor 28 · 15 = 420 rubelt kell fizetnünk.

Ráadásul egyszer s mindenkorra meg kellene tanulnod, mi az a megadás. Gondolj bele: ha elmész egy kioszkba, és veszel egy üveg vodkát 350 rubelért, de csak 1000 rubel van a zsebedben, a pénztáros 1000 − 350 = 650 rubelt ad vissza. Ez a változás – a tényleges vételár és az Ön által fizetett összeg közötti különbség. A változást mindig pozitív számként fejezzük ki.

Feladat. Egy benzinkúton az ügyfél 1000 rubelt adott a pénztárosnak, és 22 liter benzinnel töltötte meg a tartályt 31 rubel áron. 80 kop. literenként Milyen aprópénzt kapjon az ügyfél a pénztárostól? Válaszát rubelben fejezze ki.

Először is fejezzük ki a benzin árát rubelben (kopecka nélkül): 31 rubel. 80 kop. - ez 31,8 rubel.

Tehát egy liter 31,8 rubelbe kerül. Akkor 22 liter ára 22 · 31,8 = 699,6 rubel. De az ügyfél 1000 rubelt adott a pénztárosnak, tehát 1000 − 699,6 = 300,4 rubelt kell kapnia. Ez a válasz – nem szükséges a számot kopejkára visszaváltani.

Feladat. Egy benzinkúton az ügyfél 1000 rubelt adott a pénztárosnak, és kérte, hogy töltsön fel benzint, amíg meg nem telik a tank. A benzin ára 30 rubel. 30 kopejkát literenként Az ügyfél 303 rubelt kapott aprópénzben. 10 kopejkát Hány liter benzint öntöttek a tartályba?

Váltsunk át minden árat rubelre: 30 rubel. 30 kopecka 30,3 rubel; 303 dörzsölje. 10 kopejkát - ez 303,1 rubel.

Most pedig nézzük a problémafelvetést. Ha az ügyfél 1000 rubelt adott a pénztárosnak, és 303,1 rubelt kapott cserébe, akkor a tényleges költségek (vételár) 1000 − 303,1 = 696,9 rubel.

Mivel 1 liter benzin ára 30,3 rubel, akkor 696,9 rubelért 696,9: 30,3 = 23 litert vásárolhat. Ez a válasz.

B3. feladat: pizzaszeletelés megtanulása. Sejt nélkül

Ahogy vártam, néhány probléma a B3-ban arra kért bennünket, hogy keressük meg egy sokszög területét, amelyet a csúcsok koordinátái adnak meg. Ebben az esetben a rajzban nem volt koordináta rács. Egyéb problémák a szektorok területeinek megtalálását igényelték.

A sokszögekkel kapcsolatos problémákat alapvetően meg lehet oldani - csak meg kell építeni a leírt téglalapot (lásd a „Sokszögek területei egy koordináta-rácson”). Azt is tudjuk, hogyan kell szektorokkal dolgozni (lásd „Kör területe”), de ezúttal a probléma írói kifinomultabb terveket javasoltak.

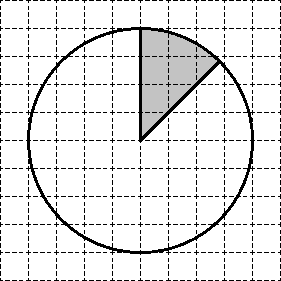
Feladat. Egy kockás papírra rajzolunk egy kört, amelynek területe 16. Keresse meg az árnyékolt ábra területét.

Vágjuk a kört 8 egyenlő részre, mint egy pizzát. Az egyes szektorok területe 16: 8 = 2 (lásd a rajzot).

Nyilvánvalóan az árnyékolt rész 6 ilyen szektorból áll, így a területe 6 2 = 12.

Feladat. Határozza meg annak a négyszögnek a területét, amelynek csúcsainak koordinátái (1; 1), (10; 1), (7; 9), (2; 9)

Nyilvánvaló, hogy ez egy trapéz, így kiszámíthatjuk a trapéz területére vonatkozó képlet segítségével. De követjük a hagyományos utat: megszerkesztjük a leírt téglalapot, és megjelöljük az összes vágás hosszát. A következő képet kapjuk:

Meg kell találni az S téglalap teljes területét, valamint az S 1 és S 2 háromszögek kivágandó területeit:
S=9,8=72;
S1=0,518=4;
S2=0,538=12;
S out = S − (S 1 + S 2) = 72 − (4 + 12) = 56.

B7. feladat: Trigonometria

Abszolút standard feladat trigonometrikus függvények kiszámításához és a koordinátakörrel való munkavégzéshez. A legtöbb hiba azokban a változatokban fordult elő, amelyekben érintőt vagy kotangenst kellett találni, mivel a többszintű törtek az ilyen problémák megoldásának legvégén keletkeznek.

Sajnos a legtöbb 11. osztályos tanuló még mindig nem tudja, hogyan kell többszintű törtekkel dolgozni. Ebben azonban csak a tanár a hibás. Meglepő módon a legtöbb iskolai matematikatanár maga nem tudja, hogyan kell kiszámítani az ilyen törteket (lásd a „Komplex kifejezések törtekkel. Eljárás” című leckét).

Személy szerint úgy gondolom, hogy ilyen embereket nem szabadna engedni, hogy iskolákban dolgozzanak. Azt a matematikatanárt, aki nem tud több emeletes törtekkel dolgozni, azonnal ki kell zárni, és bányákba kell küldeni uránt ásni.

Ha Önnek is gondjai vannak a többemeletes törtekkel, egyszerűen csak tanulmányozza a fenti leckét, majd töltse ki a kísérő teszteket. Higgye el, nincs semmi bonyolult ezekben a törtrészekben.

B10. feladat: Petya az érméivel

A valószínűségszámítással kapcsolatos problémák mindig is változatosak voltak, de ezúttal úgy tűnik, hogy a fordítók túlszárnyalták magukat. Például egyes lehetőségeknél a választ a legközelebbi századra kellett kerekíteni. Ellenkező esetben az eredmény egy végtelen tizedes tört volt. De a legtöbb diák csak egy számológép segítségével tudja megtalálni ezt a törtet, amelyet tilos használni a matematika egységes államvizsgáján.

De a kerekítés nem olyan rossz. Sokkal érdekesebbnek tűnnek az érmékkel kapcsolatos problémák, amelyek először a képzési verziókban jelentek meg. Az ilyen problémák megoldásához tudnia kell, hogy mik a binomiális együtthatók - és a közeljövőben mindenképpen megvizsgáljuk ezt a témát. Egyelőre két konkrét probléma elemzésére szorítkozunk az 1. és 4. lehetőség közül (logaritmus nélkül):

Feladat. Petya zsebében 4 rubel és 2 rubel volt. Petya anélkül, hogy ránézett volna, áttett egy másik zsebbe vagy három érmét. Határozza meg annak valószínűségét, hogy mindkét kétrubeles érme ugyanabban a zsebben van.

Mivel mindkét kétrubeles érme ugyanabba a zsebbe került, két lehetőség van: vagy Petya egyáltalán nem utalta át őket, vagy mindkettőt egyszerre.

Az első esetben, amikor a kétrubeles érméket nem tolták el, 3 rubel érméket kell eltolni. Mivel összesen 4 ilyen érme van, a módok száma megegyezik a 4-3 kombinációk számával: C 4 3.

A második esetben, amikor mindkét kétrubeles érmét átutalták, egy másik rubel érmét kell átadni. 4 meglévő közül kell kiválasztani, és ennek a módjai megegyeznek a 4-től 1-ig terjedő kombinációk számával: C 4 1.

Most nézzük meg az érmék átrendezésének számos módját. Mivel összesen 4 + 2 = 6 érme van, és ezek közül csak 3-at kell kiválasztani, az opciók teljes száma megegyezik a 6-3 kombinációk számával: C 6 3.

Meg kell találni a valószínűséget:

Ebben az esetben a b-től a-ig terjedő kombinációk számát egy képlet segítségével számítják ki, amelyet fejből kell ismerni:

Feladat. Petya zsebében 2 db 5 rubeles és 4 db 10 rubeles volt. Petya anélkül, hogy ránézett volna, áttett egy másik zsebbe 3 érmét. Határozza meg annak valószínűségét, hogy az ötrubeles érmék most különböző zsebekben vannak.

Ahhoz, hogy az ötrubeles érméket különböző zsebekben tartsa, csak az egyiket kell mozgatnia. Ennek a módjai megegyeznek a 2:1 kombinációk számával: C 2 1.

Mivel Petya összesen 3 érmét mozgott meg, további 2, egyenként 10 rubeles érmét kell mozgatnia. Petyának 4 ilyen érméje van, tehát az utak száma megegyezik a 4 x 2 kombinációk számával: C 4 2.

Már csak azt kell kideríteni, hogy hány lehetőség van a 6 elérhető érméből 3 érme átutalására. Ez a mennyiség az előző feladathoz hasonlóan megegyezik a 6 x 3 kombinációk számával: C 6 3.

Megtaláljuk a valószínűséget:

Az utolsó lépésben megszoroztuk a kétrubeles érmék és a tízrubeles érmék kiválasztásának lehetőségeinek számát, mivel ezek az események függetlenek.

Megjegyzem, a valószínűségek összege 0,4 + 0,6 = 1. Valójában az érmék száma mindkét feladatban azonos, és két érme lehet ugyanabban a zsebben vagy különböző - van nincs harmadik lehetőség.

Ez a tény megerősíti a válaszok helyességét, de a megoldás korántsem triviálisnak bizonyult, és nagyon jó valószínűségszámítási ismereteket igényel. A legtöbb iskolásnak nincs ilyen tudása.

Megjegyzések a C részhez

A C1 feladatot, amely egy összetett trigonometrikus egyenlet megoldását kéri, kissé újrafogalmazták, és most két pontból áll:

1. Valójában oldjon meg egy trigonometrikus egyenletet;
2. Keresse meg az adott szegmenshez tartozó gyökereket!

A fennmaradó feladatok gyakorlatilag változtatás nélkül átkerültek az előző próba-Egységes Államvizsgáról. A C6 feladat ugyanolyan egyszerű marad, és nem hasonlítható össze a valódi C6-okkal, amelyek a matematika egységes államvizsgájában találhatók.

A körök körültekintőbb megközelítést igényelnek, és sokkal ritkábban fordulnak elő a B5 feladatokban. Ugyanakkor az általános megoldási séma még egyszerűbb, mint a sokszögek esetében (lásd „Sokszögek területei koordináta-rácson”).

Az ilyen feladatokhoz csak az R kör sugarát kell megtalálni. Ezután kiszámíthatja a kör területét az S = πR 2 képlettel. Ebből a képletből az is következik, hogy a megoldáshoz elegendő R2-t találni.

A kijelzett értékek megtalálásához elegendő egy olyan pontot megjelölni a körön, amely a rácsvonalak metszéspontjában található. És akkor használja a Pitagorasz-tételt. Nézzünk konkrét példákat a sugár kiszámítására:

Feladat. Keresse meg az ábrán látható három kör sugarát:

Végezzünk további konstrukciókat minden körben:

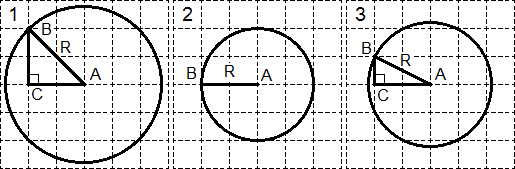
Minden esetben a B pontot választjuk a körön, hogy a rácsvonalak metszéspontjában legyen. Az 1. és 3. körben lévő C pont egészítse ki az ábrát derékszögű háromszöggé. Meg kell találni a sugarakat:

Tekintsük az ABC háromszöget az első körben. A Pitagorasz-tétel szerint: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.

A második körre minden nyilvánvaló: R = AB = 2.

A harmadik eset hasonló az elsőhöz. Az ABC háromszögből a Pitagorasz-tétel segítségével: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.

Most már tudjuk, hogyan találjuk meg a kör sugarát (vagy legalábbis a négyzetét). Ezért meg tudjuk találni a területet. Vannak olyan problémák, amikor egy szektor területét kell megtalálnia, nem pedig a teljes kört. Ilyenkor könnyen kideríthető, hogy a kör melyik része ez a szektor, és így meg lehet találni a területet.

Feladat. Keresse meg az árnyékolt szektor S területét. Kérjük, válaszában jelölje meg az S/π-t.

Nyilvánvaló, hogy a szektor egy negyed kör. Ezért S = 0,25 S kör.

Meg kell találni a kör S-jét - a kör területét. Ehhez további konstrukciót végzünk:

Az ABC háromszög derékszögű háromszög. A Pitagorasz-tétel szerint a következőt kapjuk: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.

Most megtaláljuk a kör és a szektor területét: S kör = πR 2 = 8π ; S = 0,25 S kör = 2π.

Végül a kívánt érték S /π = 2.

Ismeretlen sugarú szektorterület

Ez egy teljesen új típusú feladat, 2010-2011-ben nem volt hasonló. A feltétel szerint egy bizonyos terület kört kapunk (nevezetesen a területet, nem a sugarat!). Ezután ezen a körön belül kiválasztunk egy szektort, amelynek területét meg kell találni.

A jó hír az, hogy ezek a feladatok a legkönnyebbek a matematika egységes államvizsgán megjelenő területfeladatok közül. Ezenkívül a kör és a szektor mindig egy koordináta-rácsra kerül. Ezért az ilyen problémák megoldásának megtanulásához nézze meg a képet:

Legyen az eredeti kör S = 80 területű. Ekkor két S = 40 területű szektorra osztható (lásd 2. lépés). Hasonlóképpen, mindegyik „feles” szektor újra felezhető – négy szektort kapunk, amelyek mindegyike S = 20 területű (lásd a 3. lépést). Végül mindegyik szektort két további részre oszthatjuk - 8 „selejt” szektort kapunk. Ezen „hulladékok” területe S = 10 lesz.

Figyelem: a matematika egységes államvizsga-feladataiban nincs finomabb felosztás! Így a B-3 feladat megoldásának algoritmusa a következő:

1. Vágja fel az eredeti kört 8 „törmelék” szektorra. Mindegyik területe pontosan a teljes kör területének 1/8-a. Például, ha a feltétel szerint a kör S területe = 240, akkor a „hulladékok” területe S = 240: 8 = 30;
2. Nézze meg, hány „hulladék” fér bele az eredeti szektorba, amelynek területét meg kell találni. Például, ha a mi szektorunkban 3 darab 30 területű „selejtet” van, akkor a kívánt szektor területe S = 3 · 30 = 90. Ez lesz a válasz.

Ennyi! A probléma gyakorlatilag szóban megoldódik. Ha valami még mindig nem tiszta, vegyen egy pizzát, és vágja 8 részre. Minden ilyen darab ugyanaz a szektor-"hulladék" lesz, amelyeket nagyobb darabokra lehet kombinálni.

Most nézzünk példákat az egységesített államvizsga próbaverziójából:

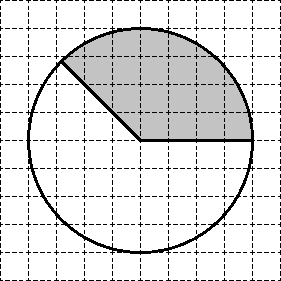
Feladat. Egy kockás papírra rajzolunk egy kört, amelynek területe 40. Keresse meg az árnyékolt ábra területét.

Tehát a kör területe 40. Osszuk fel 8 szektorra - mindegyik S = 40 területű: 5 = 8. Kapjuk:

Nyilvánvaló, hogy az árnyékolt szektor pontosan két „törmelék” szektorból áll. Ezért a területe 2 · 5 = 10. Ez a teljes megoldás!

Feladat. Egy kockás papírra rajzolunk egy kört, amelynek területe 64. Keresse meg az árnyékolt ábra területét.

Ismét oszd fel az egész kört 8 egyenlő szektorra. Nyilvánvaló, hogy az egyik területét pontosan meg kell találni. Ezért a területe S = 64: 8 = 8.

Feladat. Egy kockás papírra rajzolunk egy kört, amelynek területe 48. Keresse meg az árnyékolt ábra területét.

Ismét osszuk fel a kört 8 egyenlő szektorra. Mindegyik területe egyenlő S = 48: 8 = 6. A szükséges szektor pontosan három szektort tartalmaz - „selejteket” (lásd az ábrát). Ezért a szükséges szektor területe 3 6 = 18.

Sziasztok barátok!Benne van a matematika egységes államvizsgántartalmazza a kör területének vagy részei (szektor, gyűrűelemek) megtalálásával kapcsolatos feladatokat. A figura kockás mintával egy papírlapra van állítva. Egyes feladatokban a cella léptékét 1 × 1 centiméterben adják meg, másokban nincs megadva - a kör elemének vagy magának a körnek a területe van megadva.

A feladatok nem mélyek, emlékeznie kell a kör területének képletére, képesnek kell lennie vizuálisan (cellák alapján) meghatározni a kör sugarát, a körnek mekkora hányada van a kiválasztott szektorban. Egyébként az ágazat területéről szóló blogon. Tartalmának semmi köze az alábbiakban bemutatott problémák megoldásához, de azok számára, akik emlékezni akarnak a kör területére és egy szektor területére, nagyon hasznos lesz. Tekintsük a feladatokat (a nyílt feladatbankból):

Keresse meg (cm 2-ben) az 1 cm x 1 cm cellaméretű, kockás papíron ábrázolt ábra S területét. Írjon S/l-t válaszába!

Egy alak (gyűrű) területének megszerzéséhez ki kell vonni egy 1 sugarú kör területét a 2 sugarú kör területéből. egy kör a következő:

Eszközök,

Ossza el az eredményt Pi-vel, és írja le a választ.

Válasz: 3

Kockás papírra két kört rajzolunk. A belső kör területe 51. Keresse meg az árnyékolt ábra területét.

Az árnyékolt ábra területét a nagyobb kör területe és a kisebb kör területe közötti különbség kiszámításával találhatja meg. Határozzuk meg, hogy a nagyobb területe hányszor tér el a kisebb területétől. Legyen a kisebbik sugara egyenlő R-vel, akkor a területe egyenlő:

A nagyobb kör sugara kétszer akkora (a cellák által látható). Tehát a területe egyenlő:

Megállapítottuk, hogy területe 4-szer nagyobb.

Ezért egyenlő: 51∙4 = 204 cm 2

Így az árnyékolt ábra területe 204 – 51 = 153 cm 2.

*Második módszer. Ki lehetett számítani a kis kör sugarát, majd meghatározni a nagyobb kör sugarát. Ezután keresse meg a nagyobb területét, és számítsa ki a kívánt ábra területét.

Kockás papírra két kört rajzolunk. A belső kör területe 1. Keresse meg az árnyékolt ábra területét.

Ez a probléma gyakorlatilag megoldásában nem különbözik az előzőtől, a különbség csak annyi, hogy a köröknek más a középpontja.

Annak ellenére, hogy jól látható, hogy a nagyobb kör sugara 2-szer nagyobb, mint a kisebbé, azt tanácsolom, hogy a cella méretét az x (x) változóval jelölje meg.

Az előző feladathoz hasonlóan határozzuk meg, hogy a nagyobb területe hányszor tér el a kisebb területétől. Adjuk meg a kisebb kör területét, mivel a sugara 3x:

Adjuk meg a nagyobb kör területét, mivel a sugara 6x:

Mint látható, a nagyobb kör területe 4-szer nagyobb.

Ezért egyenlő 1∙4 = 4 cm 2

Így az árnyékolt ábra területe 4 – 1 = 3 cm 2.

Válasz: 3

Kockás papírra két kört rajzolunk. A belső kör területe 9. Keresse meg az árnyékolt ábra területét.

Jelöljük a cella méretét az x (x) változóval.

Határozzuk meg, hogy a nagyobb kör területe hányszor tér el a kisebb területétől. Határozzuk meg a kisebb kör területét. Mivel a sugara 3∙ x, akkor

Adjuk meg a nagyobb kör területét. Mivel a sugara 4∙ x, akkor

Ossza el a nagyobb területét a kisebb területével:

Vagyis a nagyobb kör területe 16/9-szerese a kisebbé, tehát egyenlő:

Így az árnyékolt ábra területe 16-9 = 7 cm 2.

*Második módszer.

Számítsuk ki a kisebb kör sugarát! Területe 9, ami azt jelenti

Határozzuk meg a cella méretét, majd meg tudjuk határozni a nagyobb kör sugarát. A cella mérete:

Mivel a nagyobb kör sugara 4 cellának felel meg, a sugara egyenlő lesz:

Határozza meg a nagyobb kör területét:

Keresse meg a különbséget: 16 – 9 = 7 cm 2

Válasz: 7

Egy 48-as kört rajzolunk a kockás papírra. Keresse meg az árnyékolt szektor területét.

Ebben a feladatban nyilvánvaló, hogy az árnyékolt rész a teljes kör területének fele, azaz egyenlő 24-gyel.

Válasz: 24

Egy rövid összefoglaló.

A kör szektorának területével kapcsolatos problémáknál meg kell tudni határozni, hogy ez mekkora hányadát teszi ki a kör területének. Ezt nem nehéz megtenni, mivel ilyen problémák esetén a szektor középponti szöge 30 vagy 45 többszöröse.

A gyűrűelemek területeinek megtalálásával kapcsolatos feladatokban különböző megoldási módok léteznek, mindkettő a megoldott feladatokban látható. Univerzálisabb az a módszer, amelyben az x változón keresztül jelzik a cella méretét, majd meghatározzák a sugarakat.

De a legfontosabb dolog az, hogy ne memorizáljuk ezeket a módszereket. Találhatsz egy harmadik és negyedik megoldást is. A lényeg az, hogy ismerje a kör területének képletét, és tudjon logikusan érvelni.

Ez minden. Sok sikert neked!

P.S.: Hálás lennék, ha mesélne az oldalról a közösségi oldalakon.