Az y x függvény tulajdonságai 2. Függvények és tulajdonságaik

Bemutatjuk a hatványfüggvények tulajdonságait és grafikonjait a kitevő különböző értékeire. Alapképletek, definíciós tartományok és értékkészletek, paritás, monotonitás, növekvő és csökkenő, szélsőségek, konvexitás, inflexiók, metszéspontok koordinátatengelyekkel, határértékek, konkrét értékek.

Képletek hatványfüggvényekkel

Az y = x p hatványfüggvény definíciós tartományában a következő képletek érvényesek:
; ;
;
; ;
; ;
; .

Hatványfüggvények tulajdonságai és grafikonjaik

Hatványfüggvény nullával egyenlő kitevővel, p = 0

Ha az y = x p hatványfüggvény kitevője nulla, p = 0, akkor a hatványfüggvény minden x ≠ 0 esetén definiálva van, és eggyel egyenlő állandó:
y = x p = x 0 = 1, x ≠ 0.

Hatványfüggvény természetes páratlan kitevővel, p = n = 1, 3, 5, ...

Tekintsünk egy y = x p = x n hatványfüggvényt, amelynek természetes páratlan kitevője n = 1, 3, 5, ... . Ez a mutató a következő formában is felírható: n = 2k + 1, ahol k = 0, 1, 2, 3, ... egy nem negatív egész szám. Az alábbiakban az ilyen függvények tulajdonságait és grafikonjait mutatjuk be.

Egy y = x n hatványfüggvény grafikonja természetes páratlan kitevővel az n = 1, 3, 5, ... kitevő különböző értékeire.

Tartomány: -∞ < x < ∞
Több jelentése: -∞ < y < ∞
Paritás: páratlan, y(-x) = - y(x)
Monoton: monoton növekszik
Extrémek: Nem
Konvex:
-∞-nél< x < 0 выпукла вверх
0-nál< x < ∞ выпукла вниз
Inflexiós pontok: x = 0, y = 0
x = 0, y = 0
Korlátok:
;
Privát értékek:
x = -1-nél,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
x = 0 esetén y(0) = 0 n = 0
ha x = 1, y(1) = 1 n = 1
Fordított funkció:
n = 1 esetén a függvény az inverze: x = y
n ≠ 1 esetén az inverz függvény az n fok gyöke:

Hatványfüggvény természetes páros kitevővel, p = n = 2, 4, 6, ...

Tekintsünk egy y = x p = x n hatványfüggvényt, amelynek természetes páros kitevője n = 2, 4, 6, ... . Ez a mutató a következő formában is felírható: n = 2k, ahol k = 1, 2, 3, ... - természetes. Az alábbiakban az ilyen függvények tulajdonságait és grafikonjait mutatjuk be.

Egy y = x n hatványfüggvény grafikonja természetes páros kitevővel az n = 2, 4, 6, ... kitevő különböző értékeire.

Tartomány: -∞ < x < ∞
Több jelentése: 0 ≤ év< ∞
Paritás: páros, y(-x) = y(x)
Monoton:
x ≤ 0 esetén monoton csökken
x ≥ 0 esetén monoton növekszik
Extrémek: minimum, x = 0, y = 0
Konvex: lefelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Korlátok:
;
Privát értékek:
x = -1-nél, y(-1) = (-1) n ≡ (-1) 2k = 1
x = 0 esetén y(0) = 0 n = 0
ha x = 1, y(1) = 1 n = 1
Fordított funkció:
n = 2 esetén négyzetgyök:
n ≠ 2 esetén az n fok gyöke:

Hatványfüggvény negatív egész kitevővel, p = n = -1, -2, -3, ...

Tekintsünk egy y = x p = x n hatványfüggvényt, amelynek egész szám negatív kitevője n = -1, -2, -3, ... . Ha n = -k-t teszünk, ahol k = 1, 2, 3, ... egy természetes szám, akkor a következőképpen ábrázolható:

Egy y = x n hatványfüggvény grafikonja negatív egész kitevővel az n = -1, -2, -3, ... kitevő különböző értékeire.

Páratlan kitevő, n = -1, -3, -5, ...

Az alábbiakban az y = x n függvény tulajdonságait mutatjuk be páratlan negatív kitevővel, n = -1, -3, -5, ....

Tartomány: x ≠ 0
Több jelentése: y ≠ 0
Paritás: páratlan, y(-x) = - y(x)
Monoton: monoton csökken
Extrémek: Nem
Konvex:
x-nél< 0 : выпукла вверх
x > 0 esetén: konvex lefelé
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: Nem
Jel:
x-nél< 0, y < 0
ha x > 0, y > 0
Korlátok:
; ; ;
Privát értékek:
ha x = 1, y(1) = 1 n = 1
Fordított funkció:
ha n = -1,
a n< -2 ,

Páros kitevő, n = -2, -4, -6, ...

Alább láthatók az y = x n függvény tulajdonságai, páros negatív kitevőjű n = -2, -4, -6, ....

Tartomány: x ≠ 0
Több jelentése: y > 0
Paritás: páros, y(-x) = y(x)
Monoton:
x-nél< 0 : монотонно возрастает
x > 0 esetén: monoton csökken
Extrémek: Nem
Konvex: lefelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: Nem
Jel: y > 0
Korlátok:
; ; ;
Privát értékek:
ha x = 1, y(1) = 1 n = 1
Fordított funkció:
n = -2-nél,
a n< -2 ,

Hatványfüggvény racionális (tört) kitevővel

Tekintsünk egy racionális (tört) kitevővel rendelkező y = x p hatványfüggvényt, ahol n egész szám, m > 1 természetes szám. Ráadásul n-nek, m-nek nincs közös osztója.

A törtmutató nevezője páratlan

Legyen a törtkitevő nevezője páratlan: m = 3, 5, 7, ... . Ebben az esetben az x p hatványfüggvény az x argumentum pozitív és negatív értékeire egyaránt definiálva van. Tekintsük az ilyen hatványfüggvények tulajdonságait, ha a p kitevő bizonyos határokon belül van.

A p-érték negatív, p< 0

Legyen a racionális kitevő (m = 3, 5, 7, ... páratlan nevezővel) kisebb nullánál: .

Hatványfüggvények grafikonjai racionális negatív kitevővel a kitevő különböző értékeire, ahol m = 3, 5, 7, ... - páratlan.

Páratlan számláló, n = -1, -3, -5, ...

Az y = x p hatványfüggvény tulajdonságait racionális negatív kitevővel mutatjuk be, ahol n = -1, -3, -5, ... páratlan negatív egész szám, m = 3, 5, 7 ... egy páratlan természetes egész szám.

Tartomány: x ≠ 0
Több jelentése: y ≠ 0
Paritás: páratlan, y(-x) = - y(x)
Monoton: monoton csökken
Extrémek: Nem
Konvex:
x-nél< 0 : выпукла вверх
x > 0 esetén: konvex lefelé
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: Nem
Jel:
x-nél< 0, y < 0
ha x > 0, y > 0
Korlátok:
; ; ;
Privát értékek:
x = -1 esetén y(-1) = (-1) n = -1
ha x = 1, y(1) = 1 n = 1
Fordított funkció:

Páros számláló, n = -2, -4, -6, ...

Az y = x p hatványfüggvény tulajdonságai racionális negatív kitevővel, ahol n = -2, -4, -6, ... páros negatív egész szám, m = 3, 5, 7 ... páratlan természetes egész szám .

Tartomány: x ≠ 0
Több jelentése: y > 0
Paritás: páros, y(-x) = y(x)
Monoton:
x-nél< 0 : монотонно возрастает
x > 0 esetén: monoton csökken
Extrémek: Nem
Konvex: lefelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: Nem
Jel: y > 0
Korlátok:
; ; ;
Privát értékek:
x = -1 esetén y(-1) = (-1) n = 1
ha x = 1, y(1) = 1 n = 1
Fordított funkció:

A p-érték pozitív, kisebb, mint egy, 0< p < 1

Hatványfüggvény grafikonja racionális kitevővel (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.

Páratlan számláló, n = 1, 3, 5, ...

< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Tartomány: -∞ < x < +∞
Több jelentése: -∞ < y < +∞
Paritás: páratlan, y(-x) = - y(x)
Monoton: monoton növekszik
Extrémek: Nem
Konvex:
x-nél< 0 : выпукла вниз
x > 0 esetén: konvex felfelé
Inflexiós pontok: x = 0, y = 0
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Jel:
x-nél< 0, y < 0
ha x > 0, y > 0
Korlátok:
;
Privát értékek:
x = -1 esetén y(-1) = -1
x = 0 esetén y(0) = 0
x = 1 esetén y(1) = 1
Fordított funkció:

Páros számláló, n = 2, 4, 6, ...

Bemutatjuk az y = x p hatványfüggvény tulajdonságait 0-n belüli racionális kitevővel< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Tartomány: -∞ < x < +∞
Több jelentése: 0 ≤ év< +∞
Paritás: páros, y(-x) = y(x)
Monoton:
x-nél< 0 : монотонно убывает
x > 0 esetén: monoton növekszik
Extrémek: minimum x = 0, y = 0
Konvex: felfelé konvex x ≠ 0 esetén
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Jel: x ≠ 0 esetén y > 0
Korlátok:
;
Privát értékek:
x = -1 esetén y(-1) = 1
x = 0 esetén y(0) = 0
x = 1 esetén y(1) = 1
Fordított funkció:

A p index nagyobb egynél, p > 1

Egy hatványfüggvény grafikonja racionális kitevővel (p > 1) a kitevő különböző értékeire, ahol m = 3, 5, 7, ... - páratlan.

Páratlan számláló, n = 5, 7, 9, ...

Az y = x p hatványfüggvény tulajdonságai egynél nagyobb racionális kitevővel: . Ahol n = 5, 7, 9, ... - páratlan természetes, m = 3, 5, 7 ... - páratlan természetes.

Tartomány: -∞ < x < ∞
Több jelentése: -∞ < y < ∞
Paritás: páratlan, y(-x) = - y(x)
Monoton: monoton növekszik
Extrémek: Nem
Konvex:
-∞-nél< x < 0 выпукла вверх
0-nál< x < ∞ выпукла вниз
Inflexiós pontok: x = 0, y = 0
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Korlátok:
;
Privát értékek:
x = -1 esetén y(-1) = -1
x = 0 esetén y(0) = 0
x = 1 esetén y(1) = 1
Fordított funkció:

Páros számláló, n = 4, 6, 8, ...

Az y = x p hatványfüggvény tulajdonságai egynél nagyobb racionális kitevővel: . Ahol n = 4, 6, 8, ... - páros természetes, m = 3, 5, 7 ... - páratlan természetes.

Tartomány: -∞ < x < ∞
Több jelentése: 0 ≤ év< ∞
Paritás: páros, y(-x) = y(x)
Monoton:
x-nél< 0 монотонно убывает
x > 0 esetén monoton növekszik
Extrémek: minimum x = 0, y = 0
Konvex: lefelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Korlátok:
;
Privát értékek:
x = -1 esetén y(-1) = 1
x = 0 esetén y(0) = 0
x = 1 esetén y(1) = 1
Fordított funkció:

A törtmutató nevezője páros

Legyen a törtkitevő nevezője páros: m = 2, 4, 6, ... . Ebben az esetben az x p hatványfüggvény nincs megadva az argumentum negatív értékeihez. Tulajdonságai egybeesnek egy irracionális kitevővel rendelkező hatványfüggvény tulajdonságaival (lásd a következő részt).

Hatványfüggvény irracionális kitevővel

Tekintsünk egy y = x p hatványfüggvényt p irracionális kitevőjével. Az ilyen függvények tulajdonságai abban különböznek a fentebb tárgyaltaktól, hogy nincsenek meghatározva az x argumentum negatív értékeihez. Az argumentum pozitív értékei esetén a tulajdonságok csak a p kitevő értékétől függenek, és nem függenek attól, hogy p egész szám, racionális vagy irracionális.

y = x p a p kitevő különböző értékeihez.

Hatványfüggvény negatív kitevővel p< 0

Tartomány: x > 0
Több jelentése: y > 0
Monoton: monoton csökken
Konvex: lefelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: Nem
Korlátok: ;
Privát jelentése: Ha x = 1, y(1) = 1 p = 1

Hatványfüggvény pozitív kitevővel p > 0

A mutató kevesebb, mint egy 0< p < 1

Tartomány: x ≥ 0
Több jelentése: y ≥ 0
Monoton: monoton növekszik
Konvex: felfelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Korlátok:
Privát értékek: Ha x = 0, y(0) = 0 p = 0.
Ha x = 1, y(1) = 1 p = 1

A mutató nagyobb, mint egy p > 1

Tartomány: x ≥ 0
Több jelentése: y ≥ 0
Monoton: monoton növekszik
Konvex: lefelé domború
Inflexiós pontok: Nem
Metszéspontok koordinátatengelyekkel: x = 0, y = 0
Korlátok:
Privát értékek: Ha x = 0, y(0) = 0 p = 0.
Ha x = 1, y(1) = 1 p = 1

Referenciák:
BAN BEN. Bronstein, K.A. Semendyaev, Matematika kézikönyve mérnökök és főiskolai hallgatók számára, „Lan”, 2009.

A rész referenciaanyagot tartalmaz a fő elemi függvényekről és tulajdonságaikról. Adott az elemi függvények osztályozása. Az alábbiakban linkek találhatók olyan alszakaszokhoz, amelyek konkrét függvények tulajdonságait tárgyalják – grafikonok, képletek, deriváltak, antideriválták (integrálok), sorozatbővítések, kifejezések összetett változókon keresztül.

Az alapvető funkciók referenciaoldalai

Az elemi függvények osztályozása

Algebrai függvény olyan függvény, amely kielégíti a következő egyenletet:
,
ahol polinom az y függő változóban és az x független változóban. Így írható:
,
hol vannak a polinomok.

Az algebrai függvényeket polinomokra (teljes racionális függvényekre), racionális függvényekre és irracionális függvényekre osztjuk.

Teljes racionális funkció, amit más néven polinom vagy polinom, az összeadás (kivonás) és szorzás aritmetikai műveleteinek segítségével az x változóból és véges számú számból adódik. A zárójelek kinyitása után a polinom kanonikus formára csökken:
.

Tört racionális függvény, vagy egyszerűen racionális funkció, az x változóból és véges számú számból az összeadás (kivonás), szorzás és osztás aritmetikai műveleteivel kapjuk meg. A racionális függvény a formára redukálható
,
ahol és vannak polinomok.

Irracionális funkció egy algebrai függvény, amely nem racionális. Az irracionális függvényen általában gyököket és azok racionális függvényekkel rendelkező összetételeit értjük. Az n fokú gyöke az egyenlet megoldása
.
A következőképpen van megjelölve:
.

Transzcendentális funkciók nem algebrai függvényeknek nevezzük. Ezek exponenciális, trigonometrikus, hiperbolikus és ezek inverz függvényei.

Az alapvető elemi funkciók áttekintése

Valamennyi elemi függvény ábrázolható véges számú összeadási, kivonási, szorzási és osztási műveletként, amelyet a forma kifejezésén hajtanak végre:
z t .
Az inverz függvények logaritmussal is kifejezhetők. Az alábbiakban felsoroljuk az alapvető elemi funkciókat.

Teljesítmény funkció:
y(x) = xp,
ahol p a kitevő. Az x fok alapjától függ.
A hatványfüggvény inverze egyben a hatványfüggvény is:
.
A p kitevő egész szám, nem negatív értéke esetén ez egy polinom. Egész p érték esetén racionális függvény. Racionális jelentéssel - irracionális funkcióval.

Transzcendentális funkciók

Exponenciális függvény :
y(x) = a x ,
ahol a a fokszám alapja. Ez az x kitevőtől függ.
Az inverz függvény a logaritmus az a alapján:
x = log a y.

Kitevő, e az x hatványra:
y(x) = e x ,
Ez egy exponenciális függvény, amelynek deriváltja magával a függvénnyel egyenlő:
.
A kitevő alapja az e szám:
≈ 2,718281828459045... .
Az inverz függvény a természetes logaritmus - az e szám alapjához tartozó logaritmus:
x = ln y ≡ log e y.

Trigonometrikus függvények:
Sine: ;
Koszinusz: ;
Érintő: ;
Kotangens: ;
Itt i a képzeletbeli egység, i 2 = -1.

Inverz trigonometrikus függvények:
Arcsine: x = arcsin y, ;
Ív koszinusz: x = arccos y, ;
Arktangens: x = arctan y, ;
Ívtangens: x = arcctg y, .

Egy függvény definíciós tartománya és értéktartománya. Az elemi matematikában a függvényeket csak valós számok halmazán tanulmányozzák R Ez azt jelenti, hogy a függvény argumentum csak azokat a valós értékeket veheti fel, amelyekre a függvény definiálva van, pl. az is csak valódi értékeket fogad el. Egy csomó x minden érvényes érvényes argumentumérték x, amelyhez a függvény y= f(x)definiált, hívott a függvény tartománya. Egy csomó Y minden valódi érték y, amelyet a függvény elfogad, hívjuk funkció tartomány. Most már pontosabban definiálhatjuk a függvényt: szabály(törvény) az X és Y halmazok közötti megfelelésről, amely szerint a halmaz egyes elemeireX egy és csak egy elemet találhat az Y halmazból, amelyet függvénynek nevezünk.

Ebből a definícióból következik, hogy egy függvény definiáltnak tekinthető, ha:

Meg van adva a függvény tartománya x ;

Meg van adva a funkciótartomány Y ;

A levelezés szabálya (törvénye) ismert, és olyan, hogy mindegyikre

Egy argumentumértékhez csak egy függvényérték található.

A funkció egyértelműségének ezen követelménye kötelező.

Monoton funkció. Ha az argumentum bármely két értékére x 1 és x 2. feltétel x 2 > x 1 következik f(x 2) > f(x 1), majd a függvényt f(x) nak, nek hívják növekvő; ha valamelyikre x 1 és x 2. feltétel x 2 > x 1 következik f(x 2) < f(x 1), majd a függvényt f(x) nak, nek hívják csökkenő. Olyan függvényt hívunk, amely csak növekszik vagy csak csökken monoton.

Korlátozott és korlátlan funkciók. A függvényt hívják korlátozott, ha van ilyen pozitív szám M milyen | f(x) | M minden értékre x. Ha ilyen szám nem létezik, akkor a függvény igen korlátlan.

PÉLDÁK.

A 3. ábrán látható funkció korlátozott, de nem monoton. A 4. ábra funkciója éppen az ellenkezője, monoton, de korlátlan. (Ezt kérem magyarázza meg!).

Folyamatos és nem folytonos funkciók. Funkció y = f (x) nak, nek hívják folyamatos azon a pontonx = a, Ha:

1) a függvényt mikor határozzuk meg x = a, azaz f (a) létezik;

2) létezik véges limit lim f (x) ;

x→a

(lásd Funkciókorlátok)

3) f (a) = lim f (x) .

x→a

Ha e feltételek közül legalább egy nem teljesül, akkor a függvény meghívásra kerül robbanó azon a ponton x = a.

Ha a funkció közben folyamatos mindenki definíciós tartományának pontjait, akkor úgy hívják folyamatos funkció.

Páros és páratlan függvények. Ha azért Bármi x f(- x) = f (x), akkor a függvény meghívásra kerül még;ha előfordul: f(- x) = - f (x), akkor a függvény meghívásra kerül páratlan. Páros függvény grafikonja szimmetrikus az Y tengelyre(5. ábra), egy páratlan függvény grafikonja Simmetrika az eredethez képest(6. ábra).

Periodikus funkció. Funkció f (x) - időszakos, ha létezik ilyen nem nulla szám T minek Bármi x a függvény definíciós tartományából a következők érvényesek: f (x + T) = f (x). Ez legkevésbé hívják a számot a funkció időszaka. Minden trigonometrikus függvény periodikus.

1. példa Bizonyítsd be ezt a bűnt x periódusa 2.

Megoldás: Tudjuk, hogy a bűn ( x+ 2n) = bűn x, Ahol n= 0, ± 1, ± 2, …

Ezért a 2. kiegészítés n nem a szinuszos érvhez

Megváltoztatja a jelentését. Van ezzel más szám is

Ugyanaz az ingatlan?

Tegyünk úgy, mintha P- ilyen szám, i.e. egyenlőség:

Bűn ( x+P) = bűn x,

Bármilyen értékre érvényes x. De akkor megvan

Hely és idő x= / 2, azaz

Bűn(/2 + P) = sin / 2 = 1.

De a redukciós képlet szerint a bűn ( / 2 + P) = cos P. Akkor

Az utolsó két egyenlőségből az következik, hogy cos P= 1, de mi

Tudjuk, hogy ez csak akkor igaz, ha P = 2n. A legkisebb óta

Nem nulla szám 2-től n 2, akkor ez a szám

És van egy időszakos bűn x. Hasonló módon igazolható, hogy a 2 tól től n, tehát ez a sin 2 periódusa x.

Funkció nullák. Meghívásra kerül az az argumentumérték, amelynél a függvény 0-val egyenlő nulla (gyökér) függvény. Egy függvénynek több nullája is lehet. Például a függvény y = x (x + 1) (x-3) három nulla van: x= 0, x= -1, x= 3. Geometriailag null függvény - ez a függvénygráf és a tengely metszéspontjának abszcisszán x .

A 7. ábra egy függvény grafikonját mutatja nullákkal: x= a, x = bÉs x= c.

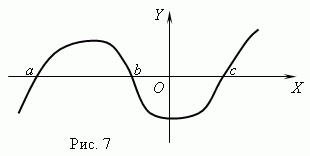
Aszimptota. Ha egy függvény gráfja korlátlanul közelít egy bizonyos egyeneshez, amikor távolodik az origótól, akkor ezt az egyenest ún. aszimptota.

1) Funkciótartomány és funkciótartomány.

Egy függvény tartománya az összes érvényes érvényes argumentumérték halmaza x(változó x), amelyhez a függvény y = f(x) eltökélt. Egy függvény tartománya az összes valós érték halmaza y, amelyet a függvény elfogad.

Az elemi matematikában a függvényeket csak valós számok halmazán tanulmányozzák.

2) Funkció nullák.

A nulla függvény annak az argumentumnak az értéke, amelynél a függvény értéke nullával egyenlő.

3) Egy függvény állandó előjelének intervallumai.

A függvény állandó előjelének intervallumai olyan argumentumértékek halmazai, amelyeken a függvényértékek csak pozitívak vagy csak negatívak.

4) A függvény monotonitása.

Növekvő függvény (egy bizonyos intervallumban) olyan függvény, amelyben ebből az intervallumból származó argumentum nagyobb értéke a függvény nagyobb értékének felel meg.

Csökkenő függvény (egy bizonyos intervallumban) olyan függvény, amelyben ebből az intervallumból származó argumentum nagyobb értéke a függvény kisebb értékének felel meg.

5) Páros (páratlan) függvény.

A páros függvény olyan függvény, amelynek definíciós tartománya szimmetrikus az origóhoz és bármely függvényhez x a definíció tartományából az egyenlőség f(-x) = f(x). A páros függvény grafikonja szimmetrikus az ordinátára.

A páratlan függvény olyan függvény, amelynek definíciós tartománya szimmetrikus az origóhoz és bármely függvényhez x a definíció tartományából az egyenlőség igaz f(-x) = - f(x). Egy páratlan függvény grafikonja szimmetrikus az origóra.

6) Korlátozott és korlátlan funkciók.

Egy függvényt korlátosnak nevezünk, ha van olyan pozitív M szám, amelyre |f(x)| ≤ M x összes értékére. Ha ilyen szám nem létezik, akkor a függvény korlátlan.

7) A függvény periodicitása.

Egy f(x) függvény periodikus, ha van egy nullától eltérő T szám, amelyre a függvény definíciós tartományából származó bármely x-re teljesül a következő: f(x+T) = f(x). Ezt a legkisebb számot a függvény periódusának nevezzük. Minden trigonometrikus függvény periodikus. (Trigonometrikus képletek).

19. Alapvető elemi függvények, tulajdonságaik és grafikonjai. Függvények alkalmazása a közgazdaságtanban.

Alapvető elemi funkciók. Tulajdonságaik és grafikonjaik

1. Lineáris függvény.

Lineáris függvény alakú függvénynek nevezzük, ahol x változó, a és b valós számok.

Szám A az egyenes meredekségének nevezzük, ez egyenlő ennek az egyenesnek az x tengely pozitív irányához viszonyított dőlésszögének érintőjével. A lineáris függvény grafikonja egy egyenes. Két pont határozza meg.

Lineáris függvény tulajdonságai

1. Definíciós tartomány - az összes valós szám halmaza: D(y)=R

2. Az értékkészlet az összes valós szám halmaza: E(y)=R

3. A függvény nulla értéket vesz fel, ha vagy.

4. A függvény növekszik (csökken) a teljes definíciós tartományban.

5. Egy lineáris függvény folytonos a teljes definíciós tartományban, differenciálható és .

2. Másodfokú függvény.

Egy olyan alakú függvényt, ahol x változó, a, b, c együtthatók valós számok, ún. négyzetes