Sistemi i ekuacioneve lineare dhe i pabarazive. Sistemet e pabarazive - informacioni bazë
Ky artikull përmban informacion fillestar për sistemet e pabarazive. Këtu është një përkufizim i një sistemi pabarazish dhe një përkufizim i një zgjidhjeje për një sistem pabarazish. Janë renditur edhe llojet kryesore të sistemeve me të cilat duhet punuar më shpesh në mësimet e algjebrës në shkollë dhe jepen shembuj.
Navigimi i faqes.
Çfarë është një sistem pabarazish?
Është e përshtatshme të përcaktohen sistemet e pabarazive në të njëjtën mënyrë siç kemi prezantuar përkufizimin e një sistemi ekuacionesh, domethënë nga lloji i shënimit dhe kuptimi i ngulitur në të.
Përkufizimi.
Sistemi i pabaraziveështë një rekord që përfaqëson një numër të caktuar pabarazish të shkruara njëra poshtë tjetrës, të bashkuar në të majtë nga një kllapa kaçurrelë dhe tregon grupin e të gjitha zgjidhjeve që janë njëkohësisht zgjidhje për çdo pabarazi të sistemit.
Le të japim një shembull të një sistemi pabarazish. Le të marrim dy arbitrare, për shembull, 2 x−3>0 dhe 5−x≥4 x−11, t'i shkruajmë njëra poshtë tjetrës
2 x−3>0,
5−x≥4 x−11
dhe bashkohemi me një shenjë sistemi - një mbajtës kaçurrelë, si rezultat marrim një sistem pabarazish të formës së mëposhtme:
Një ide e ngjashme jepet për sistemet e pabarazive në tekstet shkollore. Vlen të theksohet se përkufizimet e tyre janë dhënë më ngushtë: për pabarazitë me një ndryshore ose me dy variabla.
Llojet kryesore të sistemeve të pabarazive
Është e qartë se dikush mund të kompozojë pafundësisht shumë sisteme të ndryshme pabarazitë Për të mos humbur në këtë larmi, këshillohet t'i konsideroni ato në grupe që kanë të tyren veçoritë. Të gjitha sistemet e pabarazive mund të ndahen në grupe sipas kritereve të mëposhtme:
- nga numri i pabarazive në sistem;
- nga numri i variablave të përfshirë në regjistrim;
- nga vetë lloji i pabarazive.
Në bazë të numrit të pabarazive të përfshira në procesverbal, dallohen sistemet me dy, tre, katër etj. pabarazitë Në paragrafin e mëparshëm dhamë një shembull të një sistemi, i cili është një sistem me dy pabarazi. Le të tregojmë një shembull tjetër të një sistemi me katër pabarazi  .
.
Më vete, do të themi se nuk ka kuptim të flasim për një sistem të një pabarazie, në këtë rast, në thelb ne po flasim për për vetë pabarazinë, jo për sistemin.
Nëse shikoni numrin e variablave, atëherë ekzistojnë sisteme të pabarazive me një, dy, tre, etj. variablat (ose, siç thonë edhe ata, të panjohurat). Shikoni sistemin e fundit të pabarazive të shkruar dy paragrafë më lart. Është një sistem me tre variabla x, y dhe z. Ju lutemi vini re se dy pabarazitë e saj të para nuk përmbajnë të tre variablat, por vetëm njërën prej tyre. Në kontekstin e këtij sistemi, ato duhen kuptuar si pabarazi me tre variablat e formës x+0·y+0·z≥−2 dhe 0·x+y+0·z≤5 përkatësisht. Vini re se shkolla fokusohet në pabarazitë me një ndryshore.
Mbetet për të diskutuar se cilat lloje të pabarazive përfshihen në sistemet e regjistrimit. Në shkollë, ata konsiderojnë kryesisht sistemet e dy pabarazive (më rrallë - tre, madje më rrallë - katër ose më shumë) me një ose dy ndryshore, dhe vetë pabarazitë zakonisht janë pabarazi të tëra shkalla e parë ose e dytë (më rrallë - më shumë shkallë të lartë ose pjesërisht racionale). Por mos u habitni nëse në materialet tuaja përgatitore për Provimin e Bashkuar të Shtetit hasni sisteme pabarazish që përmbajnë pabarazi iracionale, logaritmike, eksponenciale dhe të tjera. Si shembull, japim sistemin e pabarazive  , është marrë nga .
, është marrë nga .
Cila është zgjidhja e një sistemi pabarazish?
Le të prezantojmë një përkufizim tjetër në lidhje me sistemet e pabarazive - përkufizimi i një zgjidhjeje për një sistem pabarazish:
Përkufizimi.
Zgjidhja e një sistemi pabarazish me një ndryshore quhet një vlerë e tillë e një ndryshoreje që e kthen secilën nga pabarazitë e sistemit në të vërtetë, me fjalë të tjera, është një zgjidhje për çdo pabarazi të sistemit.
Le të shpjegojmë me një shembull. Le të marrim një sistem me dy pabarazi me një ndryshore. Le të marrim vlerën e ndryshores x të barabartë me 8, ajo është një zgjidhje për sistemin tonë të pabarazive sipas definicionit, pasi zëvendësimi i saj në inekuacionet e sistemit jep dy inekuacione numerike të sakta 8>7 dhe 2−3·8≤0. Përkundrazi, uniteti nuk është një zgjidhje për sistemin, pasi kur zëvendësohet me ndryshoren x, pabarazia e parë do të bëhet e pasaktë. pabarazia numerike 1>7 .
Në mënyrë të ngjashme, mund të prezantohet përkufizimi i një zgjidhjeje për një sistem pabarazish me dy, tre dhe një numër i madh variablat:
Përkufizimi.
Zgjidhja e një sistemi pabarazish me dy, tre etj. variablave quhet një çift, tre etj. vlerat e këtyre variablave, që në të njëjtën kohë është një zgjidhje për çdo pabarazi të sistemit, pra e kthen çdo pabarazi të sistemit në një pabarazi numerike të saktë.
Për shembull, një çift vlerash x=1, y=2 ose në një shënim tjetër (1, 2) është një zgjidhje për një sistem pabarazish me dy ndryshore, pasi 1+2<7 и 1−2<0 - верные числовые неравенства. А пара (3,5, 3) не является решением этой системы, так как второе неравенство при этих значениях переменных дает неверное числовое неравенство 3,5−3<0 .
Sistemet e pabarazive mund të mos kenë zgjidhje, mund të kenë një numër të kufizuar zgjidhjesh ose mund të kenë një numër të pafund zgjidhjesh. Njerëzit shpesh flasin për grupin e zgjidhjeve të një sistemi pabarazish. Kur një sistem nuk ka zgjidhje, atëherë ka një grup të zbrazët të zgjidhjeve të tij. Kur ka një numër të kufizuar zgjidhjesh, atëherë bashkësia e zgjidhjeve përmban një numër të kufizuar elementësh, dhe kur ka pafundësisht shumë zgjidhje, atëherë bashkësia e zgjidhjeve përbëhet nga një numër i pafund elementësh.
Disa burime paraqesin përkufizime të një zgjidhjeje të veçantë dhe të përgjithshme për një sistem pabarazish, si për shembull, në tekstet shkollore të Mordkovich. Nën zgjidhje private e sistemit të pabarazive kuptoni një vendim të vetëm të saj. Nga ana e saj zgjidhje e përgjithshme e sistemit të pabarazive- këto janë të gjitha vendimet e saj private. Sidoqoftë, këto terma kanë kuptim vetëm kur është e nevojshme të theksohet në mënyrë specifike për çfarë lloj zgjidhjeje po flasim, por zakonisht kjo është tashmë e qartë nga konteksti, kështu që shumë më shpesh ata thjesht thonë "një zgjidhje për një sistem pabarazish".
Nga përkufizimet e një sistemi pabarazish dhe zgjidhjet e tij të paraqitura në këtë artikull, rezulton se një zgjidhje për një sistem pabarazish është kryqëzimi i grupeve të zgjidhjeve për të gjitha pabarazitë e këtij sistemi.
Bibliografi.
- Algjebra: teksti shkollor për klasën e 8-të. arsimi i përgjithshëm institucionet / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; e Redaktuar nga S. A. Telyakovsky. - botimi i 16-të. - M.: Arsimi, 2008. - 271 f. : i sëmurë. - ISBN 978-5-09-019243-9.
- Algjebra: Klasa e 9-të: arsimore. për arsimin e përgjithshëm institucionet / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; e Redaktuar nga S. A. Telyakovsky. - botimi i 16-të. - M.: Arsimi, 2009. - 271 f. : i sëmurë. - ISBN 978-5-09-021134-5.
- Mordkovich A.G. Algjebër. klasa e 9-të. Në 2 orë Pjesa 1. Libër shkollor për studentët e institucioneve të arsimit të përgjithshëm / A. G. Mordkovich, P. V. Semenov. - Botimi i 13-të, i fshirë. - M.: Mnemosyne, 2011. - 222 f.: ill. ISBN 978-5-346-01752-3.
- Mordkovich A.G. Algjebra dhe fillimi i analizës matematikore. Klasa 11. Në 2 pjesë. Pjesa 1. Libër shkollor për studentët e institucioneve të arsimit të përgjithshëm (niveli i profilit) / A. G. Mordkovich, P. V. Semenov. - Botimi i 2-të, i fshirë. - M.: Mnemosyne, 2008. - 287 f.: ill. ISBN 978-5-346-01027-2.
- Provimi i Unifikuar i Shtetit-2013. Matematika: opsionet standarde të provimit: 30 opsione / ed. A. L. Semenova, I. V. Yashchenko. – M.: Shtëpia Botuese “Arsimi Kombëtar”, 2012. – 192 f. – (USE-2013. FIPI - shkolla).
Metoda grafike.. 3
Metoda e thjeshtë.. 6
Metoda e bazës artificiale... 8
Parimi i dualitetit.. 10
Lista e literaturës së përdorur... 12
Prezantimi
Disa veti të sistemeve të pabarazive lineare u konsideruan në gjysmën e parë të shekullit të 19-të në lidhje me disa probleme të mekanikës analitike. Studimi sistematik i sistemeve të pabarazive lineare filloi në fund të shekullit të 19-të, por u bë e mundur të flitej për teorinë e pabarazive lineare vetëm në fund të viteve njëzetë të shekullit të 20-të, kur një numër i mjaftueshëm rezultatesh në lidhje me to kishte tashmë të grumbulluara.
Tani teoria e sistemeve të fundme të pabarazive lineare mund të konsiderohet si një degë e algjebrës lineare, e cila u rrit prej saj me kërkesën shtesë të renditjes së fushës së koeficientëve.
Pabarazitë lineare janë veçanërisht të rëndësishme për ekonomistët, sepse është me ndihmën e pabarazive lineare që mund të modelohen proceset e prodhimit dhe të gjenden planet më fitimprurëse për prodhimin, transportin, shpërndarjen e burimeve, etj.
Ky punim do të përshkruajë metodat bazë për zgjidhjen e pabarazive lineare të aplikuara për probleme specifike.
Metoda grafike
Metoda grafike konsiston në ndërtimin e një grupi zgjidhjesh të pranueshme për PLP, dhe gjetjen në këtë grup të pikës që korrespondon me funksionin objektiv maksimal/min.
Për shkak të mundësive të kufizuara të paraqitjes grafike vizuale, kjo metodë përdoret vetëm për sistemet e pabarazive lineare me dy të panjohura dhe sisteme që mund të reduktohen në këtë formë.
Për të demonstruar qartë metodën grafike, le të zgjidhim problemin e mëposhtëm:
- Në fazën e parë, është e nevojshme të ndërtohet një rajon zgjidhjesh të realizueshme. Për këtë shembull, është më e përshtatshme të zgjidhni X2 si abshisë, dhe X1 si ordinatë, dhe të shkruani pabarazitë në formën e mëposhtme:
 si grafikët ashtu edhe zona e zgjidhjeve të realizueshme janë në tremujorin e parë.
si grafikët ashtu edhe zona e zgjidhjeve të realizueshme janë në tremujorin e parë. Për të gjetur pikat kufitare, zgjidhim ekuacionet (1)=(2), (1)=(3) dhe (2)=(3).

Siç mund të shihet nga ilustrimi, poliedri ABCDE formon një rajon zgjidhjesh të realizueshme.
Nëse rajoni i zgjidhjeve të realizueshme nuk është i mbyllur, atëherë ose max(f)=+ ∞ ose min(f)= -∞.
- Tani mund të vazhdojmë drejt gjetjes së maksimumit të funksionit f.
Duke zëvendësuar në mënyrë alternative koordinatat e kulmeve të poliedrit në funksionin f dhe duke krahasuar vlerat, gjejmë se
f(C)=f(4;1)=19 – maksimumi i funksionit.
Kjo qasje është mjaft e dobishme me një numër të vogël kulmesh. Por kjo procedurë mund të zgjasë shumë nëse ka mjaft kulme.
Në këtë rast, është më e përshtatshme të merret në konsideratë një vijë niveli e formës f=a. Me një rritje monotonike të numrit a nga -∞ në +∞, drejtëzat f=a zhvendosen përgjatë vektorit normal. Nëse, me një lëvizje të tillë të vijës së nivelit, ekziston një pikë e caktuar X - pika e parë e përbashkët e rajonit të zgjidhjeve të realizueshme (polyedron ABCDE) dhe vijës së nivelit, atëherë f(X) është minimumi i f në grup. ABCDE. Nëse X është pika e fundit e kryqëzimit të vijës së nivelit dhe grupit ABCDE, atëherë f(X) është maksimumi në grupin e zgjidhjeve të realizueshme. Nëse, si a→-∞, drejtëza f=a pret bashkësinë e zgjidhjeve të realizueshme, atëherë min(f)= -∞. Nëse kjo ndodh si a→+∞, atëherë

Në shembullin tonë, drejtëza f=a pret zonën ABCDE në pikën C(4;1). Meqenëse kjo është pika e fundit e kryqëzimit, max(f)=f(C)=f(4;1)=19.
Metoda e thjeshtë
Problemet reale të programimit linear përmbajnë një numër shumë të madh kufizimesh dhe të panjohurash dhe kryhen në një kompjuter. Metoda Simplex është algoritmi më i përgjithshëm që përdoret për të zgjidhur probleme të tilla. Thelbi i metodës është që pas një numri të caktuar transformimesh të veçanta të Simpleksit, ZLP, e reduktuar në një formë të veçantë, zgjidhet. Për të demonstruar metodën simplex në veprim, le të zgjidhim problemin e mëposhtëm me komentet shoqëruese:

- Për të filluar zgjidhjen e problemit me metodën simplex, duhet ta sillni problemin në një formular të veçantë dhe të plotësoni tabelën simplex.
Sistemi (4) është një kufizim natyror dhe nuk përshtatet në tabelë. Ekuacionet (1), (2), (3) formojnë rajonin e zgjidhjeve të realizueshme. Shprehja (5) është funksioni objektiv. Kushtet e lira në sistemin e kufizimeve dhe rajoni i zgjidhjeve të pranueshme duhet të jenë jonegative.
Në këtë shembull, X3, X4, X5 janë të panjohurat themelore. Ato duhet të shprehen në terma të panjohura të lira dhe të zëvendësohen në funksionin objektiv.

Tani mund të filloni të plotësoni tabelën simplex:
| B. | X1 | X2 | X3 | X4 | X5 | C |
| X3 | 0 | -1 | 1 | 1 | 0 | 1 |
| X4 | 0 | 1 | -1 | 0 | 1 | 1 |
| X5 | 1 | 1 | 1 | 0 | 0 | 2 |
| f | 0 | -6 | 7 | 0 | 0 | 3 |
Kolona e parë e kësaj tabele tregon të panjohurat themelore, e fundit - vlerat e të panjohurave të lira, dhe pjesa tjetër - koeficientët e të panjohurave.
- Për të gjetur maksimumin e funksionit f, duke përdorur transformimet Gaussian, duhet të siguroheni që të gjithë koeficientët për të panjohurat në rreshtin e fundit të jenë jonegativë (për të gjetur minimumin, sigurohuni që të gjithë koeficientët të jenë më pak ose të barabartë në zero).
| B | X1 | X2 | X3 | X4 | X5 | C |
| X3 | -1 | 1 | 1 | 0 | 0 | 1 |
| X4 | 1 | -1 | 0 | 1 | 0 | 1 |
| X5 | 1 | 1 | 0 | 0 | 1 | 2 |
| f | -6 | 7 | 0 | 0 | 0 | 3 |
Për ta bërë këtë, zgjidhni kolonën me një koeficient negativ në rreshtin e fundit (kolona 3) dhe krijoni marrëdhënien e lirë term/koeficient (1/1; 2/1) për elementet pozitive të kësaj kolone. Nga këto raporte, zgjidhni më të voglin dhe shënoni vijën përkatëse.
Ne kemi zgjedhur elementin në qelizën (3;3). Tani, duke përdorur metodën Gaussian, ne rivendosim koeficientët e tjerë në këtë kolonë, kjo çon në një ndryshim në bazë dhe jemi një hap më afër zgjidhjes optimale.
| B | X1 | X2 | X3 | X4 | X5 | C |
| X3 | 0 | 0 | 1 | 1 | 0 | 2 |
| X1 | 1 | -1 | 0 | 1 | 0 | 1 |
| X5 | 0 | 2 | 0 | -1 | 1 | 1 |
| f | 0 | 1 | 0 | 6 | 0 | 9 |
Siç mund të shihet nga tabela, tani të gjithë koeficientët në rreshtin e fundit janë më të mëdhenj ose të barabartë me zero. Kjo do të thotë se ne kemi gjetur vlerën optimale. Të panjohurat e lira janë të barabarta me zero, vlera e të panjohurave bazë dhe maksimumi i funksionit f korrespondojnë me vlerat e të panjohurave të lira.
Një pabarazi është dy numra ose shprehje matematikore të lidhura me njërën nga shenjat: > (më e madhe se, në rastin e pabarazive strikte),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Pabarazia është lineare në të njëjtat kushte si ekuacioni: përmban variabla vetëm në shkallën e parë dhe nuk përmban produkte të ndryshoreve.
Zgjidhja e pabarazive lineare dhe sistemeve të pabarazive lineare është e lidhur pazgjidhshmërisht me kuptimin e tyre gjeometrik: zgjidhja e një pabarazie lineare është një gjysmë rrafsh i caktuar në të cilin i gjithë rrafshi ndahet me një vijë të drejtë, ekuacioni i së cilës përcakton pabarazinë lineare. . Ky gjysmërrafsh, dhe në rastin e një sistemi pabarazish lineare, pjesa e planit të kufizuar nga disa vija të drejta, duhet të gjendet në vizatim.
Shumë probleme ekonomike, në veçanti problemet e programimit linear, në të cilat kërkohet të gjendet maksimumi ose minimumi i një funksioni, reduktohen në zgjidhjen e sistemeve të pabarazive lineare me një numër të madh variablash.
Zgjidhja e sistemeve të pabarazive lineare me çdo numër të panjohurash
Së pari, le të shohim pabarazitë lineare në rrafsh. Konsideroni një pabarazi me dy ndryshore dhe:
![]() ,
,
ku janë koeficientët e variablave (disa numra), është termi i lirë (edhe një numër).
Një pabarazi me dy të panjohura, si një ekuacion, ka një numër të pafund zgjidhjesh. Zgjidhja e kësaj pabarazie është një çift numrash që plotësojnë këtë pabarazi. Gjeometrikisht, grupi i zgjidhjeve të një pabarazie përshkruhet si një gjysmë plan i kufizuar nga një vijë e drejtë.
![]() ,
,
të cilën do ta quajmë vijë kufitare.
Hapi 1. Ndërtoni një vijë që kufizon bashkësinë e zgjidhjeve me një pabarazi lineare
Për ta bërë këtë, ju duhet të dini çdo dy pika në këtë linjë. Le të gjejmë pikat e kryqëzimit me boshtet e koordinatave. Ordinata e kryqëzimit A e barabartë me zero (Figura 1). Vlerat numerike në akset në këtë figurë i referohen shembullit 1, të cilin do ta analizojmë menjëherë pas këtij ekskursioni teorik.

Abshisën e gjejmë duke zgjidhur ekuacionin e drejtëzës me ekuacionin e boshtit si sistem.
Le të gjejmë kryqëzimin me boshtin:

Duke zëvendësuar vlerën në ekuacionin e parë, marrim
Ku .
Kështu, gjetëm abshisën e pikës A .
Le të gjejmë koordinatat e pikës së kryqëzimit me boshtin.
Pikat e abshisave B e barabartë me zero. Le të zgjidhim ekuacionin e vijës kufitare me ekuacionin e boshtit të koordinatave:
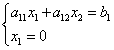
![]() ,
,
prandaj, koordinatat e pikës B: .
Hapi 2. Vizatoni një vijë të drejtë duke kufizuar grupin e zgjidhjeve në pabarazi. Njohja e pikave A Dhe B kryqëzimi i vijës kufitare me boshtet e koordinatave, mund ta vizatojmë këtë vijë. Një vijë e drejtë (përsëri Figura 1) e ndan të gjithë rrafshin në dy pjesë që shtrihen djathtas dhe majtas (sipër dhe poshtë) të kësaj vije të drejtë.
Hapi 3. Përcaktoni se cili gjysmërrafsh është zgjidhja e kësaj pabarazie. Për ta bërë këtë, ju duhet të zëvendësoni origjinën e koordinatave (0; 0) në këtë pabarazi. Nëse koordinatat e origjinës plotësojnë pabarazinë, atëherë zgjidhja e pabarazisë është gjysmërrafshi në të cilin ndodhet origjina. Nëse koordinatat nuk e plotësojnë pabarazinë, atëherë zgjidhja e pabarazisë është një gjysmëplan që nuk përmban origjinën. Gjysma e rrafshit të zgjidhjes së pabarazisë do të shënohet me goditje nga vija e drejtë në gjysmë rrafshi, si në figurën 1.
Nëse zgjidhim një sistem pabarazish lineare, atëherë çdo hap kryhet për secilën nga pabarazitë e sistemit.
Shembulli 1. Zgjidhja e pabarazisë
Zgjidhje. Le të vizatojmë një vijë të drejtë
Duke zëvendësuar një vijë të drejtë në ekuacion, marrim , dhe duke zëvendësuar , marrim . Prandaj, koordinatat e pikave të kryqëzimit me boshtet do të jenë A(3; 0) , B(0; 2) . Le të vizatojmë një vijë të drejtë nëpër këto pika (përsëri, Figura 1).

Le të zgjedhim një gjysmë plan zgjidhjesh të pabarazisë. Për ta bërë këtë, ne zëvendësojmë koordinatat e origjinës (0; 0) në pabarazinë:
marrim , d.m.th., koordinatat e origjinës e plotësojnë këtë pabarazi. Rrjedhimisht, zgjidhja e pabarazisë është gjysmë rrafshi që përmban origjinën e koordinatave, d.m.th., gjysmë rrafshi i majtë (aka më i ulët).
Nëse kjo pabarazi do të ishte e rreptë, domethënë do të kishte formën
atëherë pikat e vijës kufitare nuk do të ishin zgjidhje, pasi ato nuk plotësojnë pabarazinë.
Tani merrni parasysh një sistem pabarazish lineare me dy të panjohura:
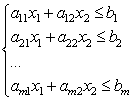
Secila nga pabarazitë e këtij sistemi në rrafsh përcakton një gjysmëplan. Një sistem pabarazish lineare quhet konsistent nëse ka të paktën një zgjidhje dhe jokonsistent nëse nuk ka zgjidhje. Një zgjidhje për një sistem pabarazish lineare është çdo çift numrash () që plotëson të gjitha pabarazitë e sistemit të caktuar.
Gjeometrikisht, zgjidhja e një sistemi të pabarazive lineare është grupi i pikave që plotësojnë të gjitha pabarazitë e sistemit, domethënë pjesa e përbashkët e gjysmërrafsheve që rezultojnë. Prandaj, gjeometrikisht, në rastin e përgjithshëm, zgjidhja mund të përshkruhet në formën e një shumëkëndëshi në një rast të veçantë, mund të jetë një vijë, një segment ose edhe një pikë. Nëse një sistem pabarazish lineare është i paqëndrueshëm, atëherë nuk ka asnjë pikë të vetme në rrafsh që plotëson të gjitha pabarazitë e sistemit.
Shembulli 2.
Zgjidhje. Pra, ne duhet të gjejmë një shumëkëndësh zgjidhjesh për këtë sistem pabarazish. Le të ndërtojmë një vijë kufitare për pabarazinë e parë, pra një vijë, dhe një vijë kufitare për pabarazinë e dytë, domethënë një vijë.
Ne e bëjmë këtë hap pas hapi, siç u tregua në referencën teorike dhe në shembullin 1, veçanërisht pasi në shembullin 1 ndërtuam një vijë kufitare për pabarazinë, e cila është e para në këtë sistem.

Gjysmë-rrafshët e zgjidhjeve që korrespondojnë me pabarazitë e këtij sistemi janë të hijezuara nga brenda në Figurën 2. Pjesa e përbashkët e gjysmëplaneve të zgjidhjes është një kënd i hapur ABC. Kjo do të thotë se bashkësia e pikave në rrafsh që përbëjnë një kënd të hapur ABC, është një zgjidhje për të dyja pabarazitë e para dhe të dyta të sistemit, domethënë është një zgjidhje e një sistemi me dy pabarazi lineare. Me fjalë të tjera, koordinatat e çdo pike nga ky grup plotësojnë të dyja pabarazitë e sistemit.
Shembulli 3. Zgjidh një sistem pabarazish lineare
Zgjidhje. Le të ndërtojmë vija kufitare që korrespondojnë me pabarazitë e sistemit. Këtë e bëjmë duke ndjekur hapat e dhëna në ndihmën teorike për çdo pabarazi. Tani përcaktojmë gjysmëplanet e zgjidhjeve për secilën pabarazi (Figura 3).

Gjysmë-rrafshët e zgjidhjeve që korrespondojnë me pabarazitë e një sistemi të caktuar janë të hijezuara nga brenda. Kryqëzimi i gjysmëplaneve të zgjidhjeve është paraqitur, siç tregohet në figurë, në formën e një katërkëndëshi ABCE. Ne zbuluam se shumëkëndëshi i zgjidhjeve të një sistemi të pabarazive lineare me dy ndryshore është një katërkëndësh ABCE .
Gjithçka e përshkruar më sipër për sistemet e pabarazive lineare me dy të panjohura vlen edhe për sistemet e pabarazive me çdo numër të panjohurash, me ndryshimin e vetëm që zgjidhja e pabarazisë me n të panjohurat do të jenë tërësia n numrat () që plotësojnë të gjitha pabarazitë, dhe në vend të vijës kufitare do të ketë një hiperplan kufitar n-hapësirë dimensionale. Zgjidhja do të jetë një poliedron i zgjidhjes (i thjeshtë) i kufizuar nga hiperplane.
Artikulli i mëparshëm: Sa është shpejtësia e dritës Artikulli vijues: Karakteristikat e elementit të karbonit dhe vetitë kimike
