Si të gjeni këndin midis vijave të metodës së koordinatave. Këndi ndërmjet dy rrafsheve të kryqëzuara - përkufizimi, shembuj të gjetjes

Problemi 1.6. Kubi i dhënë. M, N, P - pikat e mesit të skajeve, përkatësisht, AB, BC. Gjeni këndin ndërmjet planeve (MNP) dhe

a) Prezantojmë një sistem koordinativ kartezian drejtkëndor siç tregohet në figurën 17. Gjatësia e skajit të kubit mund të zgjidhet në mënyrë arbitrare, pasi këndi midis rrafsheve nuk ndryshon nën homoteti. Është e përshtatshme, për shembull, të marrësh gjatësinë e skajit të një kubi të barabartë me 2.

Në lidhje me sistemin e zgjedhur të koordinatave, gjejmë koordinatat e pikave dhe vektorëve:

b) Le të jetë një vektor normal i rrafshit.

Në këtë rast, kushtet

Në mënyrë të ngjashme, nëse është vektori normal i rrafshit, atëherë

c) Nëse atëherë

Përgjigje:

Problemi 1.7. Në bazën e një piramide të rregullt trekëndore SABC shtrihet një e rregullt me brinjë të barabartë me 2. Buza SA është pingul me rrafshin e bazës dhe SA = 1. Pikat P, Q janë përkatësisht mesi i skajeve SB, CB. Rrafshi është paralel me drejtëzat SC dhe AB, dhe rrafshi është paralel me drejtëzat AQ dhe CP. Përcaktoni këndin ndërmjet rrafsheve dhe.

a) Zgjedhim një sistem koordinativ kartezian drejtkëndor siç tregohet në figurën 18. Në sistemin koordinativ të zgjedhur kemi:

b) është vektori normal i rrafshit paralel me drejtëzat SC dhe AB. atëherë plotësohen kushtet e mëposhtme:

c) Shënoni me një rrafsh që është paralel me drejtëzat AQ dhe CP, dhe me - vektorin e tij normal. Në këtë rast, marrim një sistem të formës

Qëllimet:

• të zhvillojë aftësinë për të shqyrtuar qasje të ndryshme për zgjidhjen e problemeve dhe të analizojë "efektin" e aplikimit të këtyre metodave të zgjidhjes;
• të zhvillojë aftësinë e studentit për të zgjedhur një metodë për zgjidhjen e një problemi në përputhje me preferencat e tyre matematikore, bazuar në njohuri më solide dhe aftësi të sigurta;
• të zhvillojë aftësinë për të hartuar një plan të fazave të njëpasnjëshme për të arritur rezultatin;
• të zhvillojë aftësinë për të justifikuar të gjitha hapat dhe llogaritjet e ndërmarra;
• të përsërisë dhe të konsolidojë tema dhe çështje të ndryshme të stereometrisë dhe planimetrisë, struktura tipike stereometrike që lidhen me zgjidhjen e problemeve aktuale;
• zhvillojnë të menduarit hapësinor.

• analiza e metodave të ndryshme për zgjidhjen e problemës: metoda koordinative-vektoriale, zbatimi i teoremës së kosinusit, zbatimi i teoremës së tre pingulave;
• duke krahasuar avantazhet dhe disavantazhet e secilës metodë;
• përsëritja e vetive të kubit, prizmit trekëndor, gjashtëkëndëshit të rregullt;
• përgatitja për dhënien e provimit;
• zhvillimi i pavarësisë në vendimmarrje.

Skica e mësimit

Në kubikë ABCDA 1 B 1 C 1 D 1 me buzë 1 pikë O - qendra e fytyrës ABCD.

a) këndi ndërmjet vijave A 1 D dhe BO;

b) largësia nga pika B deri në mes të prerjes A 1 D.

Pika e vendimit a).

Le ta vendosim kubin tonë në një sistem koordinativ drejtkëndor siç tregohet në figurë, kulmet A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0).

Vektorët e drejtimit të vijave A 1 D dhe B1O:

(0; 1; -1) dhe (½; ½; -1);

këndi i dëshiruar φ ndërmjet tyre gjendet me formulën:

cos∠φ = ,
prej nga ∠φ = 30°.

2 mënyra. Ne përdorim teoremën e kosinusit.

1) Vizatoni një vijë të drejtë Në 1 C paralel me një vijë të drejtë A 1 D. Këndi CB1O do të jetë e dëshiruar.

2) Nga një trekëndësh kënddrejtë BB 1 O sipas teoremës së Pitagorës:

3) Sipas ligjit të kosinusit nga një trekëndësh CB1O llogarit këndin CB1O:

cos CB 1 O = , këndi i dëshiruar është 30°.

Komentoni. Kur zgjidhet problema në mënyrën e dytë, shihet se, sipas teoremës mbi tre pingulet COB 1 = 90°, pra nga drejtkëndëshi ∆ CB1Oështë gjithashtu e lehtë të llogaritet kosinusi i këndit të dëshiruar.

Pika e vendimit b).

1 mënyrë. Le të përdorim formulën për distancën midis dy pikave

Lëreni pikën E- mes A 1 D, pastaj koordinatat E (1; 1/2; ½), B (0; 0; 0).

B.E.= .

2 mënyra. Sipas teoremës së Pitagorës

Nga drejtkëndëshi ∆ BAE me direkt BAE Gjej BE = .

Në një prizëm të rregullt trekëndor ABCA 1 B 1 C 1 të gjitha skajet janë të barabarta a. Gjeni këndin midis vijave AB dhe A 1 C.

1 mënyrë. Metoda e vektorit të koordinatave

Koordinatat e kulmeve të prizmit në një sistem drejtkëndor kur ndodhet prizmi, si në figurë: A (0; 0; 0), B (a; ; 0), A 1 (0; 0; a), C (0; a; 0).

Vektorët e drejtimit të vijave A 1 C dhe AB:

(0; a; -a) dhe (a; ; 0} ;

cos φ = ;

2 mënyra. Ne përdorim ligjin e kosinusit

Ne konsiderojmë ∆ A 1 B 1 C, ku A 1 B 1 || AB. Ne kemi

cos φ = .

(Nga koleksioni i Provimit të Unifikuar të Shtetit-2012. Matematika: opsionet tipike të provimit, redaktuar nga A.L. Semenov, I.V. Yashchenko)

Në një prizëm të rregullt gjashtëkëndor ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, të gjitha skajet e së cilës janë të barabarta me 1, gjeni distancën nga pika E drejt drejt B 1 C 1.

1 mënyrë. Metoda e vektorit të koordinatave

1) Vendosni prizmin në një sistem koordinativ drejtkëndor, duke vendosur boshtet e koordinatave siç tregohet në figurë. SS 1, JP dhe CE janë pingul në çift, kështu që boshtet e koordinatave mund të drejtohen përgjatë tyre. Ne marrim koordinatat:

C 1 (0; 0; 1), E (; 0; 0), B 1 (0; 1; 1).

2) Gjeni koordinatat e vektorëve të drejtimit për vijat Nga 1 në 1 dhe C 1 E:

(0;1;0), (;0;-1).

3) Gjeni kosinusin e këndit ndërmjet Nga 1 në 1 dhe C 1 E, duke përdorur produktin skalar të vektorëve dhe :

cos β = = 0 => β = 90° => C 1 E është distanca e kërkuar.

4)C 1 E \u003d \u003d 2.

Përfundim: njohja e qasjeve të ndryshme për zgjidhjen e problemeve stereometrike ju lejon të zgjidhni metodën e preferuar për çdo student, d.m.th. ai për të cilin studenti ka besim, ndihmon në shmangien e gabimeve, çon në një zgjidhje të suksesshme të problemit dhe marrjen e një rezultati të mirë në provim. Metoda e koordinatave ka një avantazh ndaj metodave të tjera në atë që kërkon më pak konsiderata dhe vizion stereometrik dhe bazohet në përdorimin e formulave që kanë shumë analogji planimetrike dhe algjebrike që janë më të njohura për studentët.

Forma e orës së mësimit është një ndërthurje e shpjegimit të mësuesit me punën kolektive ballore të nxënësve.

Polyedronet në shqyrtim shfaqen në ekran duke përdorur një videoprojektor, i cili bën të mundur krahasimin e zgjidhjeve të ndryshme.

Detyrë shtëpie: zgjidhni problemin 3 në një mënyrë tjetër, për shembull, duke përdorur teoremën e tre pingulave .

Letërsia

1. Ershova A.P., Goloborodko V.V. Punë e pavarur dhe kontrolluese për gjeometrinë për klasën 11. - M .: ILEKSA, - 2010. - 208 f.

2. Gjeometria, 10-11: tekst shkollor për institucionet arsimore: nivelet bazë dhe të profilit / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev dhe të tjerët - M .: Arsimi, 2007. - 256 f.

3. PËRDORIMI-2012. Matematika: opsionet tipike të provimit: 10 opsione / ed. A.L. Semenova, I.V. Yashchenko. - M.: Arsimi kombëtar, 2011. - 112 f. - (USE-2012. FIPI - shkolla).

Artikulli flet për gjetjen e këndit midis avionëve. Pasi të sjellim përkufizimin, ne do të vendosim një ilustrim grafik, do të shqyrtojmë një metodë të detajuar për gjetjen e koordinatave me metodën. Ne marrim një formulë për rrafshet e kryqëzimit, e cila përfshin koordinatat e vektorëve normalë.

Yandex.RTB R-A-339285-1

Materiali do të përdorë të dhëna dhe koncepte që janë studiuar më parë në artikujt rreth aeroplanit dhe linjës në hapësirë. Për të filluar, është e nevojshme të kalojmë në arsyetimin që lejon që dikush të ketë një qasje të caktuar për përcaktimin e këndit midis dy planeve kryqëzuese.

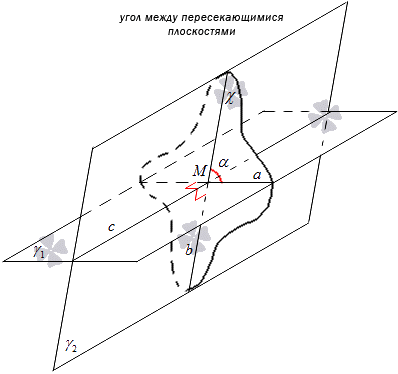
Janë dhënë dy plane kryqëzuese γ 1 dhe γ 2. Kryqëzimi i tyre do të marrë emërtimin c. Ndërtimi i rrafshit χ është i lidhur me kryqëzimin e këtyre rrafsheve. Rrafshi χ kalon në pikën M si drejtëz c. Planet γ 1 dhe γ 2 do të priten duke përdorur rrafshin χ. Ne pranojmë emërtimet e drejtëzës që kryqëzon γ 1 dhe χ për drejtëzën a, dhe që pret γ 2 dhe χ për drejtëzën b. Marrim se prerja e drejtëzave a dhe b jep pikën M.

Vendndodhja e pikës M nuk ndikon në këndin ndërmjet drejtëzave të kryqëzuara a dhe b, dhe pika M ndodhet në drejtëzën c nëpër të cilën kalon rrafshi χ.

Është e nevojshme të ndërtohet një rrafsh χ 1 pingul me drejtëzën c dhe i ndryshëm nga rrafshi χ . Prerja e rrafsheve γ 1 dhe γ 2 me ndihmën e χ 1 do të marrë emërtimin e drejtëzave a 1 dhe b 1 .

Mund të shihet se kur ndërtohen χ dhe χ 1, drejtëzat a dhe b janë pingul me drejtëzën c, pastaj a 1, b 1 janë pingul me drejtëzën c. Gjetja e drejtëzave a dhe a 1 në rrafshin γ 1 me pingul në drejtëzën c, atëherë ato mund të konsiderohen paralele. Në të njëjtën mënyrë, vendndodhja e b dhe b 1 në rrafshin γ 2 me pingulitetin e drejtëzës c tregon paralelizmin e tyre. Kjo do të thotë se është e nevojshme të bëhet një transferim paralel i rrafshit χ 1 në χ, ku marrim dy drejtëza që përputhen a dhe a 1 , b dhe b 1 . Marrim se këndi ndërmjet drejtëzave a dhe b 1 të prerjes është i barabartë me këndin e drejtëzave të prera a dhe b.

Konsideroni figurën më poshtë.

Ky gjykim vërtetohet me faktin se midis drejtëzave të kryqëzuara a dhe b ekziston një kënd që nuk varet nga vendndodhja e pikës M, domethënë nga pika e kryqëzimit. Këto vija ndodhen në rrafshet γ 1 dhe γ 2 . Në fakt, këndi që rezulton mund të mendohet si këndi ndërmjet dy rrafsheve të kryqëzuara.

Le të kalojmë në përcaktimin e këndit midis planeve ekzistuese kryqëzuese γ 1 dhe γ 2 .

Përkufizimi 1

Këndi ndërmjet dy rrafsheve të kryqëzuara γ 1 dhe γ 2 quajmë këndin e formuar nga prerja e drejtëzave a dhe b, ku rrafshet γ 1 dhe γ 2 priten me rrafshin χ pingul me drejtëzën c.

Konsideroni figurën më poshtë.

Përkufizimi mund të paraqitet në një formë tjetër. Në kryqëzimin e rrafsheve γ 1 dhe γ 2, ku c është drejtëza në të cilën ata kryqëzohen, shënoni pikën M, përmes së cilës vizatoni drejtëzat a dhe b, pingul me drejtëzën c dhe që shtrihen në rrafshet γ 1 dhe γ. 2, atëherë këndi ndërmjet drejtëzave a dhe b do të jetë këndi ndërmjet rrafsheve. Në praktikë, kjo është e zbatueshme për ndërtimin e një këndi midis planeve.

Gjatë kryqëzimit formohet një kënd me vlerë më të vogël se 90 gradë, domethënë masa e shkallës së këndit është e vlefshme në një interval të këtij lloji (0, 90 ] . Në të njëjtën kohë, këto plane quhen pingul nëse në kryqëzim formohet një kënd i drejtë.Këndi ndërmjet rrafsheve paralele konsiderohet i barabartë me zero.

Mënyra e zakonshme për të gjetur këndin midis planeve të kryqëzuara është të kryhen ndërtime shtesë. Kjo ndihmon për ta përcaktuar me saktësi, dhe kjo mund të bëhet duke përdorur shenjat e barazisë ose ngjashmërisë së trekëndëshit, sinuseve, kosinuseve të këndit.

Konsideroni zgjidhjen e problemeve duke përdorur një shembull nga problemet e Provimit të Unifikuar të Shtetit të bllokut C 2.

Shembulli 1

Jepet një paralelipiped drejtkëndor A B C D A 1 B 1 C 1 D 1, ku ana A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, pika E ndan anën A A 1 në një raport 4: 3. Gjeni këndin ndërmjet rrafsheve A B C dhe B E D 1 .

Zgjidhje

Për qartësi, duhet të bëni një vizatim. Ne e kuptojmë atë

Një paraqitje vizuale është e nevojshme për ta bërë më të përshtatshëm punën me këndin midis avionëve.

Bëjmë përcaktimin e një drejtëze përgjatë së cilës kryqëzohen rrafshet A B C dhe B E D 1. Pika B është një pikë e zakonshme. Duhet gjetur një pikë tjetër e përbashkët kryqëzimi. Konsideroni drejtëzat D A dhe D 1 E , të cilat ndodhen në të njëjtin rrafsh A D D 1 . Vendndodhja e tyre nuk tregon paralelizëm, që do të thotë se ata kanë një pikë të përbashkët kryqëzimi.

Megjithatë, linja D A ndodhet në rrafshin A B C, dhe D 1 E në B E D 1 . Prandaj marrim se linjat D A dhe D 1 E kanë një pikë të përbashkët kryqëzimi, e cila është gjithashtu e zakonshme për rrafshet A B C dhe B E D 1 . Tregon pikën e kryqëzimit të vijave D A dhe D 1 E shkronja F. Nga këtu marrim se B F është një vijë e drejtë përgjatë së cilës kryqëzohen rrafshet A B C dhe B E D 1.

Konsideroni figurën më poshtë.

Për të marrë një përgjigje, është e nevojshme të ndërtohen drejtëza të vendosura në rrafshet A B C dhe B E D 1 me kalimin nëpër një pikë të vendosur në drejtëzën B F dhe pingul me të. Pastaj këndi që rezulton midis këtyre vijave konsiderohet këndi i dëshiruar midis planeve A B C dhe B E D 1.

Nga kjo mund të shihet se pika A është projeksioni i pikës E në rrafshin A B C. Është e nevojshme të vizatohet një vijë që pret drejtëzën B F në një kënd të drejtë në pikën M. Mund të shihet se drejtëza A M është projeksioni i drejtëzës E M në rrafshin A B C, bazuar në teoremën rreth atyre pingulave A M ⊥ B F . Konsideroni figurën më poshtë.

∠ A M E është këndi i dëshiruar i formuar nga rrafshet A B C dhe B E D 1 . Nga trekëndëshi rezultues A E M mund të gjejmë sinusin, kosinusin ose tangjentën e këndit, pas së cilës vetë këndi, vetëm me dy brinjët e tij të njohura. Me kusht, ne kemi që gjatësia e A E të gjendet në këtë mënyrë: rreshti A A 1 ndahet me pikën E në një raport 4: 3, që do të thotë se gjatësia totale e rreshtit është 7 pjesë, pastaj A E \u003d 4 pjesë. Ne gjejmë A.M.

Është e nevojshme të merret parasysh një trekëndësh kënddrejtë A B F. Ne kemi një kënd të drejtë A me lartësi A M. Nga kushti A B \u003d 2, atëherë mund të gjejmë gjatësinë A F nga ngjashmëria e trekëndëshave D D 1 F dhe A E F. Marrim se A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Është e nevojshme të gjendet gjatësia e brinjës B F nga trekëndëshi A B F duke përdorur teoremën e Pitagorës. Marrim se B F   = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Gjatësia e brinjës A M gjendet përmes sipërfaqes së trekëndëshit A B F. Kemi që zona mund të jetë e barabartë si me S A B C = 1 2 · A B · A F , dhe me S A B C = 1 2 · B F · A M .

Marrim se A M = A B A F B F = 2 4 2 5 = 4 5 5

Atëherë mund të gjejmë vlerën e tangjentes së këndit të trekëndëshit A E M. Marrim:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Këndi i dëshiruar i marrë nga kryqëzimi i planeve A B C dhe B E D 1 është i barabartë me një r c t g 5, atëherë, kur thjeshtohet, marrim një r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Përgjigje: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Janë dhënë disa raste të gjetjes së këndit ndërmjet drejtëzave të kryqëzuara duke përdorur planin koordinativ O x y z dhe metodën e koordinatave. Le të shqyrtojmë më në detaje.

Nëse jepet një problem ku është e nevojshme të gjendet këndi ndërmjet rrafsheve kryqëzuese γ 1 dhe γ 2, këndin e dëshiruar e shënojmë me α.

Atëherë sistemi i koordinatave të dhëna tregon se kemi koordinatat e vektorëve normalë të rrafsheve të kryqëzuara γ 1 dhe γ 2 . Pastaj shënojmë se n 1 → = n 1 x , n 1 y , n 1 z është një vektor normal i rrafshit γ 1 , dhe n 2 → = (n 2 x , n 2 y , n 2 z) - për rrafshi γ 2 . Konsideroni një gjetje të detajuar të këndit të vendosur midis këtyre planeve sipas koordinatave të vektorëve.

Është e nevojshme të caktohet vija e drejtë përgjatë së cilës aeroplanët γ 1 dhe γ 2 kryqëzohen me shkronjën c. Në drejtëzën me kemi një pikë M, përmes së cilës vizatojmë një rrafsh χ, pingul me c. Rrafshi χ përgjatë drejtëzave a dhe b pret rrafshet γ 1 dhe γ 2 në pikën M . Nga përkufizimi del se këndi ndërmjet rrafsheve të kryqëzuara γ 1 dhe γ 2 është i barabartë me këndin e drejtëzave prerëse a dhe b që u përkasin përkatësisht këtyre rrafsheve.

Në rrafshin χ, i lëmë mënjanë vektorët normalë nga pika M dhe i shënojmë n 1 → dhe n 2 →. Vektori n 1 → ndodhet në një drejtëz pingul me drejtëzën a, dhe vektori n 2 → në një drejtëz pingul me drejtëzën b. Nga këtu marrim se rrafshi i dhënë χ ka një vektor normal të drejtëzës a të barabartë me n 1 → dhe për drejtëzën b të barabartë me n 2 → . Konsideroni figurën më poshtë.

Nga këtu marrim një formulë me të cilën mund të llogarisim sinusin e këndit të drejtëzave të kryqëzuara duke përdorur koordinatat e vektorëve. Ne zbuluam se kosinusi i këndit midis drejtëzave a dhe b është i njëjtë me kosinusin midis planeve kryqëzuese γ 1 dhe γ 2 rrjedh nga formula cos α = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , ku kemi se n 1 → = (n 1 x , n 1 y , n 1 z) dhe n 2 → = (n 2 x , n 2 y , n 2 z) janë koordinatat e vektorëve të planeve të paraqitura.

Këndi midis vijave të kryqëzuara llogaritet duke përdorur formulën

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Shembulli 2

Me kusht jepet një paralelipiped А В С D A 1 B 1 C 1 D 1 , ku A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, dhe pika E ndan anën A A 1 4: 3. Gjeni këndin ndërmjet rrafsheve A B C dhe B E D 1 .

Zgjidhje

Mund të shihet nga kushti që anët e tij të jenë pingule në çift. Kjo do të thotë se është e nevojshme të futet një sistem koordinativ O x y z me kulm në pikën C dhe boshtet koordinative O x, O y, O z. Është e nevojshme të vendosni drejtimin në anët e duhura. Konsideroni figurën më poshtë.

Planet e kryqëzimit A B C dhe B E D 1 formoni një kënd, i cili mund të gjendet me formulën 2 x 2 + n 2 y 2 + n 2 z 2 , ku n 1 → = (n 1 x , n 1 y , n 1 z) dhe n 2 → = (n 2 x , n 2 y , n 2 z ) janë vektorë normalë të këtyre planeve. Është e nevojshme të përcaktohen koordinatat. Nga figura shohim se boshti i koordinatave O x y përkon në rrafshin A B C, që do të thotë se koordinatat e vektorit normal k → janë të barabarta me vlerën n 1 → = k → = (0, 0, 1) .

Vektori normal i planit B E D 1 është prodhimi vektorial B E → dhe B D 1 → , ku koordinatat e tyre gjenden me koordinatat e pikave ekstreme B, E, D 1 , të cilat përcaktohen në bazë të gjendjes së problemit.

Marrim se B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Sepse A E E A 1 = 4 3 , nga koordinatat e pikave A 2 , 3 , 0 , A 1 2 , 3 , 7 gjejmë E 2 , 3 , 4 . Marrim se B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

Është e nevojshme të zëvendësohen koordinatat e gjetura në formulën për llogaritjen e këndit përmes kosinusit të harkut. marrim

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Metoda e koordinatave jep një rezultat të ngjashëm.

Përgjigje: a r c cos 6 6 .

Problemi përfundimtar merret parasysh për të gjetur këndin midis planeve të kryqëzuara me ekuacionet e disponueshme të njohura të planeve.

Shembulli 3

Llogaritni sinusin, kosinusin e këndit dhe vlerën e këndit të formuar nga dy drejtëza të kryqëzuara, të cilat përcaktohen në sistemin koordinativ O x y z dhe jepen nga ekuacionet 2 x - 4 y + z + 1 = 0 dhe 3 y - z - 1 = 0 .

Zgjidhje

Gjatë studimit të temës së ekuacionit të përgjithshëm të drejtëzës së formës A x + B y + C z + D = 0, u zbulua se A, B, C janë koeficientë të barabartë me koordinatat e vektorit normal. Prandaj, n 1 → = 2 , - 4 , 1 dhe n 2 → = 0 , 3 , - 1 janë vektorë normalë të linjave të dhëna.

Është e nevojshme të zëvendësohen koordinatat e vektorëve normalë të planeve në formulën për llogaritjen e këndit të dëshiruar të planeve të kryqëzimit. Pastaj e marrim atë

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Prandaj kemi që kosinusi i këndit merr formën cos α = 13 210 . Atëherë këndi i vijave të kryqëzuara nuk është i mpirë. Duke zëvendësuar në identitetin trigonometrik, marrim se vlera e sinusit të këndit është e barabartë me shprehjen. Ne e llogarisim dhe e marrim atë

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Përgjigje: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .

Nëse vëreni një gabim në tekst, ju lutemi theksoni atë dhe shtypni Ctrl+Enter

Detyra 1. Baza e një prizmi të drejtë katërkëndor ABCD 1 B 1 C 1 D 1 është një drejtkëndësh ABCD, në të cilin AB \u003d 5, AD \u003d 11. Gjeni tangjentën e këndit midis rrafshit të bazës së prizmit dhe rrafshi që kalon nga mesi i skajit AD pingul me drejtëzën BD 1, nëse distanca ndërmjet drejtëzave AC dhe B 1 D 1 është 12. Zgjidhje. Ne prezantojmë një sistem koordinativ. В(0;0;0), А(5;0;0), С(0;11;0), D 1 (5;11;12) Koordinatat e normales në rrafshin e seksionit: Koordinatat e normales në rrafshi bazë: – këndi akut, pastaj D A B C D1D1 A1A1 B1B1 C1C1 x y z N Këndi ndërmjet rrafsheve Përgjigje: 0.5. Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 2. Në bazën e piramidës trekëndore SABC shtrihet një trekëndësh kënddrejtë ABC. Këndi A është i drejtë. AC \u003d 8, BC \u003d 219. Lartësia e piramidës SA është 6. Një pikë M merret në skajin AC në mënyrë që AM \u003d 2. Një plan α tërhiqet përmes pikës M, kulmit B dhe pika N - mesi i skajit SC. Gjeni këndin dihedral të formuar nga rrafshi α dhe rrafshi i bazës së piramidës. A S x B C M N y z Zgjidhje. Ne prezantojmë një sistem koordinativ. Pastaj A (0;0;0), C (0;8;0), M (0;2;0), N (0;4;3), S (0;0;6), Normale në aeroplan ( ABC) vektor Normal në rrafsh (BMN) Këndi ndërmjet planeve Përgjigje: 60°. Ekuacioni i aeroplanit (ВМN): N.G. Nenasheva mësues matematike GBOU shkolla e mesme 985

Problemi 3. Baza e një piramide katërkëndore PABCD është një katror me brinjë të barabartë me 6, buza anësore PD është pingul me rrafshin e bazës dhe është e barabartë me 6. Gjeni këndin ndërmjet rrafsheve (BDP) dhe (BCP). Zgjidhje. 1. Vizatoni DF-në mesatare të një trekëndëshi dykëndësh CDP (BC = PD = 6) Pra DF PC. Dhe nga fakti që BC (CDP), rrjedh se DF BC do të thotë DF (PCB) A D C B P F 2. Meqenëse AC DB dhe AC DP, atëherë AC (BDP) 3. Kështu, këndi midis rrafsheve (BDP) dhe (BCP) ) gjendet nga kushti: Këndi ndërmjet rrafsheve Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 3. Baza e një piramide katërkëndore PABCD është një katror me brinjë të barabartë me 6, buza anësore PD është pingul me rrafshin e bazës dhe është e barabartë me 6. Gjeni këndin ndërmjet rrafsheve (BDP) dhe (BCP). Zgjidhje.4. Le të zgjedhim një sistem koordinativ. Koordinatat e pikave: 5. Atëherë vektorët do të kenë këto koordinata: 6. Duke llogaritur vlerat, gjejmë:, pastaj A D C B P F z x y Këndi ndërmjet rrafsheve Përgjigje: Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 4. Në kubin njësi ABCDA 1 B 1 C 1 D 1, gjeni këndin midis rrafsheve (AD 1 E) dhe (D 1 FC), ku pikat E dhe F janë mesi i skajeve A 1 B 1 dhe B 1 C 1, përkatësisht. Zgjidhje: 1. Të prezantojmë një sistem koordinativ drejtkëndor dhe të përcaktojmë koordinatat e pikave: 2. Të hartojmë ekuacionin e rrafshit (AD 1 E): 3. Të hartojmë ekuacionin e rrafshit (D 1 FC): - vektorin normal. i aeroplanit (AD 1 E). - vektori normal i rrafshit (D 1 FС). Këndi ndërmjet rrafsheve x y z Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 4. Në kubin njësi ABCDA 1 B 1 C 1 D 1, gjeni këndin midis rrafsheve (AD 1 E) dhe (D 1 FC), ku pikat E dhe F janë mesi i skajeve A 1 B 1 dhe B 1 C 1, përkatësisht. Zgjidhje: 4. Gjeni kosinusin e këndit ndërmjet rrafsheve duke përdorur formulën Përgjigje: Këndi ndërmjet rrafsheve x y z Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 5. Segmenti që lidh qendrën e bazës së një piramide të rregullt trekëndore me mesin e buzës anësore është i barabartë me faqen e bazës. Gjeni këndin midis faqeve anësore fqinje të piramidës. Zgjidhje: x y z 1. Le të prezantojmë një sistem koordinativ drejtkëndor dhe të përcaktojmë koordinatat e pikave A, B, C: K Le të jetë faqja e bazës 1. Për të përcaktuar, konsideroni faqet SAC dhe SBC 2. Gjeni koordinatat e pikës S: E Këndi ndërmjet rrafsheve Nenasheva N.G . mësues matematike GBOU shkolla e mesme 985

Problemi 5. Segmenti që lidh qendrën e bazës së një piramide të rregullt trekëndore me mesin e buzës anësore është i barabartë me faqen e bazës. Gjeni këndin midis faqeve anësore fqinje të piramidës. Zgjidhje: x y z K E SO gjejmë nga OSB: Këndi ndërmjet rrafsheve Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 5. Segmenti që lidh qendrën e bazës së një piramide të rregullt trekëndore me mesin e buzës anësore është i barabartë me faqen e bazës. Gjeni këndin midis faqeve anësore fqinje të piramidës. Zgjidhje: x y z K E 3. Ekuacioni i rrafshit (SAC): - vektori normal i rrafshit (SAC). 4. Ekuacioni i rrafshit (SBC): - vektori normal i rrafshit (SBC). Këndi ndërmjet avionëve Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Problemi 5. Segmenti që lidh qendrën e bazës së një piramide të rregullt trekëndore me mesin e buzës anësore është i barabartë me faqen e bazës. Gjeni këndin midis faqeve anësore fqinje të piramidës. Zgjidhje: x y z K E 5. Gjeni kosinusin e këndit ndërmjet rrafsheve sipas formulës Përgjigje: Këndi ndërmjet rrafsheve Nenasheva N.G. mësues matematike GBOU shkolla e mesme 985

Përdorimi i metodës së koordinatave gjatë llogaritjes së një këndi

mes avionëve

Metoda më e përgjithshme për gjetjen e një këndimidis planeve - metoda e koordinatave (nganjëherë - me përfshirjen e vektorëve). Mund të përdoret kur të gjitha të tjerat janë provuar. Por ka situata në të cilat ka kuptim të zbatohet menjëherë metoda e koordinatave, domethënë, kur sistemi i koordinatave lidhet natyrshëm me poliedrin e specifikuar në deklaratën e problemit, d.m.th. duken qartë tre vija pingule në çift, mbi të cilat mund të vendosen boshtet e koordinatave. Të tilla poliedra janë një paralelipiped drejtkëndor dhe një piramidë e rregullt katërkëndore. Në rastin e parë, sistemi i koordinatave mund të vendoset nga skajet që dalin nga një kulm (Fig. 1), në të dytën - nga lartësia dhe diagonalet e bazës (Fig. 2)

Zbatimi i metodës së koordinatave është si më poshtë.

Një sistem koordinativ drejtkëndor është futur në hapësirë. Është e dëshirueshme ta prezantoni atë në një mënyrë "natyrore" - "bashkëngjitni" me një treshe linjash pingule në çift që kanë një pikë të përbashkët.

Për secilin prej rrafsheve, këndi ndërmjet të cilit kërkohet, hartohet një ekuacion. Mënyra më e lehtë për të shkruar një ekuacion të tillë është të njohësh koordinatat e tre pikave në rrafsh që nuk shtrihen në një vijë të drejtë.

Ekuacioni i rrafshët në formë të përgjithshme ka formën Ax + By + Cz + D = 0.

Koeficientët A, B, C në këtë ekuacion janë koordinatat e vektorit normal të rrafshit (vektori pingul me rrafshin). Më pas përcaktojmë gjatësitë dhe produktin skalar të vektorëve normalë ndaj planeve, këndi ndërmjet të cilit kërkohet. Nëse koordinatat e këtyre vektorëve(A 1, B 1; C 1) dhe (A 2; B 2; C 2 ), pastaj këndi i dëshiruarllogaritur me formulë

Komentoni. Duhet mbajtur mend se këndi midis vektorëve (në krahasim me këndin midis planeve) mund të jetë i mpirë, dhe për të shmangur pasigurinë e mundshme, numëruesi i anës së djathtë të formulës është moduli.

Zgjidheni problemin e mëposhtëm duke përdorur metodën e koordinatave.

Detyra 1. Është dhënë një kub ABCDA 1 B 1 C 1 D 1. Pika K është mesi i skajit AD, pika L është mesi i skajit CD. Cili është këndi ndërmjet rrafsheve A 1 KL dhe A 1 pas Krishtit?

Zgjidhje . Le të jetë origjina e sistemit të koordinatave në pikën POR, dhe boshtet e koordinatave shkojnë përgjatë rrezeve AD, AB, AA 1 (Fig. 3). Ne marrim skajin e kubit të barabartë me 2 (është i përshtatshëm për ta ndarë në gjysmë). Pastaj koordinatat e pikave A 1, K, L janë: A 1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).

Oriz. 3

Shkruajmë ekuacionin e rrafshit Një 1 KL në përgjithësi. Pastaj ne zëvendësojmë koordinatat e pikave të zgjedhura të këtij plani në të. Ne marrim një sistem prej tre ekuacionesh me katër të panjohura:

Shprehim koeficientët A, B, C deri në D dhe vijnë në ekuacion

Duke i ndarë të dyja pjesët në D (pse D= 0?) dhe më pas duke shumëzuar me -2, marrim ekuacionin e rrafshit A 1 KL: 2x - 2 y + z - 2 = 0. Atëherë vektori normal në këtë rrafsh ka koordinata (2: -2; 1) . Ekuacioni i planit Një 1 pas Krishtit është: y=0, dhe koordinatat e vektorit normal për të, për shembull, (0; 2: 0) . Sipas formulës së mësipërme për kosinusin e këndit midis planeve, marrim: