Hogyan lehet megszabadulni az irracionalitástól törtekben. Irracionális számok

A számok megértése különösen természetes számok, az egyik legrégebbi matematikai "készség". Sok civilizáció, még a modern civilizációk is, bizonyos misztikus tulajdonságokat tulajdonítottak a számoknak a természet leírásában betöltött óriási jelentőségük miatt. Bár modern tudományés a matematika nem erősíti meg ezeket a „mágikus” tulajdonságokat, a számelmélet jelentősége tagadhatatlan.

A történelem során először sokféle természetes szám jelent meg, majd meglehetősen gyorsan törteket és pozitív irracionális számokat adtak hozzájuk. A nulla és a negatív számok a halmaz ezen részhalmazai után kerültek bevezetésre valós számok. Utolsó készlet, készlet komplex számok, csak a modern tudomány fejlődésével jelent meg.

A modern matematikában a számokat nem történelmi sorrendben vezetik be, bár elég közel állnak hozzá.

Természetes számok $\mathbb(N)$

A természetes számok halmazát gyakran úgy jelölik, hogy $\mathbb(N)=\lkapcsos zárójel 1,2,3,4... \rkapcsos zárójel $, és gyakran nullával töltik ki a $\mathbb(N)_0$ jelölésére.

A $\mathbb(N)$ az összeadás (+) és a szorzás ($\cdot$) műveleteit határozza meg a következő tulajdonságokat bármely $a,b,c\mathbb(N)$-ban:

1. $a+b\in \mathbb(N)$, $a\cdot b \in \mathbb(N)$ a $\mathbb(N)$ halmaz zárva van az összeadás és szorzás műveletei alatt
2. $a+b=b+a$, $a\cdot b=b\cdot a$ kommutativitás
3. $(a+b)+c=a+(b+c)$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$ asszociativitás
4. $a\cdot (b+c)=a\cdot b+a\cdot c$ eloszlás
5. $a\cdot 1=a$ egy semleges elem a szorzáshoz

Mivel a $\mathbb(N)$ halmaz tartalmaz egy semleges elemet a szorzáshoz, de nem az összeadáshoz, ha ehhez a halmazhoz nullát adunk, akkor a halmaz tartalmaz egy semleges elemet az összeadáshoz.

E két művelet mellett a „kevesebb, mint” relációk ($

1. $a b$ trichotómia
2. ha $a\leq b$ és $b\leq a$, akkor $a=b$ antiszimmetria
3. ha $a\leq b$ és $b\leq c$, akkor $a\leq c$ tranzitív
4. ha $a\leq b$ akkor $a+c\leq b+c$
5. ha $a\leq b$ akkor $a\cdot c\leq b\cdot c$

Egész számok $\mathbb(Z)$

Példák egész számokra:
$1, -20, -100, 30, -40, 120...$

Az $a+x=b$ egyenlet megoldásához, ahol $a$ és $b$ ismert természetes számok, $x$ pedig ismeretlen természetes számok, egy új művelet – a kivonás(-) – bevezetése szükséges. Ha van egy $x$ természetes szám, amely kielégíti ezt az egyenletet, akkor $x=b-a$. Azonban ez fajlagos egyenlet nem feltétlenül rendelkezik megoldással a $\mathbb(N)$ halmazon, ezért gyakorlati megfontolások megkövetelik, hogy a természetes számok halmazát kibővítsük, hogy belefoglaljuk egy ilyen egyenlet megoldásait is. Ez egy egész számkészlet bevezetéséhez vezet: $\mathbb(Z)=\lbrace 0,1,-1,2,-2,3,-3...\rbrace$.

Mivel a $\mathbb(N)\subset \mathbb(Z)$, logikus, hogy a korábban bevezetett $+$ és $\cdot$ műveletek és a $ 1 relációk. $0+a=a+0=a$ van egy semleges elem a kiegészítéshez
2. $a+(-a)=(-a)+a=0$ létezik ellentétes szám$-a$ $a$-ért

5. ingatlan:
5. ha $0\leq a$ és $0\leq b$, akkor $0\leq a\cdot b$

A $\mathbb(Z)$ halmaz is zárva van a kivonási művelet alatt, azaz $(\forall a,b\in \mathbb(Z))(a-b\in \mathbb(Z))$.

Racionális számok $\mathbb(Q)$

Példák racionális számok:
$\frac(1)(2), \frac(4)(7), -\frac(5)(8), \frac(10)(20)...$

Tekintsük most az $a\cdot x=b$ alakú egyenleteket, ahol $a$ és $b$ ismert egész számok, $x$ pedig ismeretlen. A megoldáshoz be kell vezetni az osztási műveletet ($:$), és a megoldás $x=b:a$, azaz $x=\frac(b)(a)$ . Ismét felmerül a probléma, hogy a $x$ nem mindig tartozik a $\mathbb(Z)$-hoz, ezért az egész számok halmazát ki kell bővíteni. Ez bevezeti a $\mathbb(Q)$ racionális számok halmazát $\frac(p)(q)$ elemekkel, ahol $p\in \mathbb(Z)$ és $q\in \mathbb(N)$. A $\mathbb(Z)$ halmaz egy olyan részhalmaz, amelyben minden elem $q=1$, ezért $\mathbb(Z)\subset \mathbb(Q)$ és az összeadás és szorzás műveletei erre a halmazra terjednek ki a szerint. szabályokat követve, amelyek megőrzik az összes fenti tulajdonságot a $\mathbb(Q)$ halmazon:
$\frac(p_1)(q_1)+\frac(p_2)(q_2)=\frac(p_1\cdot q_2+p_2\cdot q_1)(q_1\cdot q_2)$
$\frac(p-1)(q_1)\cdot \frac(p_2)(q_2)=\frac(p_1\cdot p_2)(q_1\cdot q_2)$

A felosztás a következőképpen kerül bevezetésre:
$\frac(p_1)(q_1):\frac(p_2)(q_2)=\frac(p_1)(q_1)\cdot \frac(q_2)(p_2)$

A $\mathbb(Q)$ halmazon az $a\cdot x=b$ egyenlet van az egyetlen megoldás minden $a\neq 0$ esetén (a nullával való osztás nincs meghatározva). Ez azt jelenti, hogy van egy inverz $\frac(1)(a)$ vagy $a^(-1)$ elem:
$(\forall a\in \mathbb(Q)\setminus\lbrace 0\rbrace)(\exists \frac(1)(a))(a\cdot \frac(1)(a)=\frac(1) (a)\cdot a=a)$

A $\mathbb(Q)$ halmaz sorrendje a következőképpen bővíthető:
$\frac(p_1)(q_1)

A $\mathbb(Q)$ halmaznak van egy fontos tulajdon: Bármely két racionális szám között végtelenül sok más racionális szám van, ezért nincs két szomszédos racionális szám, ellentétben a természetes számok és egész számok halmazával.

Irracionális számok $\mathbb(I)$

Példák irracionális számokra:
$0.333333...$
$\sqrt(2) \kb. 1,41422135...$
$\pi\kb. 3,1415926535...$

Mivel bármely két racionális szám között végtelenül sok más racionális szám található, könnyen levonható téves következtetés, hogy a racionális számok halmaza olyan sűrű, hogy nem kell tovább bővíteni. Még Püthagorasz is elkövetett ilyen hibát annak idején. Kortársai azonban már cáfolták ezt a következtetést, amikor a $x\cdot x=2$ ($x^2=2$) egyenlet megoldásait tanulmányozták a racionális számok halmazán. Egy ilyen egyenlet megoldásához be kell vezetni a négyzetgyök fogalmát, majd ennek az egyenletnek a megoldása $x=\sqrt(2)$ alakú. Egy olyan egyenletnek, mint például $x^2=a$, ahol $a$ egy ismert racionális szám, és $x$ egy ismeretlen, nem mindig van megoldása a racionális számok halmazára, és ismét felmerül az igény a készlet. Irracionális számok halmaza keletkezik, és ehhez a halmazhoz tartoznak az olyan számok, mint a $\sqrt(2)$, $\sqrt(3)$, $\pi$....

Valós számok $\mathbb(R)$

A racionális és irracionális számok halmazának uniója a valós számok halmaza. Mivel a $\mathbb(Q)\subset \mathbb(R)$, ismét logikus azt feltételezni, hogy a bevezetett aritmetikai műveletek és relációk megtartják tulajdonságaikat az új halmazon. Ennek formális bizonyítása nagyon nehéz, ezért a valós számok halmazán az aritmetikai műveletek és relációk fent említett tulajdonságait axiómaként vezetjük be. Az algebrában egy ilyen objektumot mezőnek nevezünk, így a valós számok halmazát rendezett mezőnek mondjuk.

Ahhoz, hogy a valós számok halmazának meghatározása teljes legyen, be kell vezetni egy további axiómát, amely megkülönbözteti a $\mathbb(Q)$ és a $\mathbb(R)$ halmazokat. Tegyük fel, hogy $S$ a valós számok halmazának nem üres részhalmaza. A $b\in \mathbb(R)$ elemet egy $S$ halmaz felső korlátjának nevezzük, ha a $\forall x\in S$ értéke $x\leq b$. Ekkor azt mondjuk, hogy a $S$ halmaz fent korlátos. Legkevésbé felső határ a $S$ halmazból a felső összeget nevezzük, és a $\sup S$ jelöléssel. A fogalmakat hasonlóan vezetjük be alsó határ, egy alul határolt halmaz és egy infinum $\inf S$ . Most megfogalmazódik a hiányzó axióma alábbiak szerint:

A valós számok halmazának bármely nem üres és felső korlátos részhalmazának van felsőbbsége.
Az is igazolható, hogy a fenti módon meghatározott valós számok mezője egyedi.

Komplex számok$\mathbb(C)$

Példák komplex számokra:
$(1, 2), (4, 5), (-9, 7), (-3, -20), (5, 19),...$
$1 + 5i, 2 - 4i, -7 + 6i...$ ahol $i = \sqrt(-1)$ vagy $i^2 = -1$

A komplex számok halmaza a valós számok összes rendezett párját reprezentálja, azaz $\mathbb(C)=\mathbb(R)^2=\mathbb(R)\times \mathbb(R)$, amelyen a az összeadás és a szorzás meghatározása a következőképpen történik:
$(a,b)+(c,d)=(a+b,c+d)$
$(a,b)\cdot (c,d)=(ac-bd,ad+bc)$

A komplex számok írásának többféle formája létezik, ezek közül a legelterjedtebb a $z=a+ib$, ahol az $(a,b)$ egy valós számpár, a $i=(0,1)$ szám pedig képzeletbeli egységnek nevezzük.

Könnyen kimutatható, hogy $i^2=-1$. A $\mathbb(R)$ halmaznak a $\mathbb(C)$ halmazra való kiterjesztése lehetővé teszi, hogy meghatározzuk a négyzetgyökét negatív számok, ez volt az oka a komplex számok halmazának bevezetésének. Az is könnyen kimutatható, hogy a $\mathbb(C)$ halmaz egy részhalmaza, amelyet a $\mathbb(C)_0=\lbrace (a,0)|a\in \mathbb(R)\rbrace$ ad meg, kielégíti a valós számok összes axiómáját, ezért $\mathbb(C)_0=\mathbb(R)$ vagy $R\subset\mathbb(C)$.

A $\mathbb(C)$ halmaz algebrai szerkezete az összeadás és szorzás műveletei tekintetében a következő tulajdonságokkal rendelkezik:
1. összeadás és szorzás kommutativitása
2. összeadás és szorzás asszociativitása
3. $0+i0$ - semleges elem az összeadáshoz
4. $1+i0$ - semleges elem a szorzáshoz
5. A szorzás az összeadáshoz képest disztributív
6. Egyetlen inverz van az összeadásra és a szorzásra is.

Minden racionális szám közönséges törtként ábrázolható. Ez vonatkozik az egész számokra (például 12, –6, 0), és véges tizedes törtekre (például 0,5; –3,8921), valamint végtelen periodikus tizedes törtekre (például 0,11(23); –3 , (87) )).

Viszont végtelen nem periodikus tizedesjegyek formában képviseli közönséges törtek lehetetlen. Ilyenek irracionális számok(vagyis irracionális). Ilyen szám például a π szám, amely megközelítőleg egyenlő 3,14-gyel. Azt azonban nem lehet meghatározni, hogy pontosan mivel egyenlő, mivel a 4-es szám után végtelen sora van további számoknak, amelyekben nem lehet megkülönböztetni az ismétlődő periódusokat. Sőt, bár a π számot nem lehet pontosan kifejezni, de van egy sajátossága geometriai jelentése. A π szám bármely kör hosszának és átmérőjének hosszának aránya. Így az irracionális számok valójában léteznek a természetben, akárcsak a racionális számok.

Az irracionális számok másik példája a négyzetgyök pozitív számok. A gyökök számokból való kiemelése önmagában ad racionális értékek, másoktól - irracionális. Például √4 = 2, azaz a 4 gyöke racionális szám. De √2, √5, √7 és még sokan mások irracionális számokat eredményeznek, vagyis csak közelítéssel, bizonyos tizedesjegyre kerekítve kinyerhetők. Ebben az esetben a tört nem periodikussá válik. Vagyis nem lehet pontosan és határozottan megmondani, hogy miért egyenlő a gyökérrel ezekből a számokból.

Tehát √5 a 2 és 3 között fekvő szám, mivel √4 = 2 és √9 = 3. Arra is következtethetünk, hogy √5 közelebb van 2-hez, mint 3-hoz, mert √4 közelebb van √5-höz, mint √9 és √5 között. Valóban, √5 ≈ 2,23 vagy √5 ≈ 2,24.

Az irracionális számokat más számításokban is megkapjuk (és nem csak a gyökök kinyerésekor), és negatívak is lehetnek.

Az irracionális számokkal kapcsolatban azt mondhatjuk, hogy bármilyen egységnyi szegmenst veszünk is az ilyen számmal kifejezett hossz mérésére, nem tudjuk biztosan mérni.

Az aritmetikai műveletekben az irracionális számok is részt vehetnek a racionális számokkal együtt. Ugyanakkor számos törvényszerűség van. Például, ha egy aritmetikai műveletben csak racionális számok vesznek részt, akkor az eredmény mindig racionális szám. Ha csak irracionálisak vesznek részt a műveletben, akkor nem lehet egyértelműen megmondani, hogy az eredmény racionális vagy irracionális szám lesz.

Például, ha megszoroz két irracionális számot √2 * √2, akkor 2-t kap – ez egy racionális szám. Másrészt √2 * √3 = √6 irracionális szám.

Ha egy aritmetikai művelet racionális és irracionális számokat tartalmaz, akkor az eredmény irracionális lesz. Például 1 + 3,14... = 4,14... ; √17-4.

Miért irracionális szám a √17 – 4? Képzeljük el, hogy kapunk egy x racionális számot. Ekkor √17 = x + 4. De x + 4 racionális szám, mert azt feltételeztük, hogy x racionális. A 4-es szám is racionális, tehát x + 4 racionális. Egy racionális szám azonban nem lehet egyenlő a √17 irracionális számmal. Ezért hibás az a feltételezés, hogy √17 – 4 racionális eredményt ad. Egy aritmetikai művelet eredménye irracionális lesz.

Van azonban kivétel ez alól a szabály alól. Ha egy irracionális számot megszorozunk 0-val, akkor 0 racionális számot kapunk.

Az irracionális számok halmazát általában nagybetűvel jelöljük latin betű I (\displaystyle \mathbb (I) ) félkövér stílusban, árnyékolás nélkül. Így: I = R ∖ Q (\displaystyle \mathbb (I) =\mathbb (R) \backslash \mathbb (Q) ), vagyis az irracionális számok halmaza a valós és a racionális számok halmaza közötti különbség.

Az irracionális számok, pontosabban az egységnyi hosszúságú szegmenssel összemérhetetlen szegmensek létezését már az ókori matematikusok is ismerték: ismerték például a négyzet átlójának és oldalának összemérhetetlenségét, ami egyenértékű a négyzet irracionalitásával. a szám.

Enciklopédiai YouTube

1 / 5
Irracionálisak a következők:

Példák az irracionalitás bizonyítására

2 gyöke

Tegyük fel az ellenkezőjét: 2 (\displaystyle (\sqrt (2))) racionális, azaz törtként ábrázolva m n (\displaystyle (\frac (m)(n))), Hol m (\displaystyle m) egy egész szám, és n (\displaystyle n)- természetes szám.
Nézzük négyzetre a feltételezett egyenlőséget:
2 = m n ⇒ 2 = m 2 n 2 ⇒ m 2 = 2 n 2 (\displaystyle (\sqrt (2))=(\frac (m)(n))\Jobbra 2=(\frac (m^(2) ))(n^(2)))\Jobbra m^(2)=2n^(2)).
Történet

Antikvitás

Az irracionális számok fogalmát az indiai matematikusok implicit módon átvették a Kr.e. 7. században, amikor Manava (i. e. 750 körül - ie 690 körül) rájött, hogy egyes természetes számok, például 2 és 61 négyzetgyöke nem fejezhető ki egyértelműen. [ ] .
Az irracionális számok létezésének első bizonyítékát általában Metapontoszi Hippasosznak (i. e. 500 körül), egy pitagorasznak tulajdonítják. A pitagoreusok idején azt hitték, hogy létezik egyetlen hosszúságegység, amely kellően kicsi és oszthatatlan, és amely egész számú alkalommal tartalmaz bármely szakaszt [ ] .
Arról nincs pontos adat, hogy Hippasus melyik számot bizonyította irracionálisnak. A legenda szerint a pentagram oldalainak hosszának tanulmányozásával találta meg. Ezért joggal feltételezhető, hogy ez volt az aranymetszés [ ] .
A görög matematikusok ezt az arányt összemérhetetlen mennyiségeknek nevezték alogos(kimondhatatlan), de a legendák szerint nem rótták kellő tiszteletüket Hippasusnak. Van egy legenda, amely szerint Hippasus felfedezésben volt része tengeri utazás, és más pitagoreusok a fedélzetre vetették "az univerzum egy olyan elemének létrehozása miatt, amely tagadja azt a tant, hogy az univerzumban minden entitás egész számokra és azok arányaira redukálható". Hippasus felfedezése megkérdőjelezte a pitagoraszi matematikát komoly probléma, megsemmisítve az egész elmélet alapjául szolgáló feltételezést, miszerint a számok és a geometriai objektumok egyek és elválaszthatatlanok.

Első fejezet.

Az irracionális szám fogalma.

183. Egységgel arányos és össze nem mérhető mennyiségek.

Amint a geometriából ismeretes, két egyenes szakasz, vagy két szög, vagy két azonos sugarú ív közös mértéke, általában két azonos és három mennyiségi érték ennek a mennyiségnek az értéke, amelyet tartalmaz. mindegyikben egész számú alkalommal maradék nélkül. A geometriában elmagyarázzák, hogy lehet két olyan szakasz, amelynek nincs közös mértéke (például egy négyzet oldala és átlója).

Az azonos mennyiségű két értéket egymással arányosnak vagy össze nem mérhetőnek nevezzük, attól függően, hogy van-e közös mértékük vagy sem.

184. A mérés fogalma. Tegyük fel, hogy meg akarja mérni egy szakasz hosszát AB hosszegység segítségével CD .

Ehhez megtudjuk, hányszor egy egység CD tartalmazza AB . Kiderül, hogy benne van AB 3-szor némi maradékkal EV , kisebb CD . Ekkor a 3-as szám közelítő mérési eredmény lesz 1-es pontossággal, és ráadásul hátrányos is, mivel AB több 3 CD , de kevésbé 4 CD (a 4-es szám közelítő mérési eredménynek is nevezhető 1-es pontossággal, de többlettel).

Ha pontosabb mérési eredményt szeretnénk kapni, megtudjuk, hányszoros a maradék EV az egység töredékét tartalmazza CD , pl. 1/10 CD . Tegyük fel, hogy ez a tört benne van EV több mint 8, de kevesebb, mint 9-szer. Ekkor a 3,8 és 3,9 számok a szegmens mérésének hozzávetőleges eredményei AB 1/10 pontossággal az első szám hiányos, a második többlet.

Még pontosabb mérési eredményt szeretnénk megtudni, hogy az utolsó maradék hányszor tartalmazza az 1/100-at. Egységrészesedés CD . Tegyük fel, hogy ez a tört több mint 5-ször, de kevesebb mint 6-szor szerepel a maradékban. Ekkor a 3,85 és 3,86 számok a szegmens mérésének hozzávetőleges eredményei AB 1/100 egység pontossággal. Ezt a mérést mindaddig folytathatja, amíg vagy nincs maradék, vagy a maradék olyan kicsi lesz, hogy elhanyagolható; az első esetben egy pontos mérési eredményt kapunk, a második esetben egy hozzávetőlegeset az egységnek azon töredékének pontosságával, amellyel legutóbb mértük.

Ha a szegmens AB aránytalan egy hosszegységhez CD , Azt pontos eredmény soha nem kaphatunk méréseket. Valóban, ha feltételezzük, hogy egy ilyen eredmény például egy töredék lenne. 59/27, majd 1/27 részesedés CD általános intézkedésként szolgálna AB ÉS CD , és az össze nem mérhető szegmenseknek nincs közös mértékük.

Ha a szegmens AB arányos CD , akkor pontos mérési eredményt kaphatnánk, ha először találtunk volna egy általános mértéket a AB És CD és megtudta, hányszor van benne AB És CD . Ha, tegyük fel, az általános mérték be AB 23-szor tartalmazza, és ben CD akkor 11-szer AB = 23/11 egység CD . Ám ha általános mérték keresése nélkül az egység tetszőlegesen vett törtrészeivel mérünk, akkor gyakran előfordulhat, hogy még ebben az esetben sem kapunk pontos mérési eredményt.

A mérés leggyakrabban egy egység tizedesjegyében történik; akkor a mérési eredményt tizedes törtként fejezzük ki. Ha a mért szakasz arányos egy hosszegységgel, akkor a tizedes tört lehet véges (ha az általános mérték az egység tizedes törtrésze) vagy végtelen (ha az általános mérték az egységnek olyan törtrésze, amely nem pontos tizedes törtté alakítjuk). Ha a mért szakasz nem arányos egy hosszegységgel, akkor a mérésnek nem lehet pontos eredménye, ezért a tizedes törtnek végtelennek kell lennie (ha a mérés végtelenül folytatódik).

Hasznos megjegyezni, hogy szignifikáns különbség van az arányos szegmens méréséből nyerhető végtelen tizedes tört és az össze nem mérhető szakasz méréséből származó között. Az első törtnek periodikusnak, a másodiknak nem periodikusnak kell lennie.

185. Irracionális számok. A számok egész számok, törtek, véges tizedesjegyek és periodikus tizedesjegyek. köznév racionális számok; decimális végtelen törtek a nem periodikusakat nevezzük irracionális számok. Az előbbiek az egységgel arányos mennyiségek, az utóbbiak az egységgel összemérhetetlen mennyiségek mérőszámaként szolgálnak.

Egy irracionális szám akkor tekinthető ismertnek (vagy adottnak), ha olyan módszert adunk meg, amellyel tetszőleges számú tizedesjegy megtalálható.

Két irracionális szám (mint két racionális) akkor tekinthető egyenlőnek, ha két egyenlő mennyiség ugyanazzal az egységgel való méréséből származik; Két egyenlőtlen szám közül a nagyobbat tekintjük a nagyobb mennyiség méréséből származónak. Két egyenlő értékeket természetesen tartalmaznia kell ugyanaz a szám egész egységek, ugyanannyi tized, ugyanannyi század stb., ezért az egyenlő irracionális számokat ugyanazokkal a számokkal kell kifejezni. Egy nagyobb értéknek több egész számot kell tartalmaznia, vagy - ha az egész számok egyenlőek, akkor nagyobb számú tizedet, vagy - ha az egészek és a tizedek egyenlőek - nagyobb számot, századot stb. Például a 2,745037 számot. .. nagyobb, mint a 2 ,745029..., mivel az elsőben a 6. számjegy a másodikban lévő 6. számjegynél nagyobb számot fejez ki, ha minden előző számjegy azonos.

Az irracionális számok lehetnek pozitívak vagy negatívak, attól függően, hogy pozitívnak vagy negatívnak tekintett mennyiségeket mérnek.

186. Irracionális szám közelítő értékei. Adjunk valami irracionális számot α , azaz jelöljünk meg egy módszert, amellyel egy számból annyi számjegyet kaphatunk, amennyit akarunk α (ez a módszer lehet például az a szabály, amely alapján közelítő négyzetgyököket találunk 1/10-től 1/100-ig 1/1000-ig stb.). Tegyük fel, hogy megtaláltuk egy szám következő 5 számjegyét α :

α = 1,4142...

Vegyük ezek közül az első néhány számot, például az 1,41-es számokat, a többit pedig dobjuk el. Ekkor megkapjuk a szám hozzávetőleges értékét α , és ennek az értéknek hátránya lesz, mivel 1,41< α . Ha a megtartott számjegyek közül az utolsót megnöveljük 1-gyel, azaz 1,41 helyett 1,42-t veszünk, akkor a szám közelítő értékét is kapjuk α , de túlzottan. Általában két közelítő értékből, amelyek közül az egyik hiányos, a másik többlet, a hiányos értéket veszik, ha az eldobott számjegyek közül az első kisebb, mint 5, és a többletet tartalmazó értéket, ha ez a számjegy nagyobb, mint 5.

187. Irracionális számokra vonatkozó cselekvések meghatározása. Hadd α És β lesz néhány adott pozitív irracionális szám. Ha ezeket a számokat megadjuk, ez azt jelenti, hogy bármilyen pontossággal megtaláljuk hozzávetőleges értéküket. Legyen például a számok hozzávetőleges értéke α És β , hátrányosan figyelembe véve a következő lesz (közelítő értéket vesszük √3 és √2):

(A megfelelő közelítéseket ezekből a számokból felesleggel kapjuk, ha az utolsó tizedesjegyet 1-gyel növeljük.)

Majd: A) hajtogatni α És β azt jelenti, hogy meg kell találni egy számot, amely az lenne

azaz Az α és β számok összeadása azt jelenti, hogy találunk egy harmadik számot, amely az lenne több, mint az összeg bármely hozzávetőleges érték, amelyet hiányossággal vettek fel, de kisebb, mint a felesleggel vett közelítő értékek összege.

b) Hozzávetőleges számokat véve α És β most jeleztük, azt mondhatjuk, hogy a termék α β van egy szám

vagyis az α és β számokat megszorozni azt jelenti, hogy találunk egy harmadik számot, amely nagyobb lenne bármelyik közelítő értékük szorzatánál, hátrányosan felvéve, de kevesebb termék a túlzottan vett hozzávetőleges értékeket.

V) Az α irracionális számot a második, harmadik, negyedik stb. hatványra emelni azt jelenti, hogy két, három, négy stb. tényezőből álló szorzatot találunk, amely egyenlő α-val.

d) Az irracionális számokra az inverz cselekvéseket ugyanúgy definiáljuk, mint a racionális számokra; szóval vonjuk ki a számból α szám β egy ilyen szám megtalálását jelenti X hogy az összeg β + X egyenlő α stb.

Ha az egyik szám α vagy β racionális lesz, akkor be a fenti definíciókat közvetlen cselekvések esetén egy ilyen szám hozzávetőleges értékei helyett a pontos számot vehetjük fel.

Egy irracionális szám és nulla szorzatát a racionális számokhoz hasonlóan nullának tekintjük.

A negatív irracionális számokra vonatkozó műveleteket a racionális negatív számokra megadott szabályok szerint hajtjuk végre.

Közelebbről megvizsgálva megállapítható, hogy Az irracionális számokra vonatkozó műveletek ugyanazokkal a tulajdonságokkal rendelkeznek, mint a racionális számokra vonatkozó műveletek ; például az összeg és a szorzat kommutatív és asszociatív tulajdonságokkal rendelkezik; termék és divízió ezen kívül is rendelkezik elosztó tulajdon. Az egyenlőtlenségekkel kifejezett tulajdonságok az irracionális számoknál is megmaradnak; tehát ha α > β , Azt α + γ > β, αγ > βγ (Ha γ > 0) és αγ < βγ (Ha γ < 0), stb.

Második fejezet.

A gyökök irracionális jelentései.

188. Bármilyen fok közelítő gyökerei. Azt már elmondtuk (7. osztály 2. fejezet 175-177. §), hogy mik a közelítő négyzetgyökök 1-ig, 1/10-ig stb. és hogyan helyezkednek el ezek a gyökerek. A négyzetgyökről akkor elmondottak bármely más fok gyökére vonatkoztathatók. Például a közelítő 3 √2 1/100 pontossággal olyan tizedes tört, amely egészből, tizedből és századból áll, amelynek kocka kisebb, mint 2, de ha növeljük 1/100-al és emeljük, akkor ez megnő. tört egy kockára, több 2-t kapunk.

Nem fogunk szabályokat levezetni a köbös és egyéb egyebek pontos és közelítő gyökereinek megtalálására magas fokok; Korlátozzuk magunkat a következőkre egyszerű trükk hogy olyan gyökereket találjunk. Hadd kell megtalálnod a 3 √2-t. A hozzávetőleges gyökök 1-es pontossággal nyilvánvalóan az 1-es (hiányos) és a 2-es számok (felesleggel) lesznek. A kívánt gyökér tizedeinek számának meghatározásához a sorozatban találjuk:

1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2

kettő egymás mellett megéri a számokatúgy, hogy a bal oldali szám kockája kisebb, mint 2, a jobbé pedig nagyobb, mint 2. Ehhez vegyük ki a sorozatunkban szereplő számok közül az 1,5-ös átlagot, és emeljük a kockára. A következőt fogjuk találni: 1,5 3 = 3,375, ami nagyobb, mint 2. Mivel az 1,5-től jobbra lévő számok kockába emelve még többet adnak, a sorozat teljes jobb felét eldobhatjuk, és csak a számokat tesztelhetjük:

1; 1,1; 1,2; 1,3; 1,4.

Vegyük ezek átlagát 1,2-t, és emeljük a kockára. 1,728-at kapunk, ami kevesebb, mint 2. Ez azt jelenti, hogy most már csak az 1,3 és 1,4 számokat teszteljük. Az 1,3-as számot kockává emelve 2,197-et kapunk, ami nagyobb, mint 2. Így két 1,2-es és 1,3-as számot kaptunk, amelyek 0,1-el különböznek egymástól, és amelyek között a 2-es szám szerepel hozzávetőleges köbgyökér 2 1/10 pontossággal hiány és többlet mellett. Ha meg akarjuk találni a százados számjegyet, akkor a következő számokkal kell próbálkoznunk:

1,21; 1,22; 1,23;.......1,29.

A sorozat átlagos 1,25-ös számát kockává emelve a következőt kapjuk: 1,25 3 = 1,953125, ami kisebb, mint 2. Ez azt jelenti, hogy most már csak a következő számokat kell tesztelnünk: 1,26; 1,27; 1,28; 1.29. Mivel az 1,25 3 nagyon kevéssé különbözik a 2-től, nagyon valószínű, hogy 1,26 3 nagyobb lesz, mint 2. És valóban, ha 1,26-ot emelünk a kockára, 2,000376-ot kapunk. Ez azt jelenti, hogy a 2 kívánt kockagyöke 1/100 pontossággal 1,25 (hiánnyal) vagy 1,26 (többlettel) lesz. Ha tovább akarjuk keresni az ezredszámokat, hasonló módon kellene tesztelnünk a sorozatok számait:

1,251; 1,252; 1,253;.........1,259.

Természetesen ez a technika unalmas (több is van kényelmes módokon), de világosan mutatja, hogy bármely fok közelítő gyökének tizedesjegyei tetszőleges nagy számban megtalálhatók.

189. A gyök irracionális jelentése. Tisztázzuk, hogy √3, ami határozottan nem egész számként vagy vagy törtszám, egyenlő némelyikkel irracionális szám. Ehhez közelítő √3 sorozatot számítunk ki 1/10 pontossággal 1/100-ig, 1/1000-ig...

Ezek az értékek a következők lesznek:

1,7; 1,73; 1,732; 1,7320 (hétről).

1,8; 1,74; 1,733; 1,7321 (kivéve).

Ábrázoljuk ezeket a számokat egy számegyenesen. Ehhez egy bizonyos egyenesen egy A pontot veszünk a szakaszok kezdeteként, és tetszőleges hosszegységet választva ábrázoljuk a szakaszokat az egyenesen: Ab 1 = 1,7 , Ab 2 = 1,73 stb.; majd a szegmensek: Ab 1 = 1,8, Ab 2 =1,74 stb.

Mivel minden hozzávetőleges hiányos gyökér kisebb, mint minden hozzávetőleges többletgyök (mivel az első négyzete kisebb, mint 3, a második négyzete pedig nagyobb, mint 3), akkor minden lány b minden ponttól balra kell feküdnie IN . Másrészt a különbség a felesleggel rendelkező közelítő gyökér és a megfelelő közelítő hiányos gyökér között tetszőlegesen kicsinyíthető; ezért korlátlanul növelve a pontosságot, amellyel 3 közelítő négyzetgyökét találjuk, a B pontok tartományát a B pontok tartományától elválasztó számegyenesen lévő intervallum (azaz az intervallum b 1 B 1 , b 2 B 2 , b 3 B 3 ..), egyre kisebb lesz, és tetszőleges kicsivé válhat. Ilyen feltételek mellett fel kell tételeznünk, hogy van egy bizonyos pont a vonalon X (és csak egy), amely határként szolgál, amely elválasztja az egyenes azon részét, amelyen az összes pont található b , annak attól a részétől, amelyen az összes pont található IN .

Jelöljük betűvel α szám, amely egy szegmenst mér Ó . Mivel ez a szám nagyobb, mint a szegmenseket mérő számok mindegyike Ab 1 ,Ab 2 ... és kisebb, mint a szegmenseket mérő számok mindegyike AB 1 , AB 2 . . ., Az α 2 nagyobbnak kell lennie, mint az egyes közelítő értékek négyzete négyzetgyökök 3-ból hátrányosan vették, és négyzetnél kisebb mindegyik hozzávetőleges négyzetgyök 3, feleslegben véve. A közelítő négyzetgyök definíciója szerint egy ilyen szám 3. α 2 = 3 és ezért α = √3

Megismételve mindazt, amit az imént mondott o √3, tetszőleges szám bármely fokának gyökeréről (persze pozitív, hiszen arról beszélünk számtani gyökök), mondhatjuk, hogy bármilyen szám legyen is A, Mindig m√A ebből van egy bizonyos szám, racionális vagy irracionális m a th hatvány egyenlőA.

Ezért a gyökök ezen definícióján alapuló összes tulajdonsága (6. szakasz, 6. fejezet, 168. §) az irracionális jelentésükre is vonatkozik. Így bármilyen pozitív szám is legyen, mindig a következők lesznek:

Harmadik fejezet.

A közelítő számítások fogalma.

190. Előzetes megjegyzés. Ha irracionális számokkal (vagy racionális számokkal, ha vannak kifejezve) bármilyen műveletet végrehajt tizedesjegyek nagyon nagy számban számok) meg kell elégedni a cselekvés hozzávetőleges eredményével. Ebben az esetben fontos tudni, hogy ennek a közelítő eredménynek mekkora a hibája. Nézzük meg, hogyan lehet ezt a legegyszerűbb esetekben megtenni.

191. Közelítések hiánnyal és többlettel. Ha egy pontos szám helyett közelítő számot veszünk, akkor ez utóbbit nevezzük hátránnyal közeledik, ha kisebb, mint a pontos szám, és többlettel, ha nagyobb annál. A pontos szám és a közelítés közötti különbséget e közelítés hibájának nevezzük. Ha például a pontos szám 3,826, és e helyett 3,82-t vettünk, akkor ez egy hátrányos közelítés lesz, és a hiba 0,006; ha 3,826 helyett 3,83-at veszünk, akkor lesz egy közelítésünk többlettel, és a hiba 0,004 lesz. Általában a hiba pontos értéke ismeretlen marad, és csak azt tudjuk, hogy kisebb, mint egy bizonyos töredék, például kisebb, mint 1/100. Aztán azt mondják, hogy a közelítés pontosan 1/100-ig.

Legyen például ismert, hogy 2,85 a szám közelítése A 1/100 pontossággal. Ez azt jelenti, hogy a 2,85 különbözik A kevesebb, mint 1/100, tehát ha 2,85 egy közelítés hátrányos, akkor a pontos szám A 2,85 és 2,86 között van, és ha a 2,85 egy közelítés többséggel, akkor A 2,85 és 2,84 között van. A Ha továbbra sem ismert, hogy a 2,85-ös közelítés hiány vagy többlet lesz-e, és csak 1/100 pontosságú, akkor a szám

csak azt mondhatjuk, hogy 2,84 és 2,86 között van. A hibát, amelyről az imént beszéltünk, abszolút hibának nevezzük, ellentétben a relatív hibával, amely az arányra vonatkozik abszolút hiba a pontos számra. Tehát, ha a pontos szám 3,826 helyett a hozzávetőleges 3,82-t vesszük, akkor relatív hiba

0,006 lesz: 3,820 = 6:3826 = 0,001568..., azaz kisebb, mint 0,002. Ez azt jelenti, hogy a 3,82-es közelítéssel kevesebb, mint 0,002-vel maradtunk el a pontos számtól.

Néha a relatív hibát a pontos szám százalékában fejezik ki, vagyis azt jelzik, hogy a hiba kisebb, mint a pontos szám ennyi százaléka. Tehát, ha a relatív hiba kisebb, mint a pontos szám 0,002, akkor ez azt jelenti, hogy kisebb, mint ennek a számnak 0,2%-a, mivel

A jövőben csak abszolút hibáról fogunk beszélni, egyszerűen „hibának” nevezzük. 192. Tizedes közelítések.

A) A tizedes számok kezelésekor ezek közelítését 1/10-ig, 1/100-ig stb., sőt akár 1/2 tizedes egység pontossággal veszik. Az ilyen közelítések a következő szabályok szerint találhatók. Adott hátránnyal közelítést kapni decimális szám (végleges ill végtelen szám

Így a 3,14159... hátrányos közelítés 1/100 pontossággal 3,14, mert ez a szám kisebb, mint a megadott, és a hiba, amely 0,159... egy századdal egyenlő, kisebb, mint a egész századik.

b) Ahhoz, hogy egy adott decimális szám többletével közelítést kapjunk bármely számjegy egy tizedes egységnyi pontosságával, elegendő az összes számjegyet elvetni attól a számtól jobbra, amelyik kifejezi ennek a számjegynek az egységeit, és növelni kell 1 az utolsó megtartott számjegy.

Így egy közelítés a 3,14159... szám többletével 0,001 pontossággal 3,142, mert ez a szám nagyobb, és a hibája kisebb, mint 0,001.

V) Ahhoz, hogy egy adott decimális számot bármely számjegy tizedesegységének 1/2 pontosságú közelítésével kapjunk, elegendő az 1. szabályban leírtak szerint 1-gyel növelni a megtartott számjegyek közül az utolsót, ha a az eldobott számjegyek közül az első 5 vagy több 5 (és akkor a megközelítés bőséges lesz), és egyébként hagyjuk változatlanul (és akkor a közelítés hátrányos lesz).

Így a 3,14159... szám közelítése (hátrányával) 1/2 százados pontossággal 3,14, mivel a hiba kisebb, mint 0,5 század; ugyanennek a számnak a közelítése (többlettel) 1/2 ezrelékes pontossággal 3,142, mivel az (1-0,59) ezrednek megfelelő hiba nyilvánvalóan kisebb, mint 0,5 ezred.

193. Hiba a hozzávetőleges összegben. Az aritmetikai összeadás tulajdonságaiból tudjuk, hogy ha bármely tag egy bizonyos számmal csökken vagy nő, akkor az összeg ugyanennyivel csökken vagy nő. Ezért, ha az összes kifejezést hiányossággal vagy többséggel veszik fel, akkor az összeg az első esetben hiányos lesz, a második esetben pedig többlet, és az összeg hibája megegyezik az összeg összegével. az összes kifejezés hibáit. Ha megtörténik, hogy egyes kifejezéseket hiányossággal, másokat többlettel veszünk, akkor a hiányos kifejezésekből eredő hibát részben vagy egészben fedezi a túlsúlyos kifejezések ellentétes hibája, tehát a végső hiba. összege kisebb, mint a kifejezések hibáinak összege. Íme néhány példa:

A) Tegyük fel, hogy meg kell találnunk az összegeket:

√2 + √3 + √5 = 1,4142 . . . + 1,7320 . . . + 2,2360 . . .

Tegyük fel, hogy minden tagban a tizedesvessző után három tizedesjegyre korlátozódnak:

Mivel az összes kifejezést hátrányosan vettük, akkor az összeg is hátrányos lesz; az egyes tagok hibája kisebb, mint 1/2 ezredrész, ezért az 5,382 összeg hibája kisebb, mint (1/2 + 1/2 + 1/2) ezredrész, azaz. kevesebb, mint 1,5 ezrelék. Ha az 5,382 szám utolsó 2-es számjegyét elvetjük, akkor az összeget tovább csökkentjük 2 ezrelékkel, és az 5,38 szám hibája kisebb lesz, mint az 1,5 + 2 = 3,5 ezrelék összege, ami viszont kisebb, mint 5 ezredrész, azaz kevesebb, mint 3/g századrész. Így az 5,38 ezeknek a kifejezéseknek a hozzávetőleges összege, hiányossággal és 1/2 századi pontossággal.

Ekkor a 10,9005 összeg hibája mindenképpen kisebb lesz
1/2 + 1/2 + 1/2 + 1/2 + 1/2 = 2,5 tízezrelék; ha ennek az összegnek az utolsó 5-ös számjegyét elvetjük, akkor 5 tízezreddel csökkentjük, és a hiba kisebb lesz, mint 5 + 2,5 = 7,5 tízezrelék, ami kevesebb, mint 10 tízezrelék, azaz. kevesebb, mint 1 ezrelék. Így a 10 900-as szám egy hozzávetőleges, hátrányos összeg (mivel az 5 tízezrelékes csökkenés nagyobb, mint a lehetséges 2,5 tízezrelékes növekedés), 1 ezrelék pontossággal.

Ezekből a példákból jól látható, hogy ha valamilyen számjegy egységnyire pontos közelítő összeget kell találnunk, akkor több tizedesjegyet kell beírnunk a kifejezésekbe, mint amennyi a végeredményben kell (1 számjeggyel többet, ha nincs több mint 10 kifejezés). Tegyük fel például, hogy meg kell találnia az összeget 1 század pontossággal:

Figyeljük meg, hogy néha a hozzávetőleges összeg utolsó számjegyét meg kell növelni 1-gyel. Tegyük fel például, hogy a most megadott példában a 95,534 összeg harmadik tizedesjegye nem 4, hanem 9; akkor ezt elvetve 95,53-at kapnánk hátránnyal, 6 + 9 = 15 ezrelék pontossággal, ami 1,5 század. Ha az utolsó tizedesjegyet megnöveljük 1-gyel, azaz felvesszük a 95,54-es számot, akkor nyilvánvalóan 1 századdal csökkentjük a hibát, aminek eredményeként az immár kevesebb lesz, mint 1 század (de nem tudni, hogy a hozzávetőleges összeg alatt vagy felett lesz).

194. Hozzávetőleges különbség hibája. Az aritmetikai kivonás tulajdonságaiból tudjuk, hogy ha csökkentjük vagy növeljük a minuendet, akkor a különbség ugyanannyival csökken vagy nő; Ha csökkentjük vagy növeljük a kivonandót, akkor a különbség ugyanannyival nő vagy csökken. Ez azt jelenti, hogy ha egy szám kivonásához mindkét adatot hiányossággal vagy mindkettőt többlettel vesszük, akkor a különbség hibája megegyezik az adott számok hibáinak különbségével; ha egy adott szám hiányossággal, egy másikat pedig többlettel vesszük, akkor a különbség hibája egyenlő legyen ezen számok hibáinak összegével. Íme néhány példa:

1) √3 - √2 = 1,73205 ... - 1,41421

Tegyük fel, hogy minden számban csak 3 tizedesjegyet tettünk a tizedesvessző után:

Mivel mindkét közelítést 1/2 ezred pontosságú hiányossággal vettük, akkor a 0,318-as szám hibája, amely megegyezik e számok hibáinak különbségével, kisebb, mint 1/2 ezredrész, és továbbra sem ismert, hogy a közelítő különbség hiány vagy többlet esetén lesz (nem ismert, hogy melyik csökkenés nagyobb: a csökkentett vagy a kivonandó).

2) Meg kell találni a 7,283-5,496 közelítő számok közötti különbséget, 1 ezrelékre pontosan, és nem tudni, hogy mindkettőt hiányossággal, vagy mindkettőt többlettel, vagy az egyiket hiányossággal vettük-e és a más felesleggel.

Így, ha meg kell találnia a megadott közelítő számok közötti különbséget egy egységnyi számjegy pontossággal, akkor az adott számokban korlátozhatja magát ennek a számjegynek az egységeire, és minden alsó számjegyet elvet, ha ismert, hogy mindkét szám hiányával vagy mindkettővel felesleggel szedve; ha ez ismeretlen, akkor ezekben a számokban egy számjeggyel többet kell vennie, mint amennyit az eredményben szeretne szerepeltetni, és el kell dobnia az eredmény utolsó számjegyét.

195. Hozzávetőleges termék hibája. Az aritmetikai szorzás tulajdonságaiból tudjuk, hogy ha a két tényező valamelyike tetszőleges számmal csökken vagy nő, akkor a szorzat csökken vagy nő ezzel a számmal szorozva a másik tényezővel. Ezért, ha a két tényező közül az egyik pontos szám, a másik pedig hozzávetőleges, akkor a szorzat hibája egyenlő a közelítő tényező hibájával, szorozva a pontos tényezővel .

Példa. Számítsa ki 2πR, Hol π = 3,1415926... és R= 2,4 m.

A szám hozzávetőleges értékére korlátozva magát π 1/2 ezredig terjedő pontossággal (többlettel) kapjuk:

2πR = 3,142 4,8 = 15,0816.

A hiba kisebb, mint 1/2 4,8 = 2,4 ezredrész, és a közelítés több mint megfelelő lesz. Ha ennek eredményeként az utolsó két számjegyet elvetjük, azaz 16 tízezrelék = 1,6 ezrelék, az eredményt ugyanennyivel csökkentjük; ez azt jelenti, hogy a kapott 15,08-as szám pontosan 2,4-1,6 = 0,8 ezrelék lesz, ami kevesebb, mint 1 ezrelék (és ezért a 15,08-as eredmény jobban ábrázolható a következőképpen: 15,080); azonban továbbra sem ismert, hogy a 15,08-as közelítés többlettel vagy hiányossággal történik-e.

Ha mindkét tényező közelítő szám, a szorzat hibája a következőképpen határozható meg. Hadd A És b közelítések lesznek, mindkettőt hátrányosan veszik, és az első hibája az α , és a második β .
Majd pontos számok akarat egy + α És b + β . Találjuk meg a különbséget a pontos termék között ( egy + α ) (b + β ) és zárja be ab :

(egy + α ) (b +β ) - ab = ab + α b + A β + αβ - ab = α b + A β + αβ

A számok óta α És β kicsi, akkor a termék αβ olyan kicsi, hogy elhanyagolható (például ha α <0,001 и β < 0,001, то αβ < 0,000001). Тогда можно сказать, что погрешность приближенного произведения ab egyenlő α b + A β , azaz egyenlő az egyes közelítő tényezők hibájának egy másik tényezővel való szorzatának összege. Ha mindkét tényezőt túllépjük, akkor a pontos számok lesznek A - α És b - β és akkor

ab - (A - α ) (b - β ) = ab - ab + α b + A β - αβ = α b + β A - αβ ,

vagy még mindig figyelmen kívül hagyva a számot αβ ,

ab - (A - α ) (b - β ) = α b + β A ,

vagyis a közelítő összeg hibáját ugyanaz az összeg fejezi ki, mint amit korábban találtunk.

Alkalmazzuk ezt a következő példára:

√3 √2 = 1,73205 ... 1,41422 ...

Négy tizedesjegyre szorítkozva szorozzuk meg a közelítéseket egy hátránnyal, 0,0001 pontossággal:

1,7320 1,4142 = 2,44939440.

Mivel mindegyik vett közelítés kisebb, mint 2, így a talált közelítő szorzat hibája kisebb, mint 0,0001 2 + 0,0001 2, azaz kevesebb, mint 4 tízezrelék, és ez hátrányos lesz. Ha ebben a termékben elvetjük a 39440 számokat, akkor tovább csökkentjük a terméket 4 tízezreléknél kisebb számmal; akkor a 2,449 szorzatot kapjuk, pontosan 4 + 4 = 8 tízezrelékre, ami kevesebb, mint 10 tízezrelék = 1 ezrelék. Ez azt jelenti, hogy a 2,449 hozzávetőleges szorzata hiányos lesz, és pontossága 0,001.

Egy adott esetben, amikor a négyzetgyökök szorzásáról beszélünk, mint például a példánkban, a szorzatot egyszerűbben találhatjuk meg, így: figyelembe véve, hogy √3 √2 = √6, a közelítő négyzetgyököt kinyerjük. 6 a kívánt pontossággal. Tehát a gyökeret ezredrészekre véve ugyanazt a 2,419 számot kapjuk, amelyet fent más módon kaptunk.

196. Rövidített szorzás. Jelöljük meg a következő rövidített szorzási módszert is, amely lehetővé teszi a szorzat gyors megtalálását előre meghatározott pontossággal. Tegyük fel, hogy meg kell találnia a terméket 0,001-es pontossággal:

314,159265358... 74,632543926 ...

Először jelezzük, hogyan történik a rövidített szorzás, majd elmagyarázzuk, hogy miért.

A szorzó számjegyeit a szorzó alatt írjuk alá fordított sorrendben jobbról balra úgy, hogy egyszerű mértékegységeinek számjegye a szorzószámjegye alatt álljon, amely 100-szor kisebb egységeket fejez ki, mint az adott pontosságot kifejező számjegy egységei, azaz esetünkben a 6 százezredes számjegy alatt. :

Ezután megszorozzuk a szorzószámot a szorzó minden egyes számjegyével, anélkül, hogy odafigyelnénk a szorzó azon számjegyeire, amelyek a szorzó számjegyétől jobbra vannak, amellyel szorozunk. Ezeket a részműveket egymás alá írjuk úgy, hogy a jobb oldali első számok ugyanabban a függőleges oszlopban legyenek, majd összeadjuk őket. A kapott számban eldobjuk az utolsó két számjegyet, és a fennmaradó számjegyek közül az utolsót növeljük 1-gyel. Végül vesszőt teszünk úgy, hogy az utolsó számjegy a szükséges számjegy egységeit, azaz esetünkben ezredrészét fejezze ki. A kapott 23446.505 szám pontossága 0,001 (ismeretlen marad, alatta vagy felett).

Most magyarázzuk el ezt a rövidített szorzási technikát.

Mindenekelőtt győződjünk meg arról, hogy minden résztermék ugyanazon kategória egységeit fejezi ki, vagyis egy adott kategória 100-szor kisebb egységeit (példánkban százezrelék). Valóban, ha a 314159265 számot megszorozzuk az első 7-es számjegygel, a milliomodokat tízesekkel szorozzuk, ami azt jelenti, hogy százezreléket kapunk a szorzatban. Ezután a 31415926 számot megszorozzuk 4-gyel, a százezreléket megszorozzuk egyszerű egységekkel; Ez azt jelenti, hogy ismét százezreléket kapunk a szorzatban stb. Ebből az következik, hogy a 2344650499 összeg százezreléket fejez ki, azaz ez a 23446.50499 szám. Mutassuk meg, hogy a végeredmény hibája kisebb, mint 0,001.

Mivel a szorzónak a szorzó 7-es számától jobbra írt része kisebb, mint 1 milliomod, ezért ennek a résznek a szorzatát 70-nel figyelmen kívül hagyva 7 százezreléknél kisebb számmal csökkentjük az eredményt. Továbbá, mivel a szorzószámnak a szorzó 4-es számától jobbra írt része kisebb, mint 1 százezred, ezért ennek a résznek a szorzatát 4 egyszerű egységgel figyelmen kívül hagyva az eredményt 4 száznál kisebb számmal csökkentjük. ezredrészét. Hasonló módon érvelve a tényező összes többi számjegyére vonatkozóan, amellyel szoroznunk kell, megjegyezzük, hogy az eredményt 7 + 4 + 6 + + 3 + 2 + 5 + 4 + 3 + 9 száznál kisebb számmal csökkentjük. ezredrészét. Végül, mivel a szorzó kisebb, mint 1 ezer, és a szorzótól balra írt faktor része (amit tehát egyáltalán nem kell szorozni) kisebb, mint 2 + 1 százmilliomod, akkor figyelmen kívül hagyva a szorzószám szorzata a tényező ezen részével, tovább csökkentjük az eredményt 2 + 1 százezreléknél kisebb számmal. Ezért a pontos szorzat helyett a 23446.50499 számot véve az elsőt egy kisebb számmal csökkentjük, mint (7 + 4 + 6 + 3 + 2 + 5 + 4 + 3 + 9) + 2 +1 százezrelék, azaz általában kevesebb 101 százezreléknél, kivéve, ha a szorzási tényező számjegyeinek összege, növelve az eldobott számjegyei közül az elsővel, nem haladja meg a 100-at (ez mindig így van, ha a résztermékek száma nem haladja meg a 10). Ezenkívül az eredmény utolsó két számjegyének elvetésével ismét csökkentjük a szorzatot 99 százezreléket meg nem haladó számmal. Ezért a teljes csökkenés kisebb lesz, mint 101 + 99 százezred, azaz kevesebb, mint 2 ezrelék; ha az utolsó számjegyet 1-gyel, azaz 1 ezrelékkel növeljük, akkor a 23446.505 eredmény kevesebb, mint 2-1 ezrelékkel, azaz kevesebb mint egy ezrelékkel tér el a pontos szorzattól (és nem tudni, hogy többlettel vagy hiányossággal lesz-e) .

Vegye figyelembe, hogy nem mindig szükséges 1-gyel növelni a termék utolsó visszatartott számjegyét. Ezt a vizsgált példában meg kellett tenni, mert ott a szorzat hibája (mielőtt az utolsó számjegyét 1-gyel növeli) kisebb, mint az összeg

(7 + 4 + 6 +3 + 2 + 5 + 4 + 3+ 9) + 2 + 1 + 99 százezrelék = 145 százezrelék,

ami 100 és 200 százezrelék között van. De ha az eldobott 2 számjegy nem 99 lenne, hanem pl. 25, akkor a szorzat hibája kisebb lenne, mint az összeg

(7 + 4 + 6 +3 + 2 + 5 + 4 + 3+ 9) + 2 + 1 + 25 százezrelék = 71 százezrelék,

ami viszont kisebb, mint 100 százezrelék, azaz kevesebb, mint 1 ezrelék. Ez azt jelenti, hogy akkor nem kell az utolsó számjegyet 1-gyel növelni. Ebben az esetben a szorzat hátrányba kerülne.

Megjegyzés. A rövidített szorzás szabályának alkalmazásakor nem fordítunk figyelmet a szorzó azon számjegyeire, amelyek a szorzótól jobbra, és a szorzó azon számjegyeire, amelyek a szorzótól balra vannak; Mindkettőt teljesen elvethetjük. Így a szükséges számjegyek szorzójának és szorzójának ugyanazt a számot kell tartalmaznia; Nem nehéz előre meghatározni, hány számjegyből kell állnia ahhoz, hogy a termék adott pontossággal legyen. Magyarázzuk meg ezt egy példával. Tegyük fel, hogy ki kell számítanunk a szorzat 1/100-át

1000π (√5 - 1),

Ahol π a kerület és az átmérő aránya, egyenlő: 3,1415926535... Figyelve az utolsó szorzásra, így érvelünk: a szükséges szorzatot századrészre kell kiszámítani; ez azt jelenti, hogy a szorzó prímegységeinek számjegyének (azaz √5 - 1) a szorzószám negyedik tizedesjegye alatt kell szerepelnie; másrészt a szorzóban (√5 - 1) nincsenek egyszerűeknél magasabb számjegyek; ebből azt a következtetést vonjuk le, hogy a szorzóban több mint 4 tizedesjegy van, azaz 1000-ben π , hiába számolgatni. Ez 1000-et jelent π egyenlőnek kell lennie 3141,5926-tal; ezért a szorzóban, azaz √5 - 1-ben 8 számjegyet kell kiszámolni. Kivonással azt találjuk, hogy √5 =2,2360679, és ezért √5 -1 = 1,2360679. A művelet a következőképpen történik:

197. Egy közelítő hányados hibája. Ha az osztalék hozzávetőleges szám, az osztó pedig egy pontos szám, akkor a hányados hibája egyenlő a közelítő hibájának hányadosával osztva a pontos osztóval , a hozzávetőleges hányados pedig hiányos vagy többlettel lesz, attól függően, hogy a hozzávetőleges osztalékot hiánnyal vagy többlettel vesszük.

Például számítsuk ki a hányadost:

Három tizedesjegyre korlátozva az osztalékot, megszorozzuk:

0,538 7 = 3,766.

1/2-es hátrányos terméket kaptunk. 7 = 3 1/2 ezrelék, és ezért a 3,766: 3 = 1,25533... hányadosnak is hátránya lesz, és a hiba kisebb legyen, mint 3 1/2: 3 = 1 1/2 ezred. Ha a kapott hányadosban a századok számát követő számokat elvetjük, azaz csak 1,25-öt veszünk fel, akkor tovább csökkentjük a hányadost hat ezreléknél kisebb számmal; Ez azt jelenti, hogy az 1,25 szám hibája kisebb lesz, mint 6 +1 1/6 = 7 1/6 ezrelék, ami kevesebb, mint 10 ezrelék, azaz kevesebb, mint 1 század.

198. Rövidített felosztás. Ha az osztó hozzávetőleges szám, és az osztalék pontos vagy közelítő, akkor nehéz meghatározni a hányados hibahatárát. Ebben az esetben a legjobb a rövidített osztási módszert használni, amely lehetővé teszi, hogy viszonylag gyorsan megtalálja a hányadost előre meghatározott pontossággal.

A gyorsbillentyű megértéséhez először bizonyítjuk a következő segédigazságot: ha az osztó egy egész szám törttel, és ezt a törtet eltávolítjuk belőle, akkor a hányados kisebb számmal nő, mint ez a hányados osztva az osztó egész részével.

Legyen az osztalék A , osztó IN és az osztó tört része α . Ekkor az osztó egész része egyenlő IN - α és pontos hányados = A / B , közelítő hányados = A / B-α hányados növekedése =

Mert α < 1, то Aα < A ; ezért a magánélet növekedése< A / B : (IN - α ), azaz kisebb, mint az osztó egész részével elosztott hányados. Tegyük fel, hogy a hányadost 0,01-es pontossággal kell megtalálnunk:

31 415,92653... : 432,639...

Először jelezzük, hogyan történik a rövidített osztás, majd elmagyarázzuk, miért.

Nézzük meg, hány számjegynek kell lennie a közelítő hányadosban. Mivel az osztó nagyobb, mint az osztó szorozva 10-zel, de kisebb, mint az osztó szorozva 100-zal, ezért a hányados egész részének 2 számjegyűnek kell lennie. Mivel a hányadost századokra kell számítani, a hozzávetőleges hányados minden számjegyének 4-nek kell lennie.

Vegyük most ezt a 4-es számot, és adjunk hozzá annyi nullát, amennyit jelent; kapunk 40 ezret. Most válasszunk el annyi számjegyet a bal oldali osztóban (a vessző figyelmen kívül hagyásával), hogy 40 000-nél nagyobb (vagy azzal egyenlő) számot kapjunk; akkor az osztó 43 263 lesz. Az osztó maradék számjegyeit eldobjuk. Az osztalékban annyi számjegyet veszünk balra (a vesszőt figyelmen kívül hagyva), hogy az általuk képzett szám tartalmazza a rövidített osztót (legfeljebb 9-szer); akkor az osztalék 314 159 lesz. Az osztalék fennmaradó számjegyeit elvetjük.

Ezt az osztalékot elosztva az osztóval, megkapjuk a 7-es hányados első számjegyét és a 11,318 első maradékát. Ezután az osztóból kihúzunk egy 3-as jobboldali számjegyet, és a maradék 11318-at elosztjuk a 4326 osztó maradék számjegyeivel. megkapjuk a 2-es hányados második számjegyét, a második maradékot pedig 2666. Az osztóban még egy jobb oldali számjegyet, azaz 6-ot kihúzunk, a második maradékot pedig elosztjuk 432-vel. A 6-os hányados harmadik számjegyét és a harmadik számjegyét kapjuk maradék 74. Folytatjuk ezt a műveletet (minden hányadosnál áthúzunk egy számjegyet a jobb oldalon az osztóban), amíg az összes számjegyet priváttá nem kapjuk Végül a kapott hányadosba vesszőt teszünk úgy, hogy a jobb oldali utolsó számjegy a szükséges számjegy egységeit (példánkban a századokat) fejezze ki.

Most magyarázzuk el a rövidített felosztás folyamatát. Először is tegyük fel a kérdést, hogy a hányadost nem 0,01 pontossággal kell megtalálni, hanem egy egész szám egységnyi pontossággal, és az osztó egy 40 000-nél nem kisebb szám (vagyis az a szám, amelynek az első számjegye) és a nullák száma megegyezik a hányados számjegyeinek számával). Ehhez elegendő: 1) az osztalékot 100-szorosára növelni, ami ugyanennyivel növeli a hányadost, és ennek következtében a hibáját; 2) mozgassa a vesszőt az osztóban és az osztóban jobbra ugyanannyi számjegygel (ami nem változtatja meg a hányadost), csak annyira, hogy az osztó ne legyen kisebb, mint 40 000. Most a kérdés az egyhez pontos hányados:

314 159 265,3... : 43 203,9...

Hagyjuk el az osztó tört részét; ebből a fentebb bizonyítottnak megfelelően a hányadost egy kisebb számmal növeljük, mint ez a hányados osztva az osztó egész részével. De a hányados, amely a teljes részben 4 számjegyet tartalmaz, kisebb, mint 10 000, és az osztó teljes részét 40 000-nél nagyobbnak vettük; ez azt jelenti, hogy a hányadost 10 000-nél kisebb számmal növeljük: 40 000, azaz kevesebb, mint 1/4. Ezt szem előtt tartva megtaláljuk a hányadost:

314 159 265,3. . . : 43 263.

A hányados első számjegyének, azaz az ezresnek a megtalálásához el kell osztanunk az osztalék ezrei számát (314159) az osztóval. Ezt tettük a mi rövidített osztásunkban, megkaptuk a 7-es számot. A pontos osztalék maradéka 11 318 265,3 lesz... Ezt a maradékot el kell osztani 43 263-mal. Mindkét számot elosztjuk 10-zel 1131826,53 .. 4326,3. Ennek a hányadosnak csak 3 számjegye van az egész részében; ez azt jelenti, hogy kisebb, mint 1000. Az osztó törtjének elvetésével tovább növeljük a hányadost 1000-nél kisebb számmal: 4000, azaz kevesebb, mint 1/4; Ezt szem előtt tartva meg fogjuk találni a hányadost
1 131 826,53...: 4326. Ahhoz, hogy megtaláljuk ennek a hányadosnak az első számjegyét, azaz a százakat, el kell osztani az osztalék százainak számát (11 318) az osztóval (4320). Ezt tettük a rövidített felosztásunkban, és megkaptuk a hányados második számjegyét 2.

Mivel a hányadosban 4 számjegy van, ennek eredményeként a hányadost 1-nél kisebb mértékben növeljük. Másrészt anélkül, hogy a maradék 31-et elosztanánk a 43 utolsó osztójával, a hányadost 1-nél kisebb mértékben csökkentjük. Ez azt jelenti, hogy kevesebbel növeltük, mint 1-gyel, és kevesebbel csökkentettük. ezért az eredmény minden esetben 1-es pontosságú.

Már csak a vesszőt kell a megfelelő helyre tenni, 0,01-es pontossággal 72,61-et kapunk.

199. Megjegyzés. A fenti szabály és annak magyarázata nem igényel változtatást abban az esetben, ha valamelyik osztalék 10-szer tartalmazza a megfelelő osztót. Ezután a 10-es számot tesszük a hányadosba (zárójelbe). Az osztást folytatva azt látjuk, hogy a hányados minden következő számjegyének nullának kell lennie. Tegye például, hogy meg akarja találni a hányadost

485 172,923...: 78,254342...

pontos 1. A szabályt alkalmazva azt találjuk.

A harmadik osztalék (7823) tízszer tartalmazza a megfelelő osztót (782); a hányadosba a 10-et írjuk A hányados következő számjegye 0. A szükséges hányados a 61(10)0, azaz 6200.

Ebben az esetben a közelítő hányados nagyobb, mint a pontos hányados. Valójában a hányados számai, amelyeket még azelőtt találtunk, hogy ez a lehetőség felbukkant, nem lehetnek kisebbek a kelleténél, mivel minden hányadosra olyan osztókat vettünk, amelyek kisebbek a pontos osztónál. Ez azt jelenti, hogy a pontos hányados első két számjegyének 01-nél nem nagyobb számot kell kifejeznie, tehát kisebb, mint 6200.

Példa az előző szabályok alkalmazására a következő probléma.

200. Probléma. Számítsa ki a következő kifejezést 1/100 pontossággal:

Ez a kifejezés sajátos; ezért először is meghatározzuk, hogy hány számjegy legyen ebben a hányadosban, és ehhez ismernünk kell a legmagasabb számjegyét.
Miután elkezdtük a √348 és √127 kinyerését, látni fogjuk, hogy az első gyökér teljes részében 18-at, a második 11-et tartalmaz; ezért a számláló megközelítőleg 7, a nevező pedig megközelítőleg 2. Ez azt jelenti, hogy a hányadosban a legmagasabb rangot a prímegységek jelentik. Mivel a hányadost századokra kell számítani, ezért 3 számjegyűnek kell lennie. Ezért a nevezőt olyan pontosan kell kiszámítanunk, hogy lehessen (a rövidített osztás szabálya szerint) 3000-nél nagyobb számot képezni, amelyhez elegendő annak 5 számjegyét kiszámítani, és ehhez szükséges (a szabály szerint) a rövidített összeadásból), hogy megtaláljuk a 6 számjegyű nevező egyes gyökereit. A kibontás után a következőket találjuk:

√2 =1,41421; √3 = 1,73205; √5 =2,23606; √12 =3,46410, majd:

√2 + √3 + √5 - √12 =1,9183 (1/10000-ig).

Most olyan pontossággal kell kiszámolnunk a számlálót, hogy az első számjegyeiből 19183-nál nagyobb számot lehessen képezni. Mivel a számláló körülbelül 7, ezért az egész számon kívül még 4 tizedesjegyet kell kiszámítani. , és mivel a számláló különbség, akkor a minuendet és a részfejet is ki kell számítani a negyedik tizedesjegyig. A kibontással a következőket találjuk:

√348 =18,6547; √127 = 11,2694; √348 - √127 = 7,3853.

Marad a osztás a rövidített osztás szabálya szerint 73,853 p.1 19,183, ami után kapjuk:

x = 3,85 (1/100-ig)

Negyedik fejezet.

Irracionális kifejezések átalakítása.

201. Racionális és irracionális algebrai kifejezések. Egy algebrai kifejezést racionálisnak nevezünk a kifejezésben szereplő bármely betű vonatkozásában, ha ez a betű nem szerepel a gyökjel alatt; különben a kifejezést irracionálisnak nevezik ehhez a betűhöz képest. Például a kifejezés 3a +2 √x van benne valami racionális A és viszonylag irracionális X .

Ha azt mondják: „racionális (vagy irracionális) algebrai kifejezés”, anélkül, hogy melyik betűhöz hozzá kellene adni, akkor azt feltételezzük, hogy racionális (vagy irracionális) a kifejezésben szereplő összes betű tekintetében.

202. A radikális fő tulajdonsága. Vegye figyelembe, hogy a gyökök (gyökök), amelyekről ebben a fejezetben beszélünk, természetesen csak aritmetikaiak. Vegyünk például néhány radikálisat. 3 √ a , és emelje a gyökszámot valamilyen hatványra, például négyzetre; Ugyanakkor szorozzuk meg a gyök kitevőjét annak a foknak a kitevőjével, hogy milyen mértékben emeltük a gyökszámot, azaz esetünkben szorozzuk meg 2-vel. Ekkor kapunk egy új gyököt: 6 √ a 2 . Bizonyítsuk be, hogy ez a két művelet nem változtatta meg a gyök értékét.

Tegyük fel, hogy kiszámoltuk a 3 √-t a és kapott egy bizonyos számot X . Ekkor egyenlőségeket írhatunk:

X = 3 √a És x 3 = a .

Az utolsó egyenlőség mindkét oldalát négyzetre emelve a következőket kapjuk:

(x 3 ) 2 = a 2 , azaz x 6 = A 2 .

Az utolsó egyenlőségből világosan látszik, hogy X = 6 √a 2 .

Tehát ugyanaz a szám X egyenlő 3 √-val a , és 6 √ a 2 ezért:

3 √a = 6 √a 2 .

Hasonlóképpen ellenőrizheti, hogy:

Egyáltalán, a gyök értéke nem fog változni, ha a gyökkifejezést valamelyest emeljük, és egyúttal a gyökkitevőt megszorozzuk a gyökkifejezés emelési fokának indexével.

203. A gyökök néhány átalakulása.

A) A különböző fokú gyökök azonos mutatókra redukálhatók (ahogyan a különböző nevezőjű törtek is ugyanarra a nevezőre redukálhatók). Ehhez elegendő az összes gyök kitevőjének közös többszörösét (lehetőleg a legkisebbet) megkeresni, és mindegyik kitevőjét megszorozni a megfelelő járulékos tényezővel, ugyanakkor az egyes gyökkifejezéseket a megfelelő mértékben megemelni.

Példa.

√fejsze ; 3 √a 2 ; 6 √x

A gyökök legkisebb többszöröse 6; további tényezők lesznek: az első gyöknél 3, a másodiknál 2 és a harmadiknál 1. Ezután

b) Ha a gyökkifejezés olyan hatvány, amelynek kitevője közös faktorral rendelkezik a gyök kitevőjével, akkor mindkét kitevő csökkenthető ezzel a tényezővel.

Példák.

V) Ha egy gyökkifejezés több hatvány szorzata, amelyek kitevőinek a gyök kitevőjével azonos a közös tényező, akkor minden kitevő redukálható ezzel a tényezővel.

Példa.

204. Hasonló gyökök. Hasonló gyökök azok, amelyek ugyanazokkal a gyökkifejezésekkel és azonos gyökkitevőkkel rendelkeznek. Ilyenek például a kifejezések:

+3a 3 √xy És -5b 3 √xy

annak megállapításához, hogy ezek a gyökök hasonlóak-e egymáshoz, először egyszerűsíteni kell őket, azaz ha lehetséges:

1) távolítsa el a gyök jele alól azokat a tényezőket, amelyekből a gyökér kinyerhető (6. § 6. fejezet, 169. § a) pont);

2) mentesül a gyökök alatti törtek nevezőitől (6. §, 6. fejezet, 169. §, c);

3) csökkentse a gyök fokát úgy, hogy a gyök- és gyökszám mutatóit közös tényezőjükkel csökkenti, ha van ilyen.

Példák.

1) Gyökök 3 √ 8fejsze 3 és 6 √ 64a 2 y 12 hasonló lesz, ha leegyszerűsítjük őket:

3 √8fejsze 3 = 2x 3 √a ; 6 √64a 2 év 12 = 2y 2 6 √a 2 = 2y 2 3 √a

2) Három gyök hasonló lesz, ha megszabadulunk a radikálisok alatti nevezőktől:

205. Cselekvés az irracionális monomokra.

A) Összeadás és kivonás. Az irracionális monomiumok hozzáadásához vagy kivonásához kösse össze őket plusz vagy mínusz jelekkel, és ha megjelennek, csökkentse le a hasonló kifejezéseket.

Példák.

b) Szorzás. Korábban láttuk (6. §, 6. fejezet, 168. §), hogy a termék gyökerének kinyeréséhez elegendő azt minden tényezőből külön-külön kinyerni; ez éppen ellenkezőleg azt jelenti, Több azonos fokú gyök szorzásához elegendő a gyökszámokat megszorozni.

Így: ; 3 √x 3 √y = 3 √xy

√a √b √c = √abc

Ha különböző kitevőjű gyököket adunk meg a szorzáshoz, akkor először egy kitevőre redukálhatók.

Példák.

V) Ha vannak együtthatók a gyökök előtt, akkor azokat megszorozzuk.

Osztály. Tudjuk, hogy a drbbi gyökér kivonásához elegendő a számlálóból és a nevezőből külön kiemelni (6. §, 6. fejezet, 168. §, c); ez fordítva azt jelenti: azaz.,

Az azonos kitevővel rendelkező gyökök elkülönítéséhez elegendő a gyökszámukat elosztani. x = 6 √a Ebből egyértelmű, hogy

, és ezért.

Példa Összegezve a tényezőt 2x

a 3. fokú gyök jele alatt kapjuk: 206 Műveletek irracionális polinomokra

ugyanazok a szabályok szerint készülnek, mint a racionális polinomokra. Például: 207. Tört nevezőjének megszabadítása gyököktől.

A számítást elvégezhetjük közvetlenül ezzel a képlettel, vagy először racionálissá tehetjük a nevezőjét, amihez elegendő ennek a törtnek mindkét tagját megszorozni a √3 + √2 összeggel:

A (2) képlet kényelmesebb a számításhoz, mint az (1) képlet, egyrészt azért, mert csak 3 műveletet tartalmaz, és nem 4-et, mint az (1) képlet, másrészt azért, mert amikor egy számításban, ami szükségszerűen csak közelítő, az eredmény hibáját viszonylag egyszerűen meghatározza a (2) képlet. Tehát, ha a √3 és √2 fél ezrelék pontosságú, akkor kapjuk:

x = 1,732 + 1,414 = 3,146.

Ez az eredmény 1/2 + 1/2 ezred pontosságú, azaz 1/1000-ig.

Adjunk néhány egyszerű példát a nevezők négyzetgyököktől való megszabadítására.

1) . Szorozzuk meg a tört mindkét tagját √5-tel

Ha a gyökjel alatt egy egész összetett szám található, akkor néha célszerű prímtényezőkre bontani, hogy meghatározzuk, milyen tényezők hiányoznak belőle, hogy tökéletes négyzet legyen. Ekkor elegendő a tört mindkét tagját megszorozni csak a hiányzó tényezők szorzatának négyzetgyökével. Például:

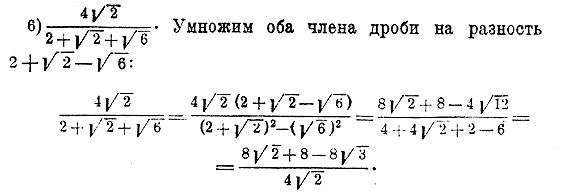
Ezután a tört mindkét tagját megszorozzuk √2-vel, így kapjuk:

______________

Racionális szám– egy m/n közönséges törttel ábrázolt szám, ahol az m számláló egész szám, az n nevező pedig egy természetes szám. Bármely racionális szám ábrázolható periodikus végtelen tizedes törtként. A racionális számok halmazát Q-val jelöljük.

Ha egy valós szám nem racionális, akkor az irracionális szám. Az irracionális számokat kifejező tizedes törtek végtelenek és nem periodikusak. Az irracionális számok halmazát általában nagy I betűvel jelöljük.

Valós számot hívnak algebrai, ha ez valamilyen racionális együtthatós polinom (nem nulla fokos) gyöke. Bármilyen nem algebrai számot hívunk transzcendentális.

Néhány tulajdonság:
A feladatok megoldása során célszerű az a + b√ c irracionális számmal együtt (ahol a, b racionális számok, c olyan egész szám, amely nem természetes szám négyzete) az a „konjugált” számot figyelembe venni. – b√ c: összege és szorzata az eredeti – racionális számokkal. Tehát a + b√ c és a – b√ c egy egész együtthatós másodfokú egyenlet gyöke.

Problémák a megoldásokkal

1. Bizonyítsd be

a) szám √ 7;

b) naplószám 80;

c) szám √ 2 + 3 √ 3;

irracionális.

a) Tegyük fel, hogy a √ 7 szám racionális. Ekkor van olyan p és q koprím, hogy √ 7 = p/q, innen kapjuk, hogy p 2 = 7q 2 . Mivel p és q viszonylag prím, akkor p 2, tehát p osztható 7-tel. Ekkor p = 7k, ahol k valamilyen természetes szám. Ezért q 2 = 7k 2 = pk, ami ellentmond annak, hogy p és q koprím.

Tehát a feltevés hamis, ami azt jelenti, hogy a √ 7 szám irracionális.

b) Tegyük fel, hogy a log 80 szám racionális. Ekkor van olyan természetes p és q, hogy log 80 = p/q, vagy 10 p = 80 q, amelyből 2 p–4q = 5 q–p értéket kapunk. Figyelembe véve, hogy a 2 és 5 számok viszonylag prímek, azt találjuk, hogy az utolsó egyenlőség csak p–4q = 0 és q–p = 0 esetén lehetséges. Innen p = q = 0, ami lehetetlen, mivel p és q van kiválasztva. hogy természetes legyen.

Tehát a feltevés hamis, ami azt jelenti, hogy az lg 80 szám irracionális.

c) Jelöljük ezt a számot x-szel.

Ekkor (x – √ 2) 3 = 3, vagy x 3 + 6x – 3 = √ 2 (3x 2 + 2). Az egyenlet négyzetre emelése után azt találjuk, hogy x-nek teljesítenie kell az egyenletet

x 6 – 6 x 4 – 6 x 3 + 12 x 2 – 36 x + 1 = 0.

Racionális gyökei csak az 1 és a –1 számok lehetnek. Az ellenőrzés azt mutatja, hogy 1 és –1 nem gyök.

Tehát a megadott √ 2 + 3 √ 3 szám irracionális.

2. Ismeretes, hogy az a, b, √a –√b,– racionális. Bizonyítsd be √a és √b racionális számok is.

Nézzük a munkát

(√ a – √ b)·(√ a + √ b) = a – b.

Szám √a +√b, amely egyenlő az a – b és számok arányával √a –√b, racionális, mivel két racionális szám hányadosa racionális szám. Két racionális szám összege

½ (√ a + √ b) + ½ (√ a – √ b) = √ a

– racionális szám, azok különbsége,

½ (√ a + √ b) – ½ (√ a – √ b) = √ b,

racionális szám is, amit bizonyítani kellett.

3. Bizonyítsuk be, hogy vannak olyan a és b pozitív irracionális számok, amelyeknél az a b szám természetes szám.

4. Vannak-e olyan a, b, c, d racionális számok, amelyek kielégítik az egyenlőséget?

(a + b √ 2 ) 2n + (c + d√ 2 ) 2n = 5 + 4√ 2 ,

ahol n természetes szám?

Ha a feltételben megadott egyenlőség teljesül, és az a, b, c, d számok racionálisak, akkor az egyenlőség is teljesül:

(a-b √ 2 ) 2n + (c – d√ 2 ) 2n = 5 – 4√ 2.

De 5 – 4√ 2 (a – b√ 2 ) 2n + (c – d√ 2 ) 2n > 0. A kapott ellentmondás azt bizonyítja, hogy az eredeti egyenlőség lehetetlen.

Válasz: nem léteznek.

5. Ha az a, b, c hosszúságú szakaszok háromszöget alkotnak, akkor minden n = 2, 3, 4, . . . az n √ a, n √ b, n √ c hosszúságú szakaszok is háromszöget alkotnak. Bizonyítsd be.

Ha a, b, c hosszúságú szakaszok háromszöget alkotnak, akkor a háromszög-egyenlőtlenség megadja

Ezért van

(n √ a + n √ b) n > a + b > c = (n √ c) n,

N √ a + n √ b > n √ c.

A háromszög-egyenlőtlenség ellenőrzésének fennmaradó eseteit hasonlóan vizsgáljuk, amiből a következtetés következik.

6. Bizonyítsuk be, hogy a 0,1234567891011121314... végtelen tizedes tört (a tizedesvessző után minden természetes számot sorrendben írunk) irracionális szám.

Mint tudják, a racionális számokat tizedes törtként fejezik ki, amelyeknek egy bizonyos előjellel kezdődő periódusuk van. Ezért elég bebizonyítani, hogy ez a tört egyetlen előjelben sem periodikus. Tegyük fel, hogy ez nem így van, és egy n számjegyű T sorozat a tört periódusa, amely az m-edik tizedesjegytől kezdődik. Jól látható, hogy az m-edik előjel utáni számjegyek között vannak nem nulla egyesek, ezért a T számjegyek sorozatában van egy nem nulla számjegy. Ez azt jelenti, hogy a tizedesvessző utáni m-edik számjegytől kezdve bármely n számjegy között van egy nem nulla számjegy. Ennek a törtnek a decimális jelölésének azonban tartalmaznia kell a 100...0 = 10 k szám decimális jelölését, ahol k > m és k > n. Nyilvánvaló, hogy ez a bejegyzés az m-edik számjegytől jobbra található, és több mint n nullát tartalmaz egy sorban. Így olyan ellentmondást kapunk, amely befejezi a bizonyítást.

7. Adott egy végtelen tizedes tört 0,a 1 a 2 ... . Bizonyítsuk be, hogy a decimális jelölésében szereplő számjegyek átrendezhetők úgy, hogy a kapott tört racionális számot fejezzen ki.

Emlékezzünk vissza, hogy egy tört akkor és csak akkor fejez ki racionális számot, ha az periodikus, egy bizonyos előjelből indulva. A 0-tól 9-ig terjedő számokat két osztályra osztjuk: az első osztályba azokat a számokat, amelyek az eredeti törtben véges sokszor szerepelnek, a második osztályba azokat, amelyek az eredeti törtben végtelen számú alkalommal. Kezdjük el kiírni a periodikus törtet, amelyet a számok átrendezésével kaphatunk az eredetiből. Először a nulla és a vessző után véletlenszerű sorrendben felírjuk az első osztályból származó összes számot - mindegyiket annyiszor, ahányszor az eredeti tört jelölésében szerepel. A rögzített első osztályú számjegyek a tizedesjegy törtrészében előzik meg a pontot. Ezután jegyezzük fel egyenként a második osztályból származó számokat valamilyen sorrendben. Ezt a kombinációt időszaknak nyilvánítjuk, és végtelen számú alkalommal megismételjük. Így kiírtuk a szükséges periodikus törtet, amely egy bizonyos racionális számot fejez ki.

8. Bizonyítsuk be, hogy minden végtelen tizedes törtben van egy tetszőleges hosszúságú tizedesjegyek sorozata, amely végtelen sokszor előfordul a tört felbontásában.

Legyen m egy tetszőlegesen megadott természetes szám. Osszuk ezt a végtelen tizedes törtet m számjegyű szegmensekre. Végtelen számú ilyen szegmens lesz. Másrészt mindössze 10 m különböző rendszer létezik, amelyek m számjegyből, azaz véges számból állnak. Következésképpen ezen rendszerek közül legalább egyet itt végtelenül sokszor meg kell ismételni.

Megjegyzés. Irracionális számok esetén √ 2, π vagy e még azt sem tudjuk, hogy melyik számjegy ismétlődik végtelenül sokszor az őket reprezentáló végtelen tizedes törtekben, bár ezekről a számokról könnyen bebizonyítható, hogy legalább két különböző ilyen számjegyet tartalmaznak.

9. Bizonyítsuk be elemi módon, hogy az egyenlet pozitív gyöke!

irracionális.

Ha x > 0, az egyenlet bal oldala növekszik x-szel, és könnyen belátható, hogy x = 1,5 esetén kisebb, mint 10, x = 1,6 esetén pedig nagyobb, mint 10. Ezért az egyetlen pozitív gyöke az egyenlet az (1,5 ; 1,6) intervallumon belül van.

Írjuk fel a gyököt p/q irreducibilis törtként, ahol p és q néhány viszonylag prím természetes szám. Ekkor x = p/q esetén az egyenlet a következő alakot veszi fel:

p 5 + pq 4 = 10q 5,

amiből az következik, hogy p osztója 10-nek, ezért p egyenlő az 1, 2, 5, 10 számok valamelyikével. Amikor azonban 1, 2, 5, 10 számlálóval írunk ki törteket, azonnal észrevesszük, hogy egyik sem esik az intervallumon belülre (1,5; 1,6).

Tehát az eredeti egyenlet pozitív gyöke nem ábrázolható közönséges törtként, ezért irracionális szám.

10. a) Van-e három olyan A, B és C pont a síkon, hogy bármely X pontra az XA, XB és XC szakaszok legalább egyikének hossza irracionális?

b) A háromszög csúcsainak koordinátái racionálisak. Bizonyítsuk be, hogy a körülírt kör középpontjának koordinátái is racionálisak.

c) Van-e olyan gömb, amelyen pontosan egy racionális pont van? (A racionális pont olyan pont, amelynek mindhárom derékszögű koordinátája racionális szám.)

a) Igen, léteznek. Legyen C az AB szakasz felezőpontja. Ekkor XC 2 = (2XA 2 + 2XB 2 – AB 2)/2. Ha az AB 2 szám irracionális, akkor az XA, XB és XC számok nem lehetnek egyszerre racionálisak.

b) Legyen (a 1 ; b 1), (a 2 ; b 2) és (a 3 ; b 3) a háromszög csúcsainak koordinátái. A körülírt kör középpontjának koordinátáit egy egyenletrendszer adja meg:

(x – a 1) 2 + (y – b 1) 2 = (x – a 2) 2 + (y – b 2) 2,

(x – a 1) 2 + (y – b 1) 2 = (x – a 3) 2 + (y – b 3) 2.

Könnyen ellenőrizhető, hogy ezek az egyenletek lineárisak, ami azt jelenti, hogy a vizsgált egyenletrendszer megoldása racionális.

c) Létezik ilyen gömb. Például egy gömb az egyenlettel

(x – √ 2 ) 2 + y 2 + z 2 = 2.

Az O pont koordinátákkal (0; 0; 0) egy racionális pont, amely ezen a gömbön fekszik. A gömb többi pontja irracionális. Bizonyítsuk be.

Tegyük fel az ellenkezőjét: legyen (x; y; z) a gömb racionális pontja, amely különbözik az O ponttól. Nyilvánvaló, hogy x különbözik 0-tól, mivel x = 0-nál van egy egyedi megoldás (0; 0; 0), amely most nem elérhető számunkra. Nyissuk ki a zárójeleket, és fejezzük ki a √ 2-t:

x 2 – 2√ 2 x + 2 + y 2 + z 2 = 2

√ 2 = (x 2 + y 2 + z 2)/(2x),

ami nem történhet meg racionális x, y, z és irracionális √ 2 esetén. Tehát O(0; 0; 0) az egyetlen racionális pont a vizsgált gömbön.

Problémák megoldások nélkül

1. Bizonyítsuk be, hogy a szám

\[ \sqrt(10+\sqrt(24)+\sqrt(40)+\sqrt(60)) \]

irracionális.

2. Milyen m és n egész számokra teljesül az (5 + 3√ 2 ) m = (3 + 5√ 2 ) n egyenlőség?

3. Van-e olyan a szám, amelyre az a – √ 3 és az 1/a + √ 3 számok egészek?

4. Az 1, √ 2, 4 számok lehetnek tagjai (nem feltétlenül szomszédosak) egy aritmetikai sorozatnak?

5. Bizonyítsuk be, hogy bármely n természetes számra az (x + y√ 3) 2n = 1 + √ 3 egyenletnek nincs megoldása racionális számokban (x; y).

Előző cikk: Mekkora a fénysebesség Következő cikk: Harmonikus rezgések Az oszcillációs frekvencia fizikai képlete

Hogyan lehet megszabadulni az irracionalitástól törtekben. Irracionális számok – Tudáshipermarket

Természetes számok $\mathbb(N)$

Egész számok $\mathbb(Z)$

Racionális számok $\mathbb(Q)$

Irracionális számok $\mathbb(I)$

Valós számok $\mathbb(R)$

Komplex számok$\mathbb(C)$

Enciklopédiai YouTube

Példák az irracionalitás bizonyítására

2 gyöke

Történet

Antikvitás

Problémák a megoldásokkal

Problémák megoldások nélkül