Mi a különbség a határozott és a határozatlan integrál között? Határozott integrálok számítása részenkénti integráció módszerével és a változó megváltoztatásának módszerével
Program kérdések.
1. Az antiderivatív és határozatlan integrál fogalma.
2. A határozatlan integrál tulajdonságai.
3. Alapintegrálok táblázata.
4. Határozatlan integrálok számítási módszerei.
5. Határozott integrál.
6. A határozott integrál geometriai alkalmazásai.
Tipikus példák megoldása .
Határozatlan integrál .
Integráció helyettesítési módszerrel (változócsere).
A határozatlan integrálban lévő változó cseréje kétféle helyettesítéssel történik:
1) x= j( t), Ahol t egy új változó, és j( t) – folyamatosan differenciálható függvény; Akkor
t= y( x), Ahol t– új változó; ebben az esetben:
8.1. példa. Integrál kiszámítása
Megoldás. Számítsuk ki ezt az integrált helyettesítési módszerrel.
Visszatérve a régi változóhoz, megtaláljuk és behelyettesítjük a talált kifejezést:
Válasz: 
8.2. példa. Integrál kiszámítása
Megoldás. Vezessünk be egy új változót, ez a helyettesítés az integrált a következő alakba hozza:

Válasz: ![]() .
.
Alkatrészenkénti integráció módja.
Hadd U=U(x)És V=V(x) – argumentumfüggvények x, amelynek folytonos származékai vannak. Ekkor lehetséges a részenkénti integráció:
∫UdV = UV - ∫VdU
Ahol V képlettel találjuk meg V = ò dV.
A részenkénti integrálási képlet lehetővé teszi az integrál számításának csökkentését ∫UdV az integrál kiszámításához ∫VdU.
Az alkatrészenkénti integráció képletének sikeressége a tényezők helyes megválasztásától függ UÉs dV az eredeti integrál integrandusában. Van két hasznos szabályokat ehhez a választáshoz:
1. ∫ alakú integrálok P(x)e kx dx , ∫ P(x)sinkxdx, ∫ P(x)coskxdx ,
Ahol P(x) – polinom, és k– egy bizonyos szám, a fenti képlettel számolva, ha tesszük P(x)=U.
2. ∫ alakú integrálok P(x)lnxdx, ∫ P(x)arcsinxdx,∫ P(x)arccosxdx,
∫ P(x)arctgxdx,∫ P(x)arcctgxdx, Ahol P(x)– polinom. Mindezekben az integrálokban És részenkénti integrálásakor olyan függvényt vesznek fel, amely szorzója P(x),és a munka P(x)dx = dV.
8.3. példa. Integrál kiszámítása
Megoldás. Az alkatrészenkénti integrálási képlet szerint a következőket kapjuk:
![]()
Válasz: ![]()
8.4. példa. Integrál kiszámítása
Megoldás. Alkatrészenként integrálva a következőket kapjuk:
=  =
=
Válasz: ![]() .
.
Racionális törtek integrálása
A racionális tört a forma töredéke Ahol P(x)És Q(x) – polinomok. Ha egy polinom foka K(x) magasabb, mint a polinom fokszáma R(x), akkor egy ilyen racionális törtet nevezünk helyes; V másképp a tört úgynevezett rossz.
Az I., II., III. és IV. típusú legegyszerűbb törteket racionális törteknek nevezzük a következő típus:
II. Ahol m– egész szám, nagyobb egynél.
III. Ahol másodfokú trinomikus x 2 + px+ q nincs
igazi gyökerek.
IV. ![]() Ahol n egynél nagyobb egész szám, és
Ahol n egynél nagyobb egész szám, és
x 2 + px + q nincsenek igazi gyökerei.
Bármely megfelelő racionális tört egyedileg ábrázolható a legegyszerűbb racionális törtek összegeként következő szabály:
1. Szüksége van egy nevezőre K(x) lineáris és négyzetes tényezők, amelynek nincsenek valódi gyökerei.
2. A törtet egyszerű törtek összegére kell bontani a következő módon:
– minden tényező ( x – a)k bomlás K(x) megfelel a tört kiterjesztésében az űrlap bővítésének
![]()
Ahol A– polinom gyöke K(x), A k– ennek a gyökérnek a sokasága; A 1 , A 2 , …, A k – számok (meghatározatlan együtthatók);
– minden bővítési tényező K(x) – a forma kifejezése
Ahol l– a polinom többszöröse a bővítésben K(x); B iÉs C i (én = 1, 2, …, l) bizonytalan együtthatók.
3. Az így kapott egyenlőséget le kell redukálni közös nevezőés miután megkapta a két tört egyenlőségét ugyanazok a nevezők, tegye egyenlővé a számlálókat.
4. Kétféleképpen lehet megkeresni bizonyos együtthatókat.
Első út. Nyissa ki a konzolokat, hozzon hasonló tagjaiés az együtthatókat egyenlővé tesszük egyenlő fokozatok x.
Második út. Zárójelek nyitása nélkül állítsa be az argumentumot x sok különböző jelentések, hány bizonytalan együttható van.
Mindkét esetben rendszereket kapunk lineáris egyenletek a bizonytalan együtthatók tekintetében, amelynek megoldása megkapja a kívánt bizonytalan együtthatók értékeit.
Megjegyzés. Egy nem megfelelő racionális tört integráljának megtalálásához először is el kell különíteni tőle a teljes részt, azaz. formában van jelen:
![]()
Ahol M(x) egy polinom, és egy megfelelő racionális tört.
8.5. példa. Integrál kiszámítása ![]()
Megoldás. A tört nevezőjének gyökerei vannak x= 2 és x= -5, és a következőképpen faktorizálható:
Képzeljük el az integrandust egyszerű törtek összegeként:
![]()
Adjunk jobb oldal egyenlőség a közös nevezővel:
![]()
A számlálókat egyenlítve a következőket kapjuk:
Esély A 1 és A 2 kétféleképpen is megtalálható.
Első út. Nyissuk meg az utolsó egyenlőség jobb oldalán lévő zárójeleket, és mutassunk be hasonló kifejezéseket:
Tegyük egyenlővé az együtthatókat azonos fokokon x:
x 1 3 = A 1 + A 2
x 0 8 = 5A 1 - 2A 2
Kapunk egy két egyenletrendszert két ismeretlennel:
 , melynek megoldása meg fogjuk találni A 1 = 2, A 2 = 1.
, melynek megoldása meg fogjuk találni A 1 = 2, A 2 = 1.
Ennélfogva,
![]()
Második út. Beállítunk bizonyos értékeket x(lehetőleg azok az értékek, amelyeknél a legegyszerűbb törtek nevezője nulla):
| x = 2 x = -5 | |
Így a szükséges integrál
Válasz: ![]()
8.6. példa. Integrál kiszámítása ![]()
Megoldás. Képzeljük el az integrandust egyszerű törtek összegeként. Lineáris szorzó (x+ 3) ennek a törtnek a nevezője megfelel az a történek a ( x– 2) 2 – a forma legegyszerűbb törteinek összege ![]()
Ezért ennek a frakciónak az egyszerűbb frakciókra való felosztása a következőképpen alakul:
![]()
Az egyenlőség jobb oldalát összeadva és a számlálókat egyenlővé tesszük, azt kapjuk
A bizonytalan együtthatók kiszámításához mindkét fenti módszert kombináljuk.
Először is állítsunk be bizonyos értékeket x:

Tegyük egyenlővé az együtthatókat x 2, megkapjuk
![]()
Tehát megtaláljuk a szükséges integrált:

![]()
Válasz: ![]()
![]()
8.7. példa. Integrál kiszámítása ![]()
Megoldás. Az integrand függvény hibás racionális tört, ezért ehhez ki kell választani az egész részt, el kell osztani a számlálót a nevezővel.
A differenciálszámításban olyan feladatokat vettek figyelembe, amelyek megoldásához egy adott függvény deriváltját kellett megtalálni. Számos esetben meg kell oldani az inverz problémát: adott deriválton keressük meg a differenciált függvényt. Az ilyen jellegű problémákat a szakaszban oldjuk meg matematikai elemzés, hívott integrálszámítás. Mód integrálszámítás Lehetővé teszi a lapos alakzatok területeinek, az ívek hosszának, a testek térfogatának kiszámításával kapcsolatos feladatok megoldását, valamint egyéb geometriai és fizikai problémákat.
1. példa Legyen a pont sebessége (v) a (t) időpontban egyenlő 2t-val. Keressünk egy kifejezést egy pont koordinátájára a (t) időpontban (a pont egyenes vonalban mozog).
Megoldás. Ismeretes, hogy v=\frac(dx)(dt) . óta ben ebben az esetben\frac(dx)(dt)=2t , akkor a probléma megoldását az x=t^2 függvények jelenthetik; x=t^2+3 stb.; V Általános nézet a feltett kérdésre a választ x=t^2+C formában írjuk le, ahol C tetszőleges állandó.
A fenti példából egyértelműen kiderül inverz probléma Megvan végtelen halmaz döntéseket. Egy bizonyos mozgástörvény eléréséhez ismerni kell például egy pont helyzetét a t=0 időpontban. Ha t=0-nál x=0, akkor 0=0+C, tehát C=0.
Egy pont elmozdulása egy idő alatt egyenlő (b^2+C)-(a^2+C)=b^2-a^2, és ezért nem függ C-től.
Antiderivatív funkció
1. definíció. Legyen adott az y=f(x) függvény valamilyen X intervallumon. Az y=F(x) függvényt meghívjuk antiderivatív f(x)-re ezen az intervallumon, ha minden x\-re X-ben
F"(x)=f(x).
Bevezették az „antiderivatív” kifejezést francia matematikus J. L. Lagrange (1736-1813).
A következő tétel lehetővé teszi, hogy egy adott függvény összes antideriváltjának megtalálását egy megtalálására redukáljuk.
1. tétel. Ha egy y=f(x) függvénynek van F(x) antideriváltja egy X intervallumon, akkor az összes F(x)+C alakú függvény antideriválta lesz hozzá ugyanazon az intervallumon. Fordítva, az y=f(x),\,x\in X függvény bármely \Phi(x) antiderivatívja ábrázolható \Phi(x)+C-ként, ahol F(x) az egyik antiderivatív függvény, és C egy tetszőleges állandó.
Bizonyíték. Az antiderivált definíciója szerint F"(x)=f(x). Figyelembe véve, hogy egy konstans deriváltja egyenlő nullával, a következőt kapjuk:
(F(x)+C)"=F"(x)+C"=F"(x)=f(x).
Ez azt jelenti, hogy az F(x)+C az y=f(x) antideriváltja az X intervallumon.
Most mutassuk meg, hogy ha az y=f(x) függvény adott az F intervallumon, és F(x) az egyik antideriváltja f(x)-nek, akkor bármely \Phi(x) antiderivált ábrázolható \Phi-ként. (x) = F(x)+C.
Valójában az antiderivált definíciója szerint a következőket kapjuk: \Phi"(x)=f(x) és F"(x)=f(x) . De két függvény, amelynek az X intervallumon egyenlő deriváltja van, csak konstans taggal különbözik. Ez azt jelenti, hogy \Phi(x)=F(x)+C, amit bizonyítani kellett.
A határozatlan és határozott integrálok definíciói
2. definíció. Az y=f(x) függvény összes antideriváltjának halmazát az X intervallumon nem nevezzük határozott integrál f(x) esetén, és jelöli.
Az y=f(x) függvényt meghívjuk integrand függvény Mert \textstyle(\int f(x)\,dx), és az f(x)\,dx szorzat - integrand.
És így, \int f(x)\,dx=\(F(x)+C\mid C\in \mathbb(R)\). A gyakorlatban egy rövidebb jelölés is elfogadott: \int f(x)\,dx=F(x)+C.
Gyakran mondják: „Vedd határozatlan integrál" vagy "számítsa ki a határozatlan integrált", ami a következőket jelenti: keresse meg az integrandus összes antideriváltjának halmazát.
Láttuk, hogy ha egy függvénynek legalább egy antideriváltja van, akkor végtelen sok antideriváltja van. A gyakorlatban gyakran meg kell keresni az antiderivatív értékeinek különbségét a b és a pontokban. Ez a különbség nem függ egy tetszőleges C állandó megválasztásától. Valóban, ha \Phi(x)=F(x)+C , akkor
\Pi(b)-\Phi(b)=(F(b)+C)-(F(a)+C)=F(b)-F(a).
Így, \Phi(b)-\Phi(b)=F(b)-F(a), amit bizonyítani kellett.
Mivel a b és a pontban lévő antiderivált érték különbsége nem attól függ, hogy melyik funkció antiderivatívája Ha y=f(x) választjuk, ezt a különbséget a függvény szegmens feletti határozott integráljának nevezzük.
Definíció 3. Legyen az y=f(x) függvény adott egy szakaszon, és legyen rajta egy y=F(x) antiderivált. Az F(b)-F(a) különbséget nevezzük határozott integrál f(x) függvényeket a szegmens fölé és jelöli \textstyle(\int\limits_(a)^(b)f(x)\,dx). Így,
\int\limits_(a)^(b)f(x)\,dx=F(b)-F(a).
Az F(b)-F(a) különbséget így írjuk fel \Bigl.(F(x))\Bigr|_(a)^(b), Akkor \textstyle(\int\limits_(a)^(b) f(x)\,dx= \Bigl.(F(x))\Bigr|_(a)^(b)). Az a és b számokat hívják az integráció határai.
Például az y=\frac(x^3)(3) az y=x^2 függvény egyik antideriváltja. Ezért
\int\limits_(a)^(b)x^2\,dx=\left.(\frac(x^3)(3))\right|_(a)^(b)=\frac(b^ 3)(3)-\frac(a^3)(3)=\frac(b^3-a^3)(3)\,.
Haladjunk tovább geometriai érzék bevezetett fogalmakat. Legyen F(x) az f(x) antideriváltja. Az y=F(x) függvény grafikonjának minden pontjában az érintő szögegyütthatója egyenlő F"(x), azaz f(x) értékkel. Ezért az antiderivált geometriai megtalálásának problémája a következőket jelenti: tudván lejtő minden pontban érintő, keresse meg a görbét. Mivel az ordináta tengely mentén történő párhuzamos transzláció során az érintő szögegyütthatója egy adott abszcissza pontban nem változik, így egy ilyen görbét találva abból kapjuk meg az összes többi szükséges görbét. párhuzamos átvitel az ordináta tengely irányába. Ez a görbecsalád (1. ábra) a határozatlan integrál geometriai illusztrációja.
Határozott integrál \textstyle(\int\limits_(a)^(b)f(x)\,dx=F(b)-F(a))ábra mutatja az y=F(x)+C görbék ordinátájának változását a pontból b pontba való mozgáskor. Mivel ezeket a görbéket az ordináta tengelyének irányába történő párhuzamos transzlációval kapjuk meg egymástól, az ordináta jelzett változása minden görbe esetében azonos (2. ábra).
Tekintsünk olyan problémákat, amelyek megoldása határozott integrálok kiszámításában merül ki.
1. feladat. Hagyja, hogy az M pont egy egyenes vonalban mozogjon, és legyen ismert ennek a pontnak a mozgási sebessége v=v(t) az intervallum bármely (x) időpontjában (t). Határozzuk meg az M pont elmozdulását (elmozdulásait) ez idő alatt.
Megoldás. Tudjuk, hogy ha x=x(t) egy pont mozgástörvénye, akkor v(t)=x"(t). Ezért x(t) a v=v(t) függvény egyik antideriváltja. ). a v=v(t) függvény antiderivált értékeinek különbségére, tehát b és a. s=\textstyle(\int\limits_(a)^(b)v(t)\,dt).
Tehát például egy test sebessége at szabadesés a v=gt képlettel kifejezve. Ebben az esetben a zuhanó test által az esés kezdetétől számított b másodperc alatt megtett utat a következőképpen számítjuk ki:
S=\int\limits_(0)^(b)gt\,dt= \left.(\frac(gt^2)(2) )\right|_(0)^(b)= \frac(gb^ 2)(2)\,.
2. feladat. Keressük meg a területet ívelt trapéz aA\,Bb , amelyet az x tengely korlátoz, az x=a és x=b egyenesek, valamint az y=f(x) folytonos függvény grafikonja, amely csak nem negatív értékeket vesz fel ezen a szakaszon (ábra. 3).

Mielőtt rátérne a probléma megoldására, vegye figyelembe, hogy itt használjuk vizuális ábrázolás a területről lapos alak(további részletek a terület meghatározásáról).
Megoldás. Jelöljük S(x) az aA\,Nx\,(a görbe vonalú trapéz területét Adjuk meg az x abszcisszának a \Delta x növekményt (a határozottsághoz tegyük \Delta x>0-t), ekkor a terület megkapja a \Delta S növekményt. Jelöljük m-rel az y=f(x) függvény legkisebb értékét a szegmensen, M-vel pedig ugyanazon függvény legnagyobb értékét ugyanazon a szakaszon. Akkor egyértelmű m\cdot\Delta x\leqslant\Delta S\leqslant M\cdot\Delta x, ami azt jelenti m\leqslant\frac(\Delta S)(\Delta x)\leqslant M. Ha \Delta x\to 0 , akkor az y=f(x) függvény folytonossága miatt lesz: \lim_(\Delta x\to0)m=\lim_(\Delta x\to0)=f(x). Ez azt jelenti, hogy van is \lim\frac(\Delta S)(\Delta x), és ez a határ egyenlő f(x) -vel. Így S"(x)=f(x) . A kapott egyenlőség azt jelenti, hogy S(x) az y=f(x) függvény egyik antideriváltja. Mivel az x=a egyenes „levág” egy nulla területű alakot az aABb trapézból, akkor S(a)=0. Másrészt S(b) a teljes aABb görbe trapéz területe. Ez azt jelenti, hogy a szükséges S terület egyenlő (S(b)-S(a)), azaz. egyenlő az y=f(x) függvény egyik antiderivált értékei közötti különbséggel a b és a pontokban. Ez azt jelenti \boldsymbol(S=\int\limits_(a)^(b)f(x)\,dx\,.) 2. példa Határozzuk meg az ábra x tengely és egy félhullám szinuszos y=\sin(x) által határolt területét (4. ábra). Megoldás. A szükséges S területet a képlet fejezi ki \textstyle(S= \int\limits_(0)^(\pi)\sin(x)\,dx). Az y=\sin(x) függvény egyik antideriváltja a (-\cos(x)), mivel (-\cos(x))"=\sin(x)). Eszközök, S= \int\limits_(0)^(\pi)\sin(x)\,dx=\Bigl.(-\cos(x))\Bigr|_(0)^(\pi)= -(\ cos\pi-\cos0)=-(-1-1)=2. Ennek a szakasznak a befejezéseként nézzük meg a határozatlan integrál két olyan tulajdonságát, amelyek könnyen megkaphatók a definícióból. 1°. A határozatlan integrál differenciálja egyenlő az integrandusszal, a határozatlan integrál deriváltja pedig egyenlő az integrandusszal: D\!\left(\int f(x)\,dx\right)= f(x)\,dx,\quad \left(\int f(x)\,dx\jobb)"=f(x) . Bizonyíték. Mert \textstyle(\int f(x)\,dx=F(x)+C), ahol F"(x)=f(x) , akkor \textstyle(\left(\int f(x)\,dx\right)"= \bigl(F(x)+C\bigr)"=F"(x)+C"=f(x)). De aztán \textstyle(d\!\left(\int f(x)\,dx\right)= \left(\int f(x)\,dx\right)"dx=f(x)\,dx). Ezt az állítást gyakran használják az integráció eredményének ellenőrzésére. Hadd például ezt meg kell mutatnod \int5x\,dx=\frac(5)(2)\,x^2+C\quad (C=\text(const)). Differenciálva az egyenlőség jobb oldalát, megkapjuk az integrandust: \left(\frac(5)(2)\,x^2+C\right)"=\frac(5)(2)\cdot 2x+0=5x. Eszközök, \int5x\,dx=\frac(5)(2)\,x^2+C. 2°. Valamely függvény deriváltjának határozatlan integrálja egyenlő ezzel a függvénnyel egy tetszőleges állandóhoz hozzáadva: \int F"(x)\,dx=F(x)+C. Bizonyíték. Mert \bigl(F(x)+C\bigr)"=F"(x), akkor a határozatlan integrál definíciója szerint \textstyle(\int F"(x)\,dx=F(x)+C), amit bizonyítani kellett. Tekintve, hogy F"(x)\,dx=d\bigl(F(x)\bigr), a 2° tulajdonság a következőképpen is felírható: \textstyle(\int d\bigl(F(x)\bigr)=F(x)+C). Az előző bekezdésben szereplő 1° tulajdonság használatával a derivált táblázat segítségével létrehozhat egy táblázatot az alapvető integrálokról. Például azóta (\sin(x))"=\cos(x), Azt \int\cos(x)\,dx=\sin(x)+C.. Bizonyítsuk be \int\dfrac(1)(x)\,dx=\ln|x|+C. Valóban, ha x>0, akkor |x|=x, és ezért \bigl(\ln|x|\bigr)"=\bigl(\ln(x)\bigr)"=\frac(1)(x)\,. Ha x<0
, то |x|=-x
и, следовательно, \bigl(\ln|x|\bigr)"=\bigl(\ln(-x)\bigr)"= \frac(1)(-x)\cdot(-1)=\frac(1)(x ). Így, \bigl(\ln|x|\bigr)"=\frac(1)(x), ami azt jelenti \int\frac(1)(x)\,dx=\ln|x|+C. Ez a képlet alkalmazható a nyitott sugárra (0;+\infty) vagy a nyitott sugárra (-\infty;0) . Alapintegrálok táblázata \begin(aligned)&\boldsymbol(1.)\quad \int 0\,dx=C; &\quad &\boldsymbol(2.)\quad \int 1\,dx=\int dx=x+C;\\ &\boldsymbol(3.)\quad \int x^(a)\,dx=\ frac(x^(a+1))(a+1)+C,~a\ne-1; &\quad &\boldsymbol(4.)\quad \int \frac(dx)(x)=\ln(x)+C;\\ &\boldsymbol(5.)\quad \int \frac(dx)( a^2+x^2)=\frac(1)(a)\operátornév(arctg)\frac(x)(a)+C; &\quad &\boldsymbol(6.)\quad \int \frac(dx)(\sqrt(a^2-x^2))=\arcsin\frac(x)(a)+C;\\ &\ félkövér szimbólum(7.)\quad \int a^x\,dx=\frac(a^x)(\ln a)+C; &\quad &\boldsymbol(8.)\quad \int e^x\,dx=e^x+C;\\ &\boldsymbol(9.)\quad \int \sin(x)\,dx=- \cos(x)+C; &\quad &\boldsymbol(10.)\quad \int \cos(x)\,dx=\sin(x)+C;\\ &\boldsymbol(11.)\quad \int \frac(dx)( \sin^2x)=-\operátornév(ctg)x+C; &\quad &\boldsymbol(12.)\quad \int \frac(dx)(\cos^2x)=\operátornév(tg)x+C;\\ &\boldsymbol(13.)\quad \int \frac (dx)(x^2-a^2)=\frac(1)(2a)\ln\! \left|\frac(x-a)(x+a)\right|+C; &\quad &\boldsymbol(14.)\quad \int \frac(dx)(\sqrt(x^2\pm a^2))=\ln \bigl|x+\sqrt(x^2\pm a^ 2)\bigr|+C.\\ \end(igazított) Vegye figyelembe, hogy az ezekben a képletekben szereplő x változó bármely mással helyettesíthető. Például a képlet helyett \textstyle(\int\cos(x)\,dx= \sin(x)+C) tudsz írni \textstyle(\int\cos(t)\,dt= \sin(t)+C) stb. 3. példa Számítsuk ki a különböző törtek határozatlan integráljait: \mathsf(1))~\int\frac(dx)(\sqrt(x))\,;\quad \mathsf(2))~\int\frac(dx)(x^2+16)\,; \quad \mathsf(3))~\int\frac(dx)(x^2-16)\,;\quad \mathsf(4))~\int\frac(dx)(\sqrt(3-x^) 2))\,;\quad \mathsf(5))~\int\frac(dx)(\sqrt(x^2-3))\,. Megoldás. 1) Használjuk a 3. képletet az integrálok táblázatából: \int\frac(dx)(\sqrt(x))= \int x^(-1/3)\,dx= \frac(x^(-1/3+1))(-1/3+1 )+C= \frac(3)(2)\,x^(2/3)+C; 2) Használjuk az 5-ös képletet: \int\frac(dx)(x^2+16)= \int\frac(dx)(x^2+4^2)=\frac(1)(4) \operátornév(arctg)\frac(x) (2)+C;. 3) Használjuk a 12-es képletet: \int\frac(dx)(x^2-16)= \int\frac(dx)(x^2-4^2)= \frac(1)(8)\ln\!\left|\frac( x-4)(x+4)\jobbra|+C;. 4) Használjuk a 6-os képletet: \int\frac(dx)(\sqrt(3-x^2))= \int\frac(dx)(\sqrt((\sqrt(3))^2-x^2))= \arcsin\frac (x)(\sqrt(3))+C;. 5) Használjuk a 13-as képletet: \int\frac(dx)(\sqrt(x^2-3))= \ln\Bigl|x+\sqrt(x^2-3)\Bigr|+C.. Határozott integrállal
folytonos függvényből f(x) az utolsó szegmensben [ a, b] (ahol ) néhány antiderivált növekménye ezen a szegmensen. (Általában a megértés észrevehetően könnyebb lesz, ha megismétli a határozatlan integrál témakörét) Ebben az esetben a jelölést használjuk Amint az az alábbi grafikonokon látható (az antiderivatív függvény növekedését jelöli), egy határozott integrál lehet pozitív vagy negatív szám(Az antiderivatív felső határértéke és alsó határértéke közötti különbségként számítják ki, azaz pl. F(b) - F(a)). Számok aÉs b az integráció alsó és felső határának, illetve a szegmens [ a, b] – az integráció szegmense. Így ha F(x) – valamilyen antiderivatív funkció a f(x), akkor a definíció szerint Az egyenlőséget (38) nevezzük Newton-Leibniz képlet
. Különbség F(b) – F(a) röviden a következőképpen van leírva: Ezért a Newton-Leibniz képletet így írjuk: Bizonyítsuk be, hogy a határozott integrál nem függ attól, hogy az integrandus melyik antideriváltját veszi számítása során. Hadd F(x) és F( x) az integrandus tetszőleges antideriváltjai. Mivel ezek azonos funkciójú antideriválták, egy állandó taggal különböznek egymástól: Ф( x) = F(x) + C. Ezért Ez megállapítja, hogy a szegmensen [ a, b] a függvény összes antiderivált növekménye f(x) egyeznek meg. Így egy határozott integrál kiszámításához meg kell találni az integrandus bármely antideriváltját, azaz. Először meg kell találnia a határozatlan integrált. Állandó VAL VEL
kizárják a későbbi számításokból. Ezután a Newton-Leibniz képletet alkalmazzuk: a felső határ értékét behelyettesítjük az antiderivatív függvénybe b
, tovább - az alsó határ értéke a
és kiszámolják a különbséget F(b) - F(a)
. A kapott szám egy határozott integrál lesz.. Nál nél a = bértelemszerűen elfogadott 1. példa Megoldás. Először keressük meg a határozatlan integrált: A Newton-Leibniz képlet alkalmazása az antiderivátumra (nál nél VAL VEL= 0), kapjuk Határozott integrál számításakor azonban jobb, ha nem külön keressük meg az antideriváltat, hanem azonnal írjuk az integrált a (39) alakba. 2. példa Határozott integrál kiszámítása Megoldás. Képlet segítségével 2. tétel.A határozott integrál értéke nem függ az integrációs változó megnevezésétől, azaz Hadd F(x) – antiderivatív for f(x). Mert f(t) az antiderivált ugyanaz a funkciója F(t), amelyben a független változó csak másképp van megjelölve. Ennélfogva, A (39) képlet alapján az utolsó egyenlőség az integrálok egyenlőségét jelenti 3. tétel.A konstans tényező kivehető a határozott integrál előjeléből, azaz 4. tétel.Véges számú függvény algebrai összegének határozott integrálja egyenlő ezen függvények határozott integráljainak algebrai összegével, azaz 5. tétel.Ha az integráció egy szegmense részekre van osztva, akkor a teljes szegmensre vonatkozó határozott integrál egyenlő a részein lévő határozott integrálok összegével, azaz Ha 6. tétel.Az integrálási határok átrendezésekor a határozott integrál abszolút értéke nem változik, csak az előjele változik, azaz 7. tétel(átlagérték tétel). Egy határozott integrál egyenlő az integrációs szegmens hosszának és az integrandus értékének szorzatával egy bizonyos ponton belül, azaz 8. tétel.Ha az integráció felső határa nagyobb, mint az alsó, és az integrandus nem negatív (pozitív), akkor a határozott integrál is nem negatív (pozitív), azaz. Ha 9. tétel.Ha az integráció felső határa nagyobb, mint az alsó és a függvények és folytonosak, akkor az egyenlőtlenség terminusonként integrálható, azaz A határozott integrál tulajdonságai lehetővé teszik az integrálok közvetlen számításának egyszerűsítését. 5. példa Határozott integrál kiszámítása A 4. és 3. tétel felhasználásával és az antideriválták – a (7) és (6) táblaintegrálok – keresésekor megkapjuk Hadd f(x) – folyamatos a szegmensen [ a, b] függvény, és F(x) az antideriváltja. Tekintsük a határozott integrált és azon keresztül t az integrációs változót úgy jelöljük ki, hogy ne keverjük össze a felső korláttal. Amikor megváltozik x a határozott integrál (47) is változik, azaz. az integráció felső határának függvénye x, amivel jelöljük F(x), azaz Bizonyítsuk be, hogy a függvény F(x) egy antiderivatív a f(x) = f(t). Valóban, megkülönböztetés F(x), kapunk mert F(x) – antiderivatív for f(x), A F(a) egy állandó érték. Funkció F(x) – a végtelen számú antiderivatív egyike a f(x), nevezetesen azt, amelyik x = a nullára megy. Ezt az állítást kapjuk, ha a (48) egyenlőségbe tesszük x = aés használja az előző bekezdés 1. tételét. ahol definíció szerint F(x) – antiderivatív for f(x). Ha megváltoztatjuk a változót az integrandusban akkor a (16) képletnek megfelelően felírhatjuk Ebben a kifejezésben antiderivatív funkciója számára Valójában a származéka szerint összetett függvények differenciálási szabálya, egyenlő Legyen α és β a változó értéke t, amelyhez a függvény ennek megfelelően értékeket vesz fel aÉs b, azaz De a Newton-Leibniz képlet szerint a különbség F(b) – F(a) Van Az integrálok megoldása könnyű feladat, de csak néhány kiválasztott számára. Ez a cikk azoknak szól, akik szeretnének megtanulni megérteni az integrálokat, de semmit vagy szinte semmit nem tudnak róluk. Integrál... Miért van szükség rá? Hogyan kell kiszámolni? Mik azok a határozott és határozatlan integrálok? Ha az integrálnak csak egy horgolótűjét ismeri, amely egy integrál ikon alakú horgolótűt használ, hogy valami hasznosat hozzon ki a nehezen elérhető helyekről, akkor üdvözöljük! Tudja meg, hogyan kell megoldani az integrálokat, és miért nem megy nélküle. Az integráció már az ókori Egyiptomban ismert volt. Persze nem a modern formájában, de mégis. Azóta a matematikusok sok könyvet írtak erről a témáról. Különösen kitüntették magukat Newton
És Leibniz
, de a dolgok lényege nem változott. Hogyan lehet a semmiből megérteni az integrálokat? Semmiképpen! A téma megértéséhez továbbra is szüksége lesz a matematikai elemzés alapjainak alapismeretére. Az integrálok megértéséhez szükséges információk már vannak a blogunkon. Legyen valami funkciónk f(x)
. Határozatlan integrálfüggvény f(x)
ezt a függvényt hívják F(x)
, amelynek deriváltja egyenlő a függvénnyel f(x)
. Más szavakkal, az integrál egy fordított származék vagy egy antiderivált. A hogyanról egyébként cikkünkben olvashat. Minden folytonos funkcióhoz létezik antiderivált. Emellett gyakran konstans előjelet adnak az antideriválthoz, mivel a konstansban eltérő függvények származékai egybeesnek. Az integrál megtalálásának folyamatát integrációnak nevezzük. Egyszerű példa:
Annak érdekében, hogy ne számítsuk ki folyamatosan az elemi függvények antideriváltjait, célszerű táblázatba helyezni és kész értékeket használni: Amikor az integrál fogalmával foglalkozunk, végtelenül kicsi mennyiségekkel van dolgunk. Az integrál segít kiszámítani egy ábra területét, egy nem egyenletes test tömegét, az egyenetlen mozgás során megtett távolságot és még sok mást. Emlékeztetni kell arra, hogy az integrál végtelenül sok végtelenül kicsi tag összege. Példaként képzeljük el valamilyen függvény grafikonját. Hogyan találjuk meg egy függvény grafikonja által határolt ábra területét? Integrál használatával! A függvény koordinátatengelyei és grafikonja által határolt görbe vonalú trapézt osszuk fel infinitezimális szegmensekre. Így az ábra vékony oszlopokra lesz osztva. Az oszlopok területének összege a trapéz területe lesz. De ne feledje, hogy egy ilyen számítás hozzávetőleges eredményt ad. Azonban minél kisebbek és keskenyebbek a szegmensek, annál pontosabb lesz a számítás. Ha olyan mértékben csökkentjük őket, hogy a hosszúság nullára hajlik, akkor a szegmensek területének összege az ábra területéhez fog fordulni. Ez egy határozott integrál, amely így van írva: Apropó! Olvasóink most 10% kedvezményt kapnak Hogyan lehet megoldani egy határozatlan integrált? Itt megnézzük a határozatlan integrál tulajdonságait, ami a példák megoldásánál lesz hasznos. Azt már megtudtuk, hogy a határozott integrál egy összeg határa. De hogyan lehet konkrét értéket kapni egy példa megoldása során? Erre van a Newton-Leibniz képlet: Az alábbiakban néhány példát fogunk megvizsgálni a határozatlan integrálok megtalálására. Javasoljuk, hogy saját maga találja ki a megoldás bonyolultságát, és ha valami nem világos, tegye fel kérdéseit a megjegyzésekben. Az anyag megerősítéséhez nézzen meg egy videót az integrálok gyakorlati megoldásáról. Ne essen kétségbe, ha az integrált nem adják meg azonnal. Forduljon egy professzionális diákszolgálathoz, és minden zárt felületen lévő hármas vagy ívelt integrált az Ön rendelkezésére áll.

Alapintegrálok táblázata
A számítások elvégzéséhez engedélyezni kell az ActiveX-vezérlőket!

![]() (38)
(38)![]() (39)
(39)
![]()
![]()
![]()
A határozott integrál tulajdonságai
![]() (40)
(40)![]()
![]() (41)
(41)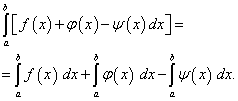 (42)
(42)![]() (43)
(43)![]() (44)
(44)![]() (45)
(45)
![]() (46)
(46)![]()

Határozott integrál változó felső határértékkel
![]() (47)
(47)![]() (48)
(48)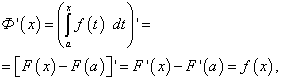
Határozott integrálok számítása részenkénti integráció módszerével és a változó megváltoztatásának módszerével
![]()


Tanulmányozzuk az "integrál" fogalmát
Határozatlan integrál



Határozott integrál


Az a és b pontokat integrációs határoknak nevezzük. Bari Alibasov és az "Integral" csoport
Bari Alibasov és az "Integral" csoport A próbabábu integrálszámításának szabályai
A határozatlan integrál tulajdonságai


Határozott integrál tulajdonságai




Példák integrálok megoldására

Előző cikk: Mekkora a fénysebesség
Következő cikk: Harmonikus rezgések Az oszcillációs frekvencia fizikai képlete
