Hogyan találjuk meg az egyenesek közötti szöget a koordináta módszerrel. Szög két egymást metsző sík között - meghatározás, példák a megtalálásra

Probléma 1.6. Adott kocka. M, N, P - az élek felezőpontja, AB, BC, ill. Keresse meg a síkok közötti szöget (MNP) és

a) Vezessünk be egy derékszögű derékszögű koordináta-rendszert a 17. ábrán látható módon. A kocka élének hossza tetszőlegesen megválasztható, hiszen homotéta esetén a síkok közötti szög nagysága nem változik. Kényelmes például egy kocka élének hosszát 2-vel egyenlőnek venni.

A kiválasztott koordinátarendszerhez viszonyítva megtaláljuk a pontok és vektorok koordinátáit:

b) Legyen a sík normálvektora.

Ebben az esetben a feltételek teljesülnek

Hasonlóképpen, ha a sík normálvektora, akkor

c) Ha, akkor

Válasz:

Probléma 1.7. A helyes alján háromszög alakú piramis A SABC helyes oldala egyenlő 2-vel. SA él merőleges az alap síkjára és SA = 1. A P, Q pontok az SB, NE élek felezőpontjai. A sík párhuzamos az SC és AB egyenesekkel, a sík pedig párhuzamos az AQ és CP egyenesekkel. Határozza meg a és a síkok közötti szög nagyságát!

a) Válasszunk egy derékszögű derékszögű koordinátarendszert a 18. ábrán látható módon. A kiválasztott koordinátarendszerben:

b) az SC és AB egyenesekkel párhuzamos sík normálvektora. akkor a feltételek teljesülnek:

c) Jelöljük az AQ és CP egyenesekkel párhuzamos síkkal és annak normálvektorával. Ebben az esetben egy formarendszert kapunk

Célok:

• fejlessze a problémamegoldás különböző megközelítéseinek mérlegelésének képességét és e megoldási módszerek alkalmazásának „hatásainak” elemzését;
• fejleszti a hallgató képességét, hogy matematikai preferenciáinak megfelelően válasszon módszert a probléma megoldására, szilárdabb tudás és magabiztos készségek alapján;
• fejleszteni kell az egymást követő szakaszokból álló terv összeállításának képességét az eredmények elérése érdekében;
• fejleszteni kell az összes lépés és számítás igazolásának képességét;
• ismételje meg és erősítse meg különféle témákat valamint a sztereometria és planimetria kérdései, az aktuális problémák megoldásához kapcsolódó tipikus sztereometrikus struktúrák;
• fejleszteni a térbeli gondolkodást.

• elemzés különféle módszerek feladatmegoldás: koordinátavektor módszer, koszinusztétel alkalmazása, három merőleges tételének alkalmazása;
• az egyes módszerek előnyeinek és hátrányainak összehasonlítása;
• kocka, háromszög prizma, szabályos hatszög tulajdonságainak ismétlése;
• felkészülés letette az egységes államvizsgát;
• a függetlenség fejlesztése a döntéshozatalban.

Óravázlat

Kocka alakú ABCDA 1 B 1 C 1 D 1éllel 1 pont O – homlokközép ABCD.

a) az egyenesek közötti szög A 1 DÉs B.O.;

b) távolság a ponttól B a szegmens közepéig A 1 D.

Az a) pont megoldása

Helyezzük el a kockánkat az ábrán látható téglalap alakú koordinátarendszerbe, a csúcsokba A1 (1; 0; 1), D (1; 1; 0), B1 (0; 0; 1), O (½; ½; 0).

Egyenesek irányvektorai A 1 DÉs B 1 O:

(0; 1; -1) és (½; ½; -1);

megkeressük köztük a kívánt φ szöget a képlet segítségével:

cos∠φ = ,
ahonnan ∠φ = 30°.

2. módszer. A koszinusz tételt használjuk.

1) Rajzoljunk egy egyenest B 1 C párhuzamos a vonallal A 1 D. Sarok CB 1 O az lesz, amit keresel.

2) Derékszögű háromszögből BB 1 O a Pitagorasz-tétel szerint:

3) Háromszögből származó koszinusztétel alapján CB 1 O kiszámítja a szöget CB 1 O:

cos CB 1 O = , a szükséges szög 30°.

Megjegyzés. A feladat 2. módon történő megoldása során észrevehető, hogy a három merőleges tétele szerint COB 1 = 90°, ezért téglalap ∆-ből CB 1 O Könnyen kiszámítható a kívánt szög koszinusza is.

A b) pont megoldása

1 út. Használjuk a két pont távolságának képletét

Legyen a lényeg E– középső A 1 D, majd a koordinátákat E (1; 1/2; 1/2), B (0; 0; 0).

BE = .

2. módszer. A Pitagorasz-tétel szerint

Téglalap ∆-ből B.A.E. közvetlennel B.A.E. találunk LENNI = .

Jobbra háromszög prizma ABCA 1 B 1 C 1 minden él egyenlő a. Keresse meg a vonalak közötti szöget ABÉs A 1 C.

1 út. Koordinátavektor módszer

A prizma csúcsainak koordinátái téglalap alakú rendszerben, ha a prizma az ábrán látható módon van elhelyezve: A (0; 0; 0), B (a; ; 0), A1 (0; 0; a), C (0; a; 0).

Egyenesek irányvektorai A 1 CÉs AB:

(0; a; -a)És (a; ; 0} ;

cos φ = ;

2. módszer. A koszinusz tételt használjuk

∆-t tekintjük A 1 B 1 C, amiben A 1 B 1 || AB. Nekünk van

cos φ = .

(Egységes államvizsga-2012 gyűjteményből. Matematika: jellemző vizsgalehetőségek szerkesztette A. L. Semenova, I. V. Jascsenko)

Jobbra hatszögletű prizma ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, amelynek minden éle egyenlő 1-gyel, keresse meg a pont távolságát E egyenesre B 1 C 1.

1 út. Koordinátavektor módszer

1) Helyezze el a prizmát egy téglalap alakú koordinátarendszerbe, a koordinátatengelyeket az ábrán látható módon. SS 1, NEÉs SE páronként merőlegesek, így a koordinátatengelyeket ezek mentén irányíthatja. Megkapjuk a koordinátákat:

C1 (0; 0; 1), E (; 0; 0), B 1 (0; 1; 1).

2) Keresse meg az egyenesek irányvektorainak koordinátáit! 1-től 1-igÉs C 1 E:

(0;1;0), (;0;-1).

3) Keresse meg a közötti szög koszinuszát! 1-től 1-igÉs C 1 E segítségével skaláris szorzat vektorok és:

cos β = = 0 => β = 90° => C 1 E – a szükséges távolság.

4)C 1 E = = 2.

Következtetés: tudás különböző megközelítések a sztereometrikus problémák megoldásához lehetővé teszi, hogy bármely tanuló számára kiválaszthassa a kívánt módszert, pl. amelyet a hallgató magabiztosan elsajátít, segít elkerülni a hibákat, a probléma sikeres megoldásához és megszerzéséhez vezet jó eredmény a vizsgán. A koordináta-módszer előnye a többi módszerrel szemben, hogy kevesebb sztereometrikus megfontolást és látásmódot igényel, és olyan képletek használatán alapul, amelyek számos, a hallgatók számára ismertebb planimetriai és algebrai analógiát tartalmaznak.

Az óra formája a tanári magyarázat és a tanulók frontális kollektív munkájának kombinációja.

A szóban forgó poliédereket egy videoprojektor segítségével jelenítik meg a képernyőn, ami lehetővé teszi az összehasonlítást különböző módokon megoldásokat.

Házi feladat: oldja meg a 3. feladatot más módon, például a három merőleges tétel segítségével .

Irodalom

1. Ershova A.P., Goloborodko V.V. Független és tesztpapírok geometriából 11. évfolyamra – M.: ILEKSA, – 2010. – 208 p.

2. Geometria, 10-11: tankönyv számára oktatási intézmények: alap- és profilszintek / L.S., V.F. Butuzov, S.B. Kadomtsev et al. - M.: Oktatás, 2007. - 256 p.

3. Egységes államvizsga-2012. Matematika: standard vizsgalehetőségek: 10 lehetőség / szerk. A. L. Semenova, I. V. Jascsenko. – M.: Nemzeti nevelés, 2011. – 112 p. – (USE-2012. FIPI - iskola).

A cikk a síkok közötti szög megállapításáról szól. A definíció megadása után grafikus illusztrációt adunk, és részletesen megvizsgáljuk a koordináták megtalálásának módszerét a módszerrel. A metsző síkok képletét kapjuk, amely tartalmazza a normálvektorok koordinátáit.

Yandex.RTB R-A-339285-1

Az anyag olyan adatokat és fogalmakat fog használni, amelyeket korábban a tér síkjáról és vonaláról szóló cikkekben tanulmányoztak. Először is át kell térnünk az érvelésre, amely lehetővé teszi számunkra, hogy bizonyos megközelítést alkalmazzunk a két egymást metsző sík közötti szög meghatározásához.

Két egymást metsző γ 1 és γ 2 sík adott. A kereszteződésük a c jelölést kapja. A χ sík felépítése e síkok metszéspontjához kapcsolódik. A χ sík c egyenesként halad át az M ponton. A γ 1 és γ 2 síkok metszéspontja a χ sík segítségével történik. A γ 1-et és χ-t metsző egyenest a egyenesnek, a γ 2-t és χ-t b egyenesnek vesszük. Azt találjuk, hogy az a és b egyenesek metszéspontja adja az M pontot.

Az M pont elhelyezkedése nem befolyásolja a metsző a és b egyenesek közötti szöget, az M pont pedig azon a c egyenesen található, amelyen a χ sík áthalad.

A c egyenesre merőleges és a χ síktól eltérő χ 1 síkot kell megszerkeszteni. A γ 1 és γ 2 síkok χ 1 segítségével történő metszéspontja az a 1 és b 1 egyenesek jelölését veszi fel.

Látható, hogy χ és χ 1 megszerkesztésénél az a és b egyenesek merőlegesek a c egyenesre, majd a 1, b 1 a c egyenesre merőlegesek. Ha a γ 1 síkban c egyenesre merőleges a és a 1 egyeneseket találunk, akkor párhuzamosnak tekinthetők. Ugyanígy b és b 1 helyzete a γ 2 síkban a c egyenesre merőlegesen jelzi párhuzamosságukat. Tehát meg kell tenni párhuzamos átvitelχ 1 sík χ-n, ahol két egybeeső egyenest kapunk a és a 1, b és b 1. Azt találjuk, hogy az a és b 1 metsző egyenesek közötti szög egyenlő az a és b metsző egyenesek szögével.

Nézzük az alábbi ábrát.

Ezt az állítást bizonyítja, hogy az a és b metsző egyenesek között olyan szög van, amely nem függ az M pont helyétől, vagyis a metszésponttól. Ezek a vonalak a γ 1 és γ 2 síkban helyezkednek el. Valójában a kapott szöget tekinthetjük két egymást metsző sík közötti szögnek.

Térjünk át a meglévő γ 1 és γ 2 metszősíkok közötti szög meghatározására.

1. definíció

Két egymást metsző γ 1 és γ 2 sík közötti szög az a és b egyenesek metszéspontja által alkotott szögnek nevezzük, ahol a γ 1 és γ 2 sík metszéspontja a c egyenesre merőleges χ síkkal.

Tekintsük az alábbi ábrát.

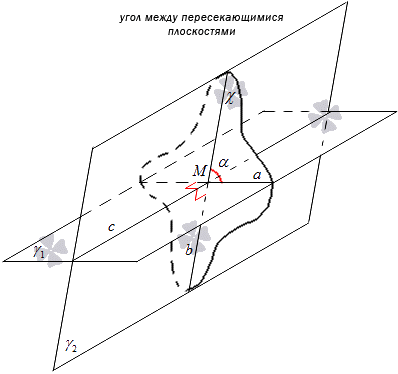
A határozat más formában is benyújtható. Amikor a γ 1 és γ 2 síkok metszik egymást, ahol c az az egyenes, amelyen metsződtek, jelöljünk ki egy M pontot, amelyen keresztül húzzuk a c egyenesre merőleges a és b egyeneseket, amelyek a γ 1 és γ 2 síkban helyezkednek el. az a és b egyenesek a síkok közötti szöget jelentik. A gyakorlatban ez a síkok közötti szög kialakítására alkalmazható.

Keresztezéskor 90 foknál kisebb szög alakul ki, azaz fokmérő szög érvényes egy ilyen típusú intervallumon (0, 90]. Ugyanakkor ezeket a síkokat merőlegesnek nevezzük, ha a metszéspontban derékszög alakul ki. párhuzamos síkok nullával egyenlőnek tekintendő.

A metsző síkok közötti szög megállapításának szokásos módja további konstrukciók végrehajtása. Ez segít a pontos meghatározásában, és ez megtehető egy háromszög egyenlőségének vagy hasonlóságának jeleivel, egy szög szinuszával és koszinuszával.

Tekintsük a problémák megoldását egy példán keresztül Egységes államvizsga problémák C blokk 2.

1. példa

Készlet kocka alakú A B C D A 1 B 1 C 1 D 1, ahol A B oldal = 2, A D = 3, A A 1 = 7, az E pont 4:3 arányban osztja az A A 1 oldalt. Határozzuk meg az A B C és B E D 1 síkok közötti szöget!

Megoldás

Az érthetőség kedvéért rajzot kell készíteni. Ezt értjük

Vizuális ábrázolásra van szükség, hogy kényelmesebb legyen a síkok közötti szöggel dolgozni.

Meghatározzuk azt az egyenest, amely mentén az A B C és B E D 1 síkok metszéspontja következik be. A B pont egy közös pont. Találni kéne másikat közös pont kereszteződések. Tekintsük a D A és D 1 E egyeneseket, amelyek ugyanabban az A D D 1 síkban helyezkednek el. Helyük nem párhuzamosságra utal, ez azt jelenti, hogy van közös metszéspontjuk.

A D A egyenes azonban az A B C síkban, a D 1 E pedig a B E D 1 síkban található. Ebből azt kapjuk, hogy az egyenesek D AÉs D 1 E közös metszéspontjuk van, ami közös az A B C és a B E D 1 síkra. A vonalak metszéspontját jelzi D Aés D 1 E F betű. Ebből azt kapjuk, hogy B F az az egyenes, amely mentén A B C és B E D 1 síkok metszik egymást.

Nézzük az alábbi ábrát.

A válasz megszerzéséhez az A B C és B E D 1 síkban elhelyezkedő, a B F egyenesen elhelyezkedő és arra merőleges ponton átmenő egyeneseket kell megszerkeszteni. Ekkor az ezen egyenesek közötti szöget az A B C és B E D 1 síkok közötti kívánt szögnek tekintjük.

Ebből láthatjuk, hogy az A pont az E pont vetülete az A B C síkra. Egy egyenest kell húzni, amely a B F egyenest derékszögben metszi az M pontban. Látható, hogy az A M egyenes a vetület az E M egyenesből az A B C síkra, azokra az A M ⊥ B F merőlegesekre vonatkozó tétel alapján. Vegye figyelembe az alábbi képet.

∠ A M E az A B C és B E D 1 síkok által alkotott kívánt szög. Az eredményül kapott A E M háromszögből csak akkor találhatjuk meg a szög szinuszát, koszinuszát vagy érintőjét, majd magát a szöget is, csak ha ismerjük a két oldalát. Feltétellel azt kapjuk, hogy az A E hosszt így találjuk meg: az A A 1 egyenest E ponttal osztjuk 4:3 arányban, ami azt jelenti, hogy az egyenes teljes hossza 7 rész, ekkor A E = 4 rész. Találunk egy M.

Meg kell fontolni derékszögű háromszög A B F . Van egy A derékszögünk, melynek magassága A M. Az A B = 2 feltételből akkor a D D 1 F és A E F háromszögek hasonlóságával megtalálhatjuk az A F hosszúságot. Azt kapjuk, hogy A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Meg kell találni az A B F háromszög B F oldalának hosszát a Pitagorasz-tétel segítségével. Azt kapjuk, hogy B F  = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Az A M oldal hossza az A B F háromszög területén keresztül található. Megvan, hogy a terület egyenlő lehet S A B C = 1 2 · A B · A F és S A B C = 1 2 · B F · A M értékkel.

Azt kapjuk, hogy A M = A B A F B F = 2 4 2 5 = 4 5 5

Ekkor megtaláljuk az A E M háromszög szögének érintőjének értékét.

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Az A B C és B E D 1 síkok metszéspontjával kapott kívánt szög egyenlő a r c t g 5 -tel, majd egyszerűsítéssel a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 értéket kapjuk.

Válasz: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

A metsző vonalak közötti szög megállapításának néhány esetét a segítségével határozzuk meg Koordináta sík O x y z és a koordináta módszer. Nézzük meg közelebbről.

Ha olyan feladatot kapunk, ahol meg kell találni a γ 1 és γ 2 metszősíkok közötti szöget, akkor a kívánt szöget α-val jelöljük.

Akkor adott rendszer A koordináták azt mutatják, hogy megvannak a γ 1 és γ 2 metszősíkok normálvektorainak koordinátái. Ekkor jelöljük, hogy n 1 → = n 1 x, n 1 y, n 1 z a γ 1 sík normálvektora, és n 2 → = (n 2 x, n 2 y, n 2 z) - a γ 2 sík. Tekintsük ezen síkok közötti szög részletes meghatározását a vektorok koordinátái alapján.

Ki kell jelölni azt az egyenest, amely mentén a γ 1 és γ 2 síkok metszik a c betűt. A c egyenesen van egy M pont, amelyen keresztül egy c-re merőleges χ síkot rajzolunk. A χ sík az a és b egyenesek mentén az M pontban metszi a γ 1 és γ 2 síkot. a definícióból az következik, hogy a metsző γ 1 és γ 2 síkok közötti szög egyenlő az ezekhez a síkokhoz tartozó a és b metsző egyenesek szögével.

A χ síkban ábrázolunk normálvektorokat az M pontból, és jelöljük őket n 1 → és n 2 → . Az n 1 → vektor az a egyenesre merőleges egyenesen, az n 2 → vektor pedig a b egyenesre merőlegesen helyezkedik el. Innentől azt kapjuk adott repülőgépχ az a egyenes normálvektora n 1 →, a b egyenesé pedig n 2 →. Tekintsük az alábbi ábrát.

Innen kapunk egy képletet, amellyel a metsző egyenesek szögének szinuszát a vektorok koordinátái segítségével számíthatjuk ki. Megállapítottuk, hogy az a és b egyenesek közötti szög koszinusza megegyezik a γ 1 és γ 2 metszősíkok közötti koszinuszával, amely a cos képletekα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, ahol azt kapjuk, hogy n 1 → = (n 1 x, n 1 y, n 1 z) és n 2 → = (n 2 x, n 2 y, n 2 z) a koordinátái az ábrázolt síkok vektorai.

A metsző vonalak közötti szöget a képlet segítségével számítjuk ki

α = a rc cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

2. példa

A feltétel szerint a paralelepipedon A B C D A 1 B 1 C 1 D 1 adott , ahol A B = 2, A D = 3, A A 1 = 7, és az E pont osztja az A A 1 4:3 oldalt. Határozzuk meg az A B C és B E D 1 síkok közötti szöget!

Megoldás

A feltételből jól látható, hogy oldalai páronként merőlegesek. Ez azt jelenti, hogy be kell vezetni egy O x y z koordinátarendszert a C pont csúcsával és az O x, O y, O z koordinátatengelyekkel. Be kell állítani az irányt a megfelelő oldalakra. Tekintsük az alábbi ábrát.

Metsző síkok A B CÉs B E D 1 olyan szöget alkotunk, amely az α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n képlettel kereshető 2 y 2 + n 2 z 2, amelyben n 1 → = (n 1 x, n 1 y, n 1 z) és n 2 → = (n 2 x, n 2 y, n 2 z ) normálvektorai ezeket a repülőket. Meg kell határozni a koordinátákat. Az ábrából azt látjuk koordináta tengely O x y egybeesik az A B C síkkal, ami azt jelenti, hogy a koordináták normál vektor k → egyenlő az n 1 → = k → = (0, 0, 1) értékkel.

Felvesszük a B E D 1 sík normálvektorát vektor termék B E → és B D 1 → , ahol koordinátáikat koordinátákkal találjuk meg szélsőséges pontok B, E, D 1, amelyeket a feladat feltételei alapján határozunk meg.

Azt kapjuk, hogy B (0, 3, 0), D 1 (2, 0, 7). Mivel A E E A 1 = 4 3, az A 2, 3, 0, A 1 2, 3, 7 pontok koordinátáiból E 2, 3, 4-et találunk. Azt találjuk, hogy B E → = (2, 0, 4), B D 1 → = 2, - 3, 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · i → - 6 j → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

A talált koordinátákat be kell cserélni az ív koszinuszon keresztüli szög kiszámításához szükséges képletbe. Kapunk

α = a rc cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

A koordináta módszer hasonló eredményt ad.

Válasz: a r c cos 6 6 .

A végső probléma a metsző síkok közötti szög meghatározása a síkok ismert egyenletei alapján történik.

3. példa

Számítsa ki a szög szinuszát, koszinuszát és a két egymást metsző egyenes által alkotott szög értékét, amelyeket az O x y z koordinátarendszerben definiálunk, és a 2 x - 4 y + z + 1 = 0 és 3 y - z egyenletekkel adjuk meg. - 1 = 0.

Megoldás

Egy téma tanulmányozásakor általános egyenlet Az A x + B y + C z + D = 0 alakú egyenesből kiderült, hogy A, B, C együtthatók a normálvektor koordinátáival. Ez azt jelenti, hogy n 1 → = 2, - 4, 1 és n 2 → = 0, 3, - 1 az adott egyenesek normálvektorai.

A metsző síkok kívánt szögének kiszámításához szükséges képletbe be kell cserélni a síkok normálvektorainak koordinátáit. Akkor azt kapjuk

α = a rc cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Innen azt kapjuk, hogy a szög koszinusza cos α = 13 210 alakot ölt. Ekkor a metsző egyenesek szöge nem tompa. Behelyettesítés trigonometrikus azonosság, azt találjuk, hogy a szög szinuszának értéke egyenlő a kifejezéssel. Számoljuk ki és találjuk meg

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Válasz: sin α = 41 210, cos α = 13 210, α = a r c cos 13 210 = a r c sin 41 210.

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt

Feladat 1. Egy egyenes alapja négyszögű prizma ABCDA 1 B 1 C 1 D 1 – ABCD téglalap, amelyben AB = 5, AD = 11. Határozza meg a prizma alapjának síkja és az AD él közepén átmenő szög érintőjét merőlegesen a BD 1 egyenes, ha az AC és B 1 D 1 egyenesek távolsága 12. Megoldás. Vezessünk be egy koordináta-rendszert. B(0;0;0), A(5;0;0), C(0;11;0), D 1 (5;11;12) A normál koordinátái a metszetsíkhoz: A normál koordinátái az alapsík: - éles sarok, akkor D A B C D1D1 A1A1 B1B1 C1C1 x y z N Síkok közötti szög Válasz: 0,5. Nenasheva N.G. matematika tanár GBOU középiskola 985

2. feladat A SABC háromszög alakú piramis alján egy téglalap található ABC háromszög. Az A szög egyenes. AC = 8, BC = 219. Az SA gúla magassága 6. Az M pontot az AC élre vesszük úgy, hogy AM = 2. Az M ponton, a B csúcson és az N ponton át - a közepén - egy α síkot húzunk. él SC. megtalálja diéderes szög, sík alkotjaα és a gúla alapjának síkja. A S x B C M N y z Megoldás. Vezessünk be egy koordinátarendszert. Ekkor A (0;0;0), C (0;8;0), M (0;2;0), N (0;4;3), S (0;0;6), Normál a síkra ( ABC) vektor Sík normál (PMN) Síkok közötti szög Válasz: 60°. Síkegyenlet (ВМN): Nenasheva N.G. matematika tanár GBOU középiskola 985

3. feladat A PABCD négyszöggúla alapja egy négyzet, amelynek oldala 6, a PD oldaléle merőleges az alap síkjára és egyenlő 6-tal. Határozzuk meg a (BDP) és (BCP) síkok közötti szöget! Megoldás. 1. Vegyük a DF mediánját egyenlő szárú háromszög CDP (BC = PD = 6) DF PC-t jelent. Abból pedig, hogy BC (CDP), az következik, hogy DF BC, ami DF (PCB) A D C B P F 2. Mivel AC DB és AC DP, akkor AC (BDP) 3. Így a síkok közötti szög (BDP) ill. (BCP ) a következő feltételből található: Síkok közötti szög Nenasheva N.G. matematika tanár GBOU középiskola 985

3. feladat A PABCD négyszöggúla alapja egy négyzet, amelynek oldala 6, a PD oldaléle merőleges az alap síkjára és egyenlő 6-tal. Határozzuk meg a (BDP) és (BCP) síkok közötti szöget! Megoldás.4. Válasszunk egy koordináta-rendszert. A pontok koordinátái: 5. Ekkor a vektorok a következő koordinátákkal rendelkeznek: 6. Az értékeket kiszámolva azt találjuk:, majd A D C B P F z x y A síkok közötti szög Válasz: Nenasheva N.G. matematika tanár GBOU középiskola 985

4. feladat Az ABCDA 1 B 1 C 1 D 1 egységkockában keresse meg az (AD 1 E) és (D 1 FC) síkok közötti szöget, ahol az E és F pontok az A 1 B 1 és az élek felezőpontjai. B 1 C 1, ill. Megoldás: 1. Vezessünk be egy téglalap alakú koordinátarendszert és határozzuk meg a pontok koordinátáit: 2. Készítsük el a sík egyenletét (AD 1 E): 3. Készítsük el a sík egyenletét (D 1 FC): - normál a sík vektora (AD 1 E). - a sík normálvektora (D 1 FC). Síkok közötti szög x y z Nenasheva N.G. matematika tanár GBOU középiskola 985

4. feladat Az ABCDA 1 B 1 C 1 D 1 egységkockában keresse meg az (AD 1 E) és (D 1 FC) síkok közötti szöget, ahol az E és F pontok az A 1 B 1 és az élek felezőpontjai. B 1 C 1, ill. Megoldás: 4. Keresse meg a síkok közötti szög koszinuszát a képlet segítségével. Válasz: A síkok közötti szög x y z Nenasheva N.G. matematika tanár GBOU középiskola 985

5. feladat Egy szabályos háromszög alakú gúla alapjának középpontját a közepével összekötő szakasz oldalsó borda, oldallal egyenlő okokból. Határozza meg a gúla szomszédos oldallapjai közötti szöget! Megoldás: x y z 1. Vezessünk be egy derékszögű koordináta-rendszert, és határozzuk meg az A, B, C pontok koordinátáit: K Legyen az alap oldala egyenlő 1-gyel. A határozottság érdekében tekintsük az SAC és SBC 2 lapokat. Keressük meg a koordinátákat. S pont: E Síkok közötti szög Nenasheva N.G. matematika tanár GBOU középiskola 985

5. feladat. Egy szabályos háromszög alakú gúla alapjának középpontját az oldalél közepével összekötő szakasz egyenlő az alap oldalával. Határozza meg a gúla szomszédos oldallapjai közötti szöget! Megoldás: x y z K E SO OSB-ről találjuk: Síkok közötti szög Nenasheva N.G. matematika tanár GBOU középiskola 985

5. feladat. Egy szabályos háromszög alakú gúla alapjának középpontját az oldalél közepével összekötő szakasz egyenlő az alap oldalával. Határozza meg a gúla szomszédos oldallapjai közötti szöget! Megoldás: x y z K E 3. Síkegyenlet (SAC): - sík normálvektor (SAC). 4. Síkegyenlet (SBC): - sík normálvektor (SBC). Síkok közötti szög Nenasheva N.G. matematika tanár GBOU középiskola 985

5. feladat. Egy szabályos háromszög alakú gúla alapjának középpontját az oldalél közepével összekötő szakasz egyenlő az alap oldalával. Határozza meg a gúla szomszédos oldallapjai közötti szöget! Megoldás: x y z K E 5. Keresse meg a síkok közötti szög koszinuszát a képlet segítségével Válasz: Síkok közötti szög Nenasheva N.G. matematika tanár GBOU középiskola 985

A koordináta-módszer használata szög kiszámításához

repülők között

A legtöbb általános módszer a szög megtalálásasíkok között - a koordináta módszer (néha vektorok segítségével). Akkor használható, ha az összes többit kipróbálták. De vannak olyan helyzetek, amikor a koordináta-módszert azonnal érdemes alkalmazni, mégpedig akkor, ha a koordináta-rendszer természetes kapcsolatban áll a problémafelvetésben megadott poliéderrel, pl. Jól látható három páronkénti merőleges vonal, amelyeken koordinátatengelyek adhatók meg. Az ilyen poliéderek egy téglalap alakú paralelepipedon és egy szabályos négyszög alakú piramis. Az első esetben a koordinátarendszer az egyik csúcsból kinyúló élekkel (1. ábra), a másodikban az alap magasságával és átlóival határozható meg (2. ábra).

A koordináta módszer alkalmazása a következő.

Bemutatott téglalap alakú rendszer koordináták a térben. Célszerű „természetes” módon bevezetni - „kapcsolni” páronkénti merőleges vonalak hármasához, amelyeknek közös pontja van.

Minden olyan síkra, amelyek között meg kell keresni a szöget, egy egyenletet készítünk. Egy ilyen egyenlet létrehozásának legegyszerűbb módja, ha ismerjük a sík három olyan pontjának koordinátáit, amelyek nem ugyanazon az egyenesen helyezkednek el.

A sík egyenlete in Általános nézetúgy néz ki, mint a Ax + By + Cz + D = 0.

A, B együtthatók, C ebben az egyenletben a sík normálvektorának koordinátái (vektor, merőleges a síkra). Ezután meghatározzuk a normálvektorok hosszát és skaláris szorzatát azokhoz a síkokhoz, amelyek között a szöget meg kell keresni. Ha ezeknek a vektoroknak a koordinátái(A 1, B 1; C 1) és (A 2; B 2; C 2 ), majd a kívánt szögetképlettel számítjuk ki

Megjegyzés. Emlékeztetni kell arra, hogy a vektorok közötti szög (szemben a síkok közötti szöggel) lehet tompa, és az esetleges bizonytalanság elkerülése érdekében a képlet jobb oldalán lévő számláló modult tartalmaz.

Oldja meg ezt a feladatot a koordináta módszerrel.

1. feladat Adott egy ABCDA 1 B 1 C 1 D 1 kocka. A K pont az AD él közepe, az L pont a CD él közepe. Miért egyenlő a szöggel A síkok között 1 KL és A 1 AD?

Megoldás . Legyen a koordinátarendszer origója a pontban A, a koordinátatengelyek pedig a sugarak mentén mennek AD, AB, AA 1 (3. ábra). Vegyük a kocka szélét 2-nek (kényelmes kettéosztani). Ezután a pontok koordinátái A1, K, L jelentése a következő: A1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).

Rizs. 3

Írjuk fel a sík egyenletét A 1 K L általában. Ezután behelyettesítjük a sík kiválasztott pontjainak koordinátáit. Kapunk egy három egyenletrendszert négy ismeretlennel:

Fejezzük ki az együtthatókat A, B, C-től D-ig és eljutunk az egyenlethez

Mindkét részt felosztva D (miért D = 0?), majd -2-vel megszorozva megkapjuk a sík egyenletét A 1 KL: 2x - 2 y + z - 2 = 0. Ekkor ennek a síknak a normálvektorának koordinátái vannak (2: -2; 1). Sík egyenlet Az 1 AD értéke: y=0, és a hozzá tartozó normálvektor koordinátái például (0; 2: 0). A síkok közötti szög koszinuszának fenti képlete szerint a következőket kapjuk: