1. és 2. típusú nem megfelelő integrálok. Nem megfelelő integrálok

Nem megfelelő integrál végtelen integrációs korláttal

Néha az ilyen nem megfelelő integrált az első típusú nem megfelelő integrálnak is nevezik..gif" width="49" height="19 src=">.

Kevésbé gyakoriak azok az integrálok, amelyeknek egy-két végtelen alsó határa van végtelen határok: .

A legnépszerűbb esetet vesszük figyelembe: https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Nem, nem mindig. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Ábrázoljuk a rajzon az integrandusfüggvény grafikonját. Ebben az esetben egy tipikus grafikon és görbe trapéz így néz ki:

Nem megfelelő integrálhttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", vagyis a terület is végtelen. Lehet, hogy így van. Ebben az esetben azt mondják, hogy a nem megfelelő integrál eltér.

2) De. Bármilyen paradoxon is hangzik, egy végtelen alak területe egyenlő lehet... egy véges számmal! Például: .. A második esetben a nem megfelelő integrál konvergál.

Mi történik, ha egy végtelen görbe trapéz a tengely alatt helyezkedik el?.gif" width="217" height="51 src=">.

: .

1. példa

Az integráns függvény https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, ami azt jelenti, hogy minden rendben van, és a nem megfelelő integrál kiszámítható a " standard” módszerrel.

Képletünk alkalmazása https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

Vagyis a nem megfelelő integrál eltér, és az árnyékolt terület ívelt trapéz egyenlő a végtelennel.

A nem megfelelő integrálok megoldásánál nagyon fontos tudni, hogyan néznek ki az alapvető elemi függvények grafikonjai!

2. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Készítsük el a rajzot:

Először a következőket jegyezzük meg: az integrandus a félintervallumon folytonos. Jó..gif" width="327" height="53">

(1) Vegyük a legegyszerűbb integrálját teljesítmény funkció(ez speciális eset sok táblázatban megjelenik). Jobb, ha a mínusz jelet azonnal a határjelen túlra mozgatja, hogy ne akadályozza a további számításokat.

(2) A felső és alsó határt a Newton-Leibniz képlet segítségével helyettesítjük.

(3) Hangsúlyozzuk, hogy https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Uraim, ezt sokáig meg kell érteni régen), és egyszerűsítse a választ.

Itt egy végtelen görbe trapéz területe véges szám! Hihetetlen, de igaz.

3. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Az integrandus folyamatos a .

Először próbáljuk meg megtalálni az antiderivatív függvényt ( határozatlan integrál).

Melyik táblázatintegrálhoz hasonlít az integrandus? Arktangensre emlékeztet: . Ezek a megfontolások azt sugallják, hogy jó lenne egy négyzet a nevezőben. Ez cserével történik.

Cseréljük:

Mindig hasznos ellenőrzést végezni, azaz megkülönböztetni a kapott eredményt:

Most megtaláljuk a nem megfelelő integrált:

(1) A megoldást a képlet szerint írjuk fel . Jobb, ha az állandót azonnal a határjelen túlra mozgatjuk, hogy ne zavarja a további számításokat.

(2) A felső és alsó határértéket a Newton-Leibniz képlet szerint helyettesítjük..gif" width="56" height="19 src=">? Lásd az arctangens grafikonját a már többször ajánlott cikkben.

(3) Megkapjuk a végső választ. Egy tény, amit hasznos fejből tudni.

Előfordulhat, hogy a haladók nem találják meg külön a határozatlan integrált, és nem alkalmazzák a helyettesítési módszert, hanem inkább azt a módszert használják, hogy a differenciáljel alatti függvényt behelyettesítik, és a nem megfelelő integrált „azonnal” megoldják. Ebben az esetben a megoldásnak valahogy így kell kinéznie:

“

Az integrand függvény folyamatos a https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104"> oldalon
“

4. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

! Ez tipikus példa, és nagyon gyakran előfordulnak hasonló integrálok. Dolgozd ki jól! Antiderivatív funkció itt található egy teljes négyzet elkülönítésének módszerével.

5. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Ez az integrál részletesen megoldható, azaz először változó változtatással keressük meg a határozatlan integrált. Vagy "azonnal" megoldhatja - a függvényt a differenciáljel alá foglalva.

Korlátlan függvények nem megfelelő integráljai

Néha az ilyen nem megfelelő integrálokat a második típusú nem megfelelő integráloknak nevezik. Nem megfelelő integrálok A második típus alattomosan „titkosított” a szokásos határozott integrál alá, és pontosan ugyanúgy néz ki: ..gif" width="39" height="15 src=">, 2) vagy pontban, 3) vagy mindkét pontot egyszerre, 4) vagy akár az integrációs szegmenst is figyelembe vesszük, a 3-4 esethez a cikk végén található egy hivatkozás.

Csak egy példa, hogy egyértelmű legyen: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, akkor a nevezőnk nullára megy, vagyis az integrandus egyszerűen nem létezik ezen a ponton!

Általában egy nem megfelelő integrál elemzésekor mindig mindkét integrációs korlátot be kell cserélnie az integrandusba..jpg" alt="Nem megfelelő integrál, szakadási pont az integráció alsó határán" width="323" height="380">!}

Itt minden majdnem ugyanaz, mint az első típusú integrálban.
Integrálunk numerikus területtel egyenlőárnyékolt íves trapéz, amely felül nincs korlátozva. Ebben az esetben két lehetőség lehet: a nem megfelelő integrál divergál (a terület végtelen), vagy a nem megfelelő integrál egy véges számmal (vagyis egy végtelen alak területe véges!).

Már csak a Newton-Leibniz képlet módosítása van hátra. Határ segítségével is módosul, de a határ már nem a végtelen felé hajlik, hanem értékelnihttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> jobbra.

6. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Az integrandus egy ponton végtelen folytonossági hiányossággal rendelkezik (ne felejtse el szóban vagy piszkozaton ellenőrizni, hogy minden rendben van-e a felső határértékkel!)

Először is számítsuk ki a határozatlan integrált:

Csere:

Számítsuk ki a nem megfelelő integrált:

(1) Mi újság itt? Megoldástechnika terén gyakorlatilag semmi. Csak a limit ikon alatti bejegyzés változott: . Az összeadás azt jelenti, hogy a jobb oldali értékre törekszünk (ami logikus – lásd a grafikont). Az ilyen határértéket a határelméletben egyoldalú határértéknek nevezzük. IN ebben az esetben Van egy jobbkezes korlátunk.

(2) A felső és alsó határt a Newton-Leibniz képlet segítségével helyettesítjük.

(3) Nézzük meg a következőt: https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Hogyan határozható meg, hová kerüljön a kifejezés? Durván szólva , csak be kell cserélnie az értéket, be kell cserélnie háromnegyedet, és jeleznie kell, hogy fésülje a választ.

Ebben az esetben a nem megfelelő integrál egyenlő egy negatív számmal.

7. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

8. példa

Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját.

Ha az integrandus nem létezik a ponton

Egy ilyen helytelen integrálhoz tartozó végtelen görbe trapéz alapvetően így néz ki:

Itt minden teljesen ugyanaz, kivéve, hogy a mi határunk hajlamos értékelnihttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> végtelenül közel kell közelednünk a törésponthoz balra.

Határozott integrál, mint az integrálösszeg határa

csak a feltételek teljesülése esetén létezhet (vagyis van egy bizonyos végső értéke).

Ha e feltételek közül legalább egy megsérül, a meghatározás értelmét veszti. Valóban, egy végtelen szakasz esetén például [ a; ) nem osztható fel n véges hosszúságú részek
, ami ráadásul a szegmensek számának növekedésével nullára dőlne. A korlátlan esetében valamikor Vel[a; b] sérül az önkényes pontkiválasztás követelménye részszakaszokon – nem választható ki =Vel, mivel a függvény értéke ezen a ponton definiálatlan. Azonban még ezekre az esetekre is lehetőség van a határozott integrál fogalmának általánosítására, ha egy másik szakaszt bevezetünk a határvonalba. A végtelen intervallumok feletti integrálokat és a nem folytonos (korlátlan) függvényeket hívjuk nem a sajátod.

Meghatározás.

Legyen a függvény
a [ a; ) és bármely véges intervallumra integrálható [ a; b], azaz létezik
bárkinek b > a. Típuskorlát
hívott helytelen integrál első fajta (vagy nem megfelelő integrált egy végtelen intervallumon) és jelölje
.

Tehát definíció szerint
=
.

Ha a jobb oldali határ létezik és véges, akkor a nem megfelelő integrál
hívott konvergens . Ha ez a határ végtelen, vagy egyáltalán nem létezik, akkor azt mondják, hogy a nem megfelelő integrál eltér .

Hasonlóképpen bevezethetjük a függvény nem megfelelő integráljának fogalmát
intervallum mentén (–; b]:

=
.

És a függvény nem megfelelő integrálja
az intervallum felett (–; +) a fent bevezetett integrálok összegeként van definiálva:

=
+
,

Ahol A– tetszőleges pont. Ez az integrál konvergál, ha mindkét tag konvergál, és divergál, ha legalább az egyik tag eltér.

Geometriai szempontból az integrál
,
, meghatározza számérték egy végtelen görbe trapéz területe, amelyet felette a függvény grafikonja határol
, balra – egyenes
, alulról – az OX tengelyével. Az integrál konvergenciája azt jelenti, hogy létezik egy ilyen trapéz véges területe és egyenlősége egy mozgatható jobb falú görbe vonalú trapéz területének határával.
.

Egy végtelen határú integrál esetén általánosíthatunk Newton-Leibniz képlet:

=
=F( + ) – F( a),

ahol F( + ) =
. Ha ez a határ létezik, akkor az integrál konvergál, in egyébként– eltér.

Megfontoltuk a határozott integrál fogalmának a végtelen intervallum esetére történő általánosítását.

Tekintsünk most egy általánosítást egy korlátlan függvény esetére.

Meghatározás

Legyen a függvény
a [ a; b), korlátlan a pont bizonyos környezetében b, és bármely intervallumon folyamatos
, ahol>0 (és ezért integrálható ezen az intervallumon, pl.
létezik). Típuskorlát
hívott a második típusú helytelen integrál (vagy egy korlátlan függvény nem megfelelő integrálja), és jelöljük
.

Így a korlátlan helytelen integrálja a pontban b függvények definíció szerint léteznek

=
.

Ha a jobb oldali határérték létezik és véges, akkor az integrált hívjuk konvergens. Ha nincs véges határ, akkor a nem megfelelő integrált hívjuk meg divergens.

Hasonlóképpen definiálhatjuk a függvény nem megfelelő integrálját
amelynek a pontban végtelen folytonossági hiánya van A:

=
.

Ha a funkció
végtelen folytonossági hiánya van a belső pontban Vel
, akkor a nem megfelelő integrált a következőképpen definiáljuk

=
+
=
+
.

Ez az integrál konvergál, ha mindkét tag konvergál, és divergál, ha legalább egy tag eltér.

Geometriai szempontból a korlátlan függvény nem megfelelő integrálja a korlátlan görbe trapéz területét is jellemzi:

Mivel a nem megfelelő integrált egy határozott integrálból a határértékre való átadással vezetjük le, a határozott integrál összes tulajdonsága átvihető (megfelelő finomításokkal) az első és a második típusú nem megfelelő integrálokra.

Sok olyan problémában, amely nem megfelelő integrálokhoz vezet, nem szükséges tudni, hogy ez az integrál mivel egyenlő, elég csak ellenőrizni a konvergenciáját vagy divergenciáját. Erre használnak a konvergencia jelei. A nem megfelelő integrálok konvergenciájának jelei:

1) Összehasonlító jel.

Legyen mindenkié X

. Aztán ha
konvergál, majd konvergál
, és

. Ha
eltér, majd eltér és
.

2) Ha konvergál
, majd konvergál és
(az utolsó integrált ebben az esetben nevezzük abszolút konvergens).

A korlátlan függvények nem megfelelő integráljainak konvergenciájának és divergenciájának kritériumai hasonlóak a fentebb megfogalmazottakhoz.

Példák problémamegoldásra.

1. példa

A)
; b)
; V)

G)
; d)
.

Megoldás.

a) Értelemszerűen a következőkkel rendelkezünk:

.

b) Hasonlóképpen

Ezért ez az integrál konvergál és egyenlő .

c) Definíció szerint
=
+
, és A – tetszőleges szám. Tegyük a mi esetünkbe
, akkor kapjuk:

Ez az integrál konvergál.

Ez azt jelenti, hogy ez az integrál eltér.

e) Gondoljuk át
.

Az integrandus antideriváltjának megtalálásához a részenkénti integráció módszerét kell alkalmazni. Akkor kapjuk:
Mivel egyik sem
, sem

nem létezik, akkor nem létezik és

Ezért ez az integrál divergál.

2. példa Vizsgáljuk meg az integrál konvergenciáját! n.

Megoldás.

attól függően
at

nálunk van:
Ha
, Azt

nálunk van:
Ha
És. Ezért az integrál eltér.
, A

=,

, Akkor

nálunk van:
Ha

Ezért az integrál konvergál.

ezért az integrál eltér.

Így,

3. példa

A)
Számítsa ki a nem megfelelő integrált, vagy állapítsa meg divergenciáját:
;
.

Megoldás.

b)
;
V)

a) Integrál

.

a második típusú nem megfelelő integrál, mivel az integrandus .

nem korlátozott egy ponton
. Akkor definíció szerint
. Ezért ez az integrál nem megfelelő a második fajtához, és definíció szerint

Ezért az integrál eltér.

c) Fontolja meg
. Integrand
két ponton végtelen hézagot szenved:
És
, amelyek közül az első az integrációs intervallumhoz tartozik
. Ezért ez az integrál a második típusú nem megfelelő integrál. Akkor definíció szerint

=

=

.

Ezért az integrál konvergál és egyenlő
.

Határozott integrálok online az oldalon a diákok és az iskolások számára, hogy megszilárdítsák az általuk feldolgozott anyagot. És gyakorolja gyakorlati készségeit. A határozott integrálok pillanatok alatti teljes online megoldása segít meghatározni a folyamat minden szakaszát – a határozott online integrált. Bizonyos integrálok az oldalon a diákok és iskolások számára, hogy teljes mértékben megszilárdítsák az általuk feldolgozott anyagot, és gyakorolják gyakorlati készségeiket. A határozott integrálok pillanatok alatti teljes online megoldása segít meghatározni a folyamat minden szakaszát – a határozott online integrált. Számunkra egy határozott integrál online felvétele nem tűnik túl természetesnek, miután tanulmányoztuk ezt a témát kiemelkedő szerzők könyve alapján. Nagyon köszönjük nekik, és kifejezzük tiszteletünket ezeknek a személyeknek. Segít meghatározni a határozott integrált online szolgáltatás gyorsan kiszámítani az ilyen problémákat. Csak adja meg a helyes információkat, és minden rendben lesz! Bármilyen határozott integrál egy probléma megoldásaként javítja a tanulók írástudását. Minden lusta ember erről álmodik, és mi sem vagyunk kivételek, valljuk be őszintén. Ha mégis sikerül ingyenes megoldással online számolni egy határozott integrált, akkor kérjük, írja meg mindenkinek a weboldal címét, aki használni szeretné. Ahogy mondják, oszd meg hasznos link- és meg fogják köszönni jó emberek ingyen. Nagyon érdekes lesz egy olyan probléma elemzésének kérdése, amelyben egy bizonyos integrált a számológép önmagában old meg, nem pedig az értékes idő elpazarlásával. Ezért gépek, hogy az emberekért dolgozzanak. Bizonyos integrálok online megoldását azonban nem minden webhely képes kezelni, és ezt könnyű ellenőrizni, nevezetesen, hogy összetett példaés próbálja meg megoldani az egyes ilyen szolgáltatások segítségével. Érezni fogod a különbséget saját bőre. Gyakran nehéz erőfeszítés nélkül megtalálni egy határozott integrált online, és a válasz nevetségesnek tűnik az eredmény általános képének hátterében. Jobb lenne először egy fiatal harcos tanfolyamot végezni. A helytelen integrálok online megoldása először a határozatlan kiszámítására redukálódik, majd a határok elméletével az eredményül kapott kifejezésekből az A és B helyettesített határokkal általában egyoldalú határértékeket számítunk ki. Az Ön által megadott határozott integrált figyelembe véve online -val részletes megoldás, arra a következtetésre jutottunk, hogy az ötödik lépésben hibázott, mégpedig a Csebisev-változóhelyettesítő képlet használatakor. Legyen nagyon óvatos a további döntésében. Ha a határozott integrál online számológép Ha első alkalommal nem tudta elfogadni, akkor mindenekelőtt ellenőrizze az írott adatokat a megfelelő űrlapokon a weboldalon. Győződjön meg róla, hogy minden rendben van, és hajrá, Go-Go! Minden diák számára az akadály a nem megfelelő integrálok online kiszámítása magával a tanárral, mivel ez vagy vizsga, vagy kollokvium, vagy csak teszt egy páron.. Amint az adott nem megfelelő integrál online számológép a rendelkezésére áll, azonnal írja be adott funkciót, helyettesítse be a megadott integrációs korlátokat, és kattintson a Megoldás gombra, amely után teljes, részletes választ kaphat. Mégis jó, ha van egy ilyen csodálatos oldal, mint oldal, mert ingyenes, könnyen használható, és sok szekciót is tartalmaz. amelyet a tanulók mindennap használnak, ezek egyike egy határozott integrál online megoldással teljes formában. Ugyanebben a részben online kiszámíthatja a nem megfelelő integrált részletes megoldással a válasz további alkalmazásaihoz mind az intézetben, mind a mérnöki munkában. Úgy tűnik, hogy egy határozott integrál online meghatározása egyszerű dolga mindenkinek, ha előre megold egy ilyen példát a felső és a alsó határ, vagyis nem a Leibniz integrál, hanem a határozatlan integrál. De itt te és én kategorikusan nem értünk egyet, hiszen első pillantásra ez pont így tűnhet, de van egy lényeges különbség, szedjünk szét mindent. A megoldás nem kifejezetten ad ilyen határozott integrált, hanem a kifejezés határértékké való átalakításának következményeként. Más szóval, először meg kell oldania az integrált a határok szimbolikus értékeinek helyettesítésével, majd a határértéket a végtelenben vagy egy adott pontban kell kiszámítani. Ezért egy határozott integrál online kiszámítása egy megoldással nem jelent mást, mint a pontos megoldás bemutatását a Newton-Leibniz képlet segítségével. Ha figyelembe vesszük a határozott integrálszámítógépünket, akkor néhány másodperc alatt a szeme láttára segít kiszámolni. Ez a rohanás mindenkinek szükséges, aki a lehető leggyorsabban szeretné elvégezni a feladatot, és fel kell szabadulnia személyes ügyeire. Nem szabad olyan oldalakat keresni az interneten, amelyek regisztrációt kérnek, majd pénzt adnak az egyenlegéhez, mindezt annak érdekében, hogy néhány okos fickó készítsen megoldásokat bizonyos integrálokra állítólag online. Ne feledje, hogy a Math24 egy ingyenes szolgáltatás a megoldáshoz matematikai problémák, online is segítünk megtalálni a határozott integrált konkrét példák. Írja be az integrandust a megfelelő mezőbe, majd adjon meg vagy végtelen határértékeket (ebben az esetben a nem megfelelő integrálok megoldását a rendszer kiszámítja és online megkapja), vagy adja meg a számszerű vagy szimbolikus határértékeit és a határozott integrált online részletes megoldással A "Megoldás" gombra kattintás után megjelenik az oldalon. Ugye - nagyon egyszerű, nem igényel felesleges műveleteket, ingyenes, ami a legfontosabb, és ugyanakkor hatékony. A szolgáltatást saját maga is igénybe veheti, hogy egy bizonyos integrált online számológép maximális hasznot hozzon Önnek, és kényelmes állapotot kapjon anélkül, hogy a számítási folyamatok bonyolultságán túl stresszelne, hagyja, hogy mindent megteszünk Ön helyett, és megmutathassuk az erejét. számítástechnika modern világ. Ha belemerülsz a vadonba a legbonyolultabb képletekés önállóan tanulja meg a nem megfelelő integrálok számítását online, akkor ez dicséretes, és jogosult lehet a PhD-dolgozat megírására, de térjünk vissza a valóságba diákélet. Ki az a diák? Először is egy fiatal, energikus és jókedvű férfi, aki szeretne pihenni és házi feladatot csinálni! Ezért gondoskodtunk azokról a diákokról, akik nem megfelelő integrált online kalkulátort próbálnak találni a globális hálózat széles skáláján, és ez a figyelmed – az oldal a leghasznosabb online megoldó a fiatalok számára. Mellesleg, bár a mi szolgáltatásunkat asszisztensként mutatjuk be diákoknak, iskolásoknak, minden mérnök számára teljes mértékben megfelel, mert bármilyen típusú problémára képesek vagyunk, és azok megoldását professzionális formában mutatjuk be. Például egy határozott integrált online kínálunk teljes formában, szakaszosan, azaz mindegyikhez logikai blokk(részfeladatok) külön rekordot osztanak ki az összes számítással a folyamat során általános megoldás. Ez természetesen leegyszerűsíti a többlépcsős szekvenciális elrendezések érzékelését, és így az oldalprojekt előnye a hasonló szolgáltatásokkal szemben, hogy részletes megoldással találja meg a nem megfelelő integrálokat az interneten.

Határozott integrál

\[ I=\int_a^bf(x)dx \]

azzal a feltevéssel készült, hogy az $a,\,b$ számok végesek, az $f(x)$ pedig folytonos függvény. Ha ezen feltevések valamelyikét megsértjük, nem megfelelő integrálokról beszélünk.

10.1 1. típusú nem megfelelő integrálok

Az 1. típusú nem megfelelő integrál akkor fordul elő, ha az $a,\,b$ számok közül legalább az egyik végtelen.

10.1.1 Definíció és alapvető tulajdonságok

Nézzük először azt a helyzetet, amikor az integráció alsó határa véges, a felső határ pedig $+\infty$, a többi lehetőségről kicsit később fogunk beszélni. $f(x)$ esetén folytonos minden számunkra érdekes $x$ esetén, tekintsük az integrált

\begin(egyenlet) I=\int _a^(+\infty)f(x)dx. \quad(19) \label(inf1) \end(egyenlet)

Először is meg kell határoznunk ennek a kifejezésnek a jelentését. Ehhez bemutatjuk a függvényt

\[ I(N)=\int _a^(N)f(x)dx \]

és vegye figyelembe a viselkedését a $N\rightarrow +\infty$ esetén.

Meghatározás. Hadd létezzen végső határ

\[ A=\lim_(N \rightarrow +\infty)I(N)=\lim_(N \rightarrow +\infty)\int _a^(N)f(x)dx. \]

Ekkor azt mondjuk, hogy az 1. típusú (19) nem megfelelő integrál konvergens, és a $A$ értéket hozzárendeljük a függvénynek a $\left[ a, \, +\infty \right intervallumon; $. Ha a megadott határérték nem létezik, vagy egyenlő a $\pm \infty$ értékkel, akkor a (19) integrált divergálni kell.

Az 1. típusú konvergens nem megfelelő integrálok a közönséges határozott integrálok összes standard tulajdonságával rendelkeznek.

1. Ha $f(x)$, $g(x)$ integrálható a $\left[ a, \, +\infty \right)$ intervallumban, akkor ezek összege $f(x)+g(x) A $ is integrálható ebben az intervallumban, és \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx. \] 2. Ha a $f(x)$ integrálható a $\left[ a, \, +\infty \right)$ intervallumban, akkor bármely $C$ konstans esetén a $C\cdot f(x)$ függvény ezen az intervallumon is integrálható, és \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx. \] 3. Ha a $f(x)$ integrálható a $\left[ a, \, +\infty \right)$ intervallumban, és ezen az intervallumon a $f(x)>0$, akkor \[ \int _a^ (+\infty) f(x)dx\,>\,0. \] 4. Ha a $f(x)$ integrálható a $\left[ a, \, +\infty \right)$ intervallumban, akkor bármely $b>a$ esetén a \[ \int _b^(+ \infty) f(x)dx \] konvergál, és \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty ) f( x)dx \] (az integrál összeadódása az intervallumon belül).

Érvényesek a változó megváltoztatásának, részenkénti integrálásának stb. képletei is. (természetes rezervátumokkal).

Tekintsük most azt a lehetőséget, amikor az integráció alsó határa $-\infty$, a felső pedig véges, azaz. nézzük az integrálokat

\[ I=\int _(-\infty)^af(x)dx. \]

Ez a lehetőség azonban lecsökkenthető az előzőre, ha megváltoztatjuk a $x=-s$ változókat, majd helyenként módosítjuk az integráció határait, így

\[ I=\int _(-a)^(+\infty)g(s)ds, \]

$g(s)=f(-s)$. Tekintsük most azt az esetet, amikor két végtelen határ van, pl. integrál

\begin(egyenlet) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(egyenlet)

és $f(x)$ folyamatos minden $x \in \mathbb(R)$ esetén. Osszuk fel az intervallumot két részre: vegyük $c \in \mathbb(R)$-t, és vegyünk két integrált,

\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx. \]

Meghatározás. Ha mindkét $I_1$, $I_2$ integrál konvergál, akkor a (21) integrált konvergensnek nevezzük, és a $I=I_1+I_2$ értéket kapjuk (az intervallumon belüli additivitásnak megfelelően). Ha a $I_1$, $I_2$ integrálok közül legalább az egyik divergál, a (21) integrált divergensnek nevezzük.

Bizonyítható, hogy a (21) integrál konvergenciája nem függ a $c$ pont megválasztásától.

Az 1. típusú nem megfelelő integrálok $\left(-\infty, \, c \right]$ vagy $(-\infty, \, +\infty)$ integrációs intervallumokkal szintén rendelkeznek a határozott integrálok összes szabványos tulajdonságával (a megfelelő újrafogalmazás a választási integrációs intervallum figyelembevételével).

10.1.2. Vizsgálatok az 1. típusú nem megfelelő integrálok konvergenciájára

Tétel (az összehasonlítás első jele). Legyen $f(x)$, $g(x)$ folytonos $x>a$ és $0 a$ esetén. Majd

1. Ha a \[ \int _a^(+\infty)g(x)dx \] integrál konvergál, akkor a \[ \int _a^(+\infty)f(x)dx integrál konvergál. \] 2. Ha a \[ \int _a^(+\infty)f(x)dx \] integrál eltér, akkor a \[ \int _a^(+\infty)g(x)dx integrál divergál. \]

Tétel (második összehasonlítási kritérium). Legyen $f(x)$, $g(x)$ folytonos és pozitív $x>a$-ra, és legyen véges határ

\[ \theta = \lim_(x \rightarrow +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Aztán az integrálok

\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]

egyidejűleg konvergálnak vagy divergálnak.

Az első típusú nem megfelelő integrálok: a fogalom terjedése határozott integrál végtelen felső vagy alsó integrációs határú integrálok esetén, vagy mindkét integrálási határ végtelen.

A második típusú nem megfelelő integrálok: a határozott integrál fogalmának kiterjesztése a korlátlan függvények integráljaira, az integrandus nem létezik az integráció véges szegmensének véges számú pontjában, a végtelenbe fordulva.

Összehasonlításképpen. A határozott integrál fogalmának bevezetésekor azt feltételeztük, hogy a függvény f(x) folyamatos a [ a, b], és az integrációs szegmens véges, azaz számok korlátozzák, és nem a végtelen. Egyes feladatok e korlátozások feladásához vezetnek. Így jelennek meg a nem megfelelő integrálok.

A nem megfelelő integrál geometriai jelentése Egészen egyszerűen kiderül. Abban az esetben, ha egy függvény grafikonja y = f(x) a tengely felett van Ökör, a határozott integrál egy görbével határolt görbe vonalú trapéz területét fejezi ki y = f(x) , x tengely és ordináták x = a , x = b. A nem megfelelő integrál viszont egy korlátlan (végtelen) görbe vonalú trapéz területét fejezi ki, amely a vonalak közé van zárva y = f(x) (az alábbi képen - piros), x = aés az abszcissza tengely.

A helytelen integrálokat hasonlóképpen határozzuk meg más végtelen intervallumokhoz:

Egy végtelenül ívelt trapéz területe lehet véges számés ebben az esetben a nem megfelelő integrált konvergensnek nevezzük. A terület lehet végtelen is, és ebben az esetben a nem megfelelő integrált divergensnek nevezzük.

Egy integrál határértékének használata a nem megfelelő integrál helyett. A nem megfelelő integrál kiértékeléséhez a határozott integrál határértékét kell használni. Ha ez a határ létezik, és véges (nem egyenlő a végtelennel), akkor a nem megfelelő integrált konvergensnek, egyébként pedig divergensnek nevezzük. Az, hogy egy változó milyen mértékben hajlik a határjel alá, attól függ, hogy az első vagy a második típusú nem megfelelő integrállal van-e dolgunk. Ezt most derítsük ki.

Az első típusú helytelen integrálok - végtelen határokkal és konvergenciájukkal

Nem megfelelő integrálok végtelen felső határral

Tehát egy nem megfelelő integrál írása abban különbözik a szokásos határozott integráltól, hogy az integráció felső határa végtelen.

Meghatározás. Nem megfelelő integrál végtelen felső integrációs határral folyamatos funkció f(x) közötti intervallumban a hogy ∞ ennek a függvénynek az integráljának határát az integráció felső határával nevezzük b és az integráció alsó határa a feltéve, hogy az integráció felső határa korlátlanul nő, azaz

.

Ha ez a határ létezik, és nem a végtelen, hanem valamilyen számmal egyenlő, akkor a nem megfelelő integrált konvergensnek nevezzük, és azt a számot veszik értéknek, amellyel a határ egyenlő. Egyébként a nem megfelelő integrált divergensnek nevezzükés semmi értelmet nem tulajdonítanak neki.

Példa 1. Számítsa ki a nem megfelelő integrált(ha összefolyik).

Megoldás. A nem megfelelő integrál definíciója alapján azt találjuk

Mivel a határ létezik és egyenlő 1-gyel, akkor ez helytelen integrál konvergálés egyenlő 1-gyel.

A következő példában az integrandus majdnem ugyanaz, mint az 1. példában, csak az x fok nem kettő, hanem az alfa betű, és a feladat a nem megfelelő integrál tanulmányozása a konvergenciához. Vagyis a kérdés megválaszolásra vár: milyen alfa-értékeknél konvergál ez a helytelen integrál, és milyen értékeknél tér el?

2. példa Vizsgálja meg a nem megfelelő integrált a konvergenciára(az integráció alsó határa nagyobb, mint nulla).

Megoldás. Akkor először tegyük fel, hogy

Az eredményül kapott kifejezésben a következő határértékre lépünk:

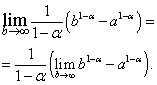
Könnyen belátható, hogy a jobb oldali határ létezik és egyenlő nullával, mikor , azaz , és nem létezik, mikor , azaz .

Az első esetben, amikor . Ha, akkor és nem létezik.

Tanulmányunk következtetése a következő: ez helytelen integrál konvergálés eltér at .

A Newton-Leibniz képlet alkalmazása a vizsgált nem megfelelő integrál típusára , levezetheti a következő képletet, amely nagyon hasonlít hozzá:

.

Ez általánosított képlet Newton-Leibniz.

3. példa: Számítsa ki a nem megfelelő integrált(ha összefolyik).

Ennek az integrálnak a határa létezik:

A második integrál, amely az eredeti integrált kifejező összeget alkotja:

Ennek az integrálnak a határa is létezik:

.

Megtaláljuk két integrál összegét, ami egyben az eredeti nem megfelelő integrál értéke is két végtelen határral:

A második típusú helytelen integrálok - korlátlan függvényekből és konvergenciájukból

Legyen a függvény f(x) tól származó szegmensen adott a hogy b és korlátlan. Tegyük fel, hogy a függvény a pontban a végtelenbe megy b , míg a szakasz összes többi pontján folytonos.

Meghatározás. Egy függvény nem megfelelő integrálja f(x) től származó szegmensen a hogy b ennek a függvénynek az integráljának határát az integráció felső határával nevezzük c , ha a törekvés során c To b a függvény korlátozás nélkül növekszik, és a ponton x = b funkció nincs definiálva, azaz

.

Ha ez a határ létezik, akkor a második típusú nem megfelelő integrált konvergensnek, ellenkező esetben divergensnek nevezzük.

A Newton-Leibniz képlet segítségével levezetjük.